Note:
- Although the document is very comprehensive, this article is mainly for quick completion in one day, so please forgive me for the shortcomings.
- The code is based on matlab terminal called by vscode/py 3.6
Basic mathematical operation and matrix operation
Basic grammar
variable
- No declaration required
- Assign a value to a variable with =
Variable name
- Variable names are case sensitive (I don't know if it's because of windows)
- Variable names can only be [0~9,a~z,A~z,] And the variable name cannot start with a number
- Reserved variables are not suitable for variable names
- Use the iskeyword command to view program keywords, which are not allowed to be used as variable names
variable | significance |
|---|---|
ans | The result of the previous sentence operation |
i,j | Complex operator, (note here) |
Inf | infinite |
eps | Floating point relative precision, i.e. the distance from 1.0 to the next floating point number (the value is 2.2204e-16) |
NaN | Non numeric |
pi | PI |
Variable names should not override built-in function names
In MATLAB, the calling priority of variable is higher than that of function, so the variable name should not overwrite the built-in function

For example:
cos = 'changqingaas'; cos(8) % disp(['ans is ', num2str(ans)]) clear; % If a function is overwritten by a variable name,Then call clear <Variable name>You can unbind the variable name on the function name cos(8) % disp(['ans is ', num2str(ans)])
Note: clear is a dangerous command, because if no parameters are added after the command, it means to clear all variables in the current workspace
Output:
ans =
'n'
ans =
-0.1455Variable type
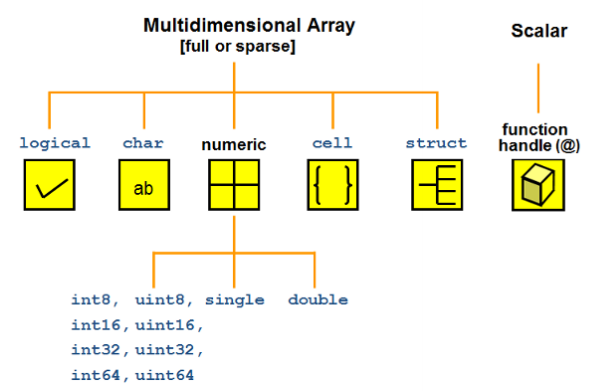
logical,char,numeric,cell,struct and their array or matrix
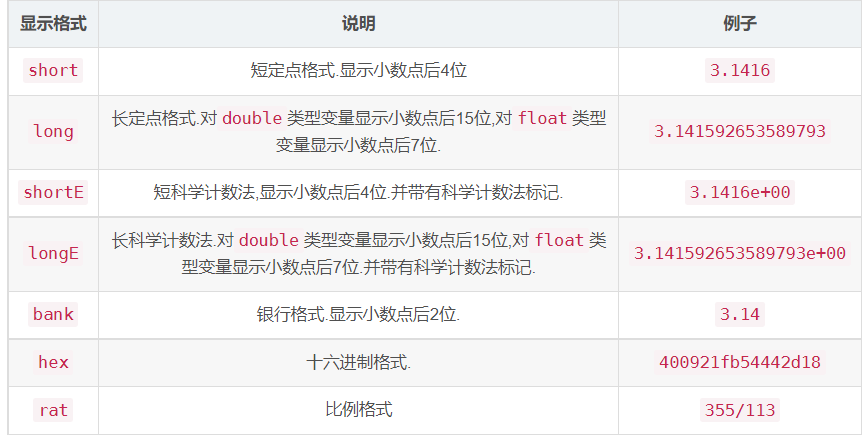
Display format of numeric variables
Numeric variable, which is stored in the form of double by default
You can change the display format of numeric variables through format < Display Format >
MATLAB command line
- Use end of line; Suppress output:
- Use after one line of command; Suppress the output, otherwise the operation result will be displayed on the terminal
- |Command | function | operation result| | -—- | --------------- | --------------- | |clc | clear the output of the terminal || |Clear | clear all variables in the current workspace by default || |who | displays all variables in the workspace in a simplified format | your variables are: ans | |whos | display all variables in the workspace in complex format | name size bytes class attributes ans 1x1 8 double | |which | view the location of the source code file of the built-in function. Combined with the edit command, you can view the source code of the built-in function|
Use MATLAB for digital operation
Calculate mathematical expressions using MATLAB
- After the mathematical expression is calculated, its value is stored in the variable ans
- log indicates ln
- exp(x) means e^x
MATLAB built-in mathematical function
- MATLAB built-in arithmetic operation function
- Basic operation:
- Plus: +, sum,cumsum,movsum
- Minus: -, diff
- Multiply by:. *, *, prod,cumprod
- Except:. /,. \, /\
- Power: ^^
- Modular operation: mod,rem,idivide,ceil,fix,floor,round
- Basic operation:
- MATLAB built-in trigonometric operation function
- Sine: sin,sind,sinpi,asin,asind,sinh,asinh
- Cosine: cos,cosd,cospi,acos,acosd,cosh,acosh
- Tangent: tan,tand,atan,atand,atan2,atan2d,tanh,atanh
- Cosecant: csc,cscd,acsc,acscd,csch,acsch
- Secant: sec,secd,asec,asecd,sech,asech
- cot,cotd,acot,acotd,coth,acoth
- Bevel: hypot
- Conversion: deg2rad,rad2deg,cart2pol,cart2sph,pol2cart,sph2cart
- Built in exponential logarithm function of MATLAB:
- exp,expm1,log,log10,log1p,log2,nextpow2,nthroot,pow2,reallog,realpow,realsqrt,sqr
- Complex functions built in MATLAB:
- abs,angle,complex,conj,cplxpair,i,imag,isreal,j,real,sign,unwrap
Matrix operation using MATLAB
Definition matrix
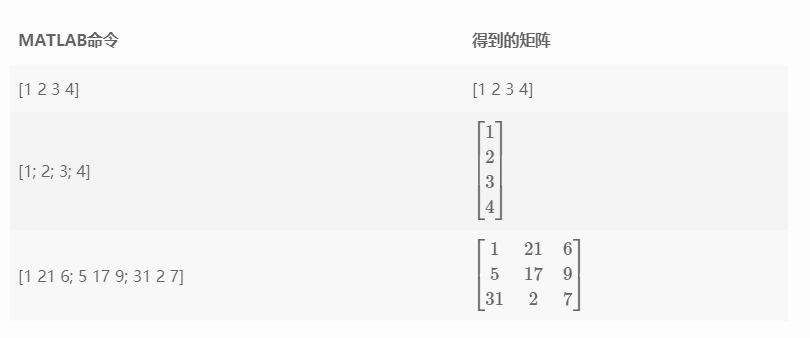
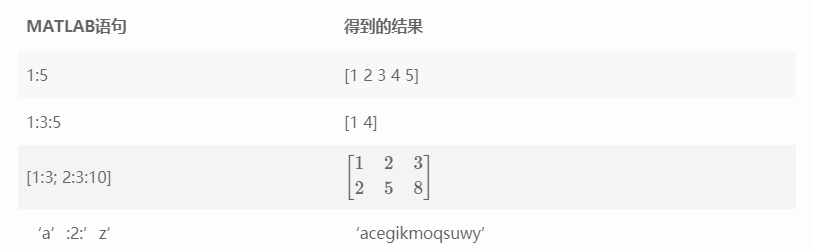
Input matrix to terminal
In MATLAB, use [] to enclose the matrix content to be input, use spaces or commas to separate variables in the line, and use; Separate each line
Create vectors using colon operators
Using colon operator: you can create a long vector with the following syntax:

For example:
Define special matrix
command | Results obtained |
|---|---|
eye(n) | Get an n × Identity matrix of n |
zeros(n1, n2) | Get an n1 × All zero matrix of N 2 |
ones(n1, n2) | Get an n1 × All 1 matrix of N 2 |
diag(vector) | Get a diagonal matrix with the content in the vector vector as the diagonal |
Index of matrix
- The matrix in MATLAB is stored in column order And the index subscript starts from 1
- There are two indexing methods for matrices: one-dimensional indexing and two-dimensional indexing For a general matrix, the index order is as follows: \ begin{bmatrix} 1 or (1,1) & 4 or (1,2) & 7 or (1,3) \ \ 2 or (2,1) & 5 or (2,2) & 8 or (2,3) \ \ 3 or (3,1) & 6 or (3,2) & 9 or (3,3) \ end {bMatrix}
- The index of matrix can use colon:, which means to select all rows or columns
- The index of the matrix can be one or two vectors, representing all rows or columns in the selected vector| The result of the original matrix | index | ------------------------------------------------------------------------------------------------------| \ begin {bmatrix} 1 & 2 & 3 \ 4 & 5 & 6\ 7 & 8 & 9 \end{bmatrix}\begin{bmatrix} 1 & 2 & 3 \ 4 & 5 & 6\ 7 & 8 & 9 \end{bmatrix}\begin{bmatrix} 1 & 2 & 3 \ 4 & 5 & 6\ 7 & 8 & 9 \end{bmatrix}\begin{bmatrix} 1 & 4 \ 7 & 2\end{bmatrix}\begin{bmatrix} 1 & 2 & 3 \ 4 & 5 & 6\ 7 & 8 & 9 \end{bmatrix}\begin{bmatrix} 1 & 2 & 3 \ 4 & 5 & 6\ 7 & 8 & 9 \end {bmatrix}\begin{bmatrix} 1 & 2 & 3 \ 4 & 5 & 6 \end{bmatrix}\begin{bmatrix} 1 & 2 & 3 \ 4 & 5 & 6\ 7 & 8 & 9 \end{bmatrix}\begin{bmatrix} 1 & 2 \ 7 & 8 \end{bmatrix}
Matrix operation
Operator of operation matrix
operator | operation | form | example |
|---|---|---|---|
+ | Matrix and vector addition | A+b | [6 3] + 2 = [8 5] |
- | Matrix and vector subtraction | A-b | [6 3] - 2 = [4 1] |
+ | The matrix is added to the corresponding position of the matrix | A+B | [6 3] + [4 8] = [10 11] |
- | The matrix is subtracted from the corresponding position of the matrix | A-B | [6 3] - [4 8] = [2 -5] |
* | Matrix Matrix Multiplication | A*B | [6 3] * [4 8]' = 48 |
.* | The matrix is multiplied by the corresponding position of the matrix | A.*B | [6 3] * [4 8] = [24 24] |
/ | Matrix and matrix right division (equivalent to A*inv(B)) | A/B | [6 3] / [4 8] = 0.6 |
\ | Matrix and matrix left division (equivalent to inv(A)*B) | A\B | [6 3] / [4 8] = [0.06667 1.3333; 0 0] |
./ | Right division of matrix and corresponding position of matrix | A./B | [6 3] ./ [4 8] = [1.5 0.375] |
.\ | Left division of matrix and corresponding position of matrix | A.\B | [6 3] .\ [4 8] = [0.6667 2.6667] |
^ | Matrix and vector power | A^b | [1 2; 3 4]^3 = [37 54; 81 118] |
.^ | Matrix and matrix corresponding position power | A.^B | [1 2; 3 4].^[1 2; 3 4] = [1 4; 27 256] |
Function of operation matrix
For the following matrix
A=\begin{bmatrix} 1 & 2 & 3 \\ 0 & 5 & 6 \\ 7 & 0 & 9 \end{bmatrix}
Operate to demonstrate common functions of the operation matrix
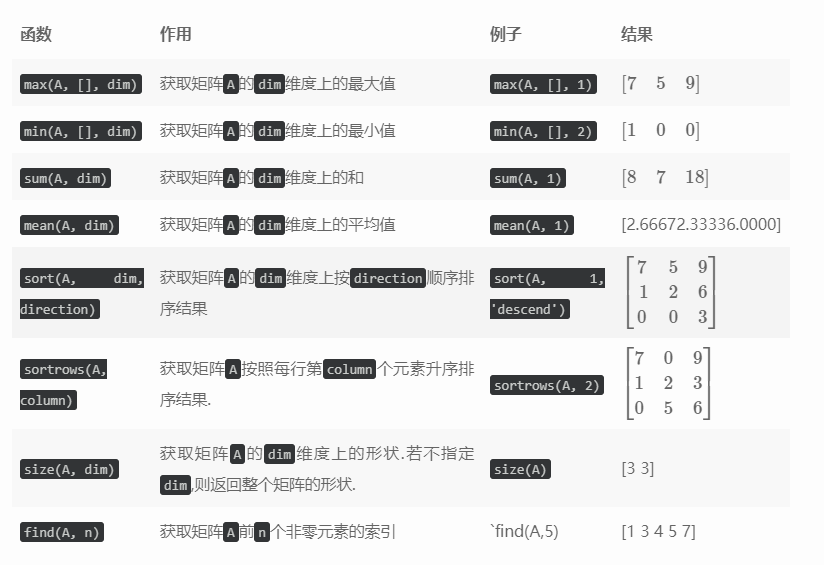
For the above functions, all parameters are optional except the first parameter
Structured programming and function definition
Structured programming
Process control statements and logical operators
Process control statement | effect |
|---|---|
if, elseif, else | if clause is true, execute the statement |
switch, case, otherwise | Judge which clause to execute according to the content of the switch statement |
while | Repeat the clause until the condition in while is false |
for | Execute clause a fixed number of times |
try, catch | Execute the clause and catch exceptions during execution |
break | Jump out of loop |
continue | Go directly to the next cycle |
end | End clause |
pause | Suspend program |
return | Return to the calling function |
All the above loops and conditional statements should be closed with end at the end
MATLAB also has the following logical operators:
operator | significance | ||
|---|---|---|---|
== | be equal to | ||
~= | Not equal to | ||
&& | And (support logic short circuit) | ||
` | ` | Or (support logic short circuit) |
Example of process control statement
if statement:
if condition1 statement1 elseif condition2 statement2 else statement3 end
switch Statements
switch expression
case value1
statement1
case value2
statement2
otherwise
statement
endwhile statement
while expression statement end
for statement
for variable = start:increment:end commands end
break statement
x = 2; k = 0; error = inf;
error_threshold = 1e-32;
while error > error_threshold
if k > 100
break
end
x = x - sin(x) / cos(x);
error = abs(x - pi);
k = k + 1;
endTry to pre allocate memory space when using circular statements
Problems needing attention when writing scripts
A statement should be added at the beginning of the script to empty the workspace
At the beginning of each script, the following statement should be added to empty the workspace cache and traces of previous program operation:
clear all % Clear variables in workspace memory close all % Close the image drawn by the previous program clc % Output of the program at the terminal before emptying
Semicolon shall be added after operation and assignment statement; Suppress output
Semicolons should be added to all operations and assignment statements; Suppress the output. If you need to output a variable to the terminal, you should call the disp method
Use ellipsis Splicing multiline statements
In MATLAB, ellipsis Multiple lines of statements can be spliced into one line, and the flexible use of this statement can improve the readability of the code
function
Similar to scripts, functions can be stored in function names m file can also be defined in memory in the form of function handle
View built-in functions
We can use the which command to view the location of the source code file of the built-in function. Combined with the edit command, we can view the source code of the built-in function
Run the following statement to open the source file of MATLAB's built-in mean function:
edit(which('mean.m'))
In function name m file form definition function
The format of the function defined in the MATLAB file is as follows:
function [Output variable name] = Function name(Enter variable name) % Documentation of functions function code
- Function is a keyword that declares that a function is saved in the file
- Input variables and output variables are not necessary. Functions can have neither input variables nor output variables
- Function name should be the same as m file name is the same and does not contain special characters (preferably Chinese)
MATLAB built-in function parameters
Function parameters | significance |
|---|---|
imputname | Enter a list of variable names |
mfilename | Function source code file name |
nargin | Number of input variables |
nargout | Number of output variables |
varargin | Variable length input parameter list |
varargout | Variable length output parameter list |
MATLAB does not provide syntax for specifying default parameter values and function overloading in other high-level languages, but the flexible use of the above built-in function parameters can realize specifying default parameter values and method overloading to a certain extent:
MATLAB function definition example 1
The surface program is used to calculate the displacement in the free fall movement: x = x_{0} + v_{0}t + \frac{1}{2} g t^2
function x = freebody(x0,v0,t) % calculation of free falling % x0: initial displacement in m % v0: initial velocity in m/sec % t: the elapsed time in sec % x: the depth of falling in m x = x0 + v0.*t + 1/2*9.8*t.*t;
This function demonstrates a MATLAB programming skill: try to use it when calculating multiplication* Not *, because the former is available not only when the parameter t is scalar, but also when the variable t is vector or matrix
freebody(0, 0, 2) % Get 19.6000 freebody(0, 0, [0 1 2 3]) % obtain [0 4.9000 19.6000 44.1000] freebody(0, 0, [0 1; 2 3]) % obtain [0 4.9000; 19.6000 44.1000]
MATLAB function definition example 2
The following function realizes the conversion from Fahrenheit temperature to Celsius temperature. This function can identify the number of input samples to be converted. When the number of input samples to be converted is 0, exit the function
function F2C()
while 1
F_degree = input('tempreature in Fahrenheit: ', 's');
F_degree = str2num(F_degree);
if isempty(F_degree)
return
end
C_degree = (F_degree-32)*5/9;
disp(['tempreature in Celsius: ' num2str(C_degree)])
end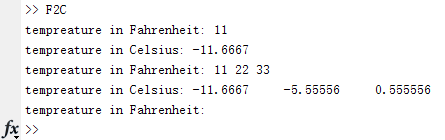
Define a function as a function handle
We can also define a function in the form of a function handle, which is closer to the mathematical function definition. Its syntax is as follows:
Function handle = @(Input variable) Output variable
This method can be called directly through the function handle
f = @(x) exp(-2*x); x = 0:0.1:2; plot(x, f(x));
Data type and file reading and writing
data type
The main data types in MATLAB are as follows:
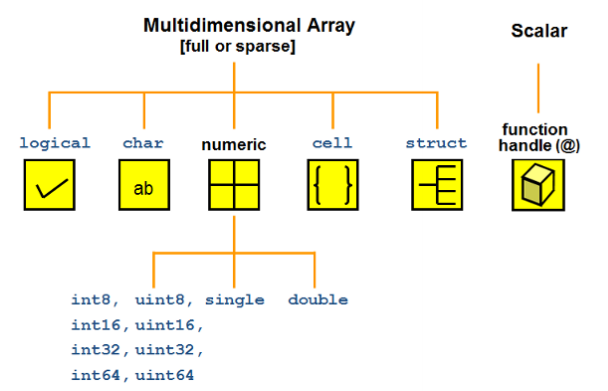
Numeric type
The numerical types supported by MATLAB are shown in the following table:
value type | describe |
|---|---|
double | Double precision floating point number |
single | Single-precision floating-point |
int8 | 8-bit signed integer |
int16 | 16 bit signed integer |
int32 | 32-bit signed integer |
int64 | 64 bit signed integer |
uint8 | 8-bit unsigned integer |
uint16 | 16 bit unsigned integer |
uint32 | 32-bit unsigned integer |
uint64 | 64 bit unsigned integer |
The value type of. double can be converted to the value type of other variables in MATLAB by default
n = 3; class(n) n = int8(3); class(n)
Output:
ans =
'double'
ans =
'int8'String type (char)
In MATLAB, the string type is defined by a pair of single quotation marks' wrapping a text Standard ASCII characters can be converted to corresponding ASCII codes
s1 = 'h'; uint16(s1) % Get 104
Strings are stored in memory in the form of character matrix, which can be indexed and assigned:
str1 = 'hello'; str2 = 'world'; str3 = [str1 str2]; size(str3) % obtain [1 10] str4 = [str1; str2]; size(str4) % obtain [2 5]
str = 'aardvark'; 'a' == str % obtain [1 1 0 0 0 1 0 0] str(str == 'a') = 'Z' % obtain 'ZZrdvZrk'
Structure
In MATLAB, the structure is a key value pair
Basic use of structure
- Similar to most programming languages, MATLAB uses To access fields in the structure:
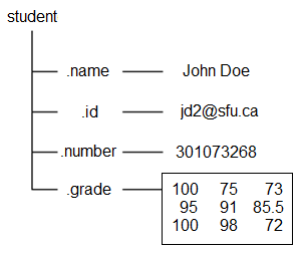
student.name = 'John Doe';
student.id = 'jdo2@sfu.ca';
student.number = 301073268;
student.grade = [100, 75, 73; ...
95, 91, 85.5; ...
100, 98, 72];
studentUsing subscript expressions on the structure list can expand or reduce the structure list
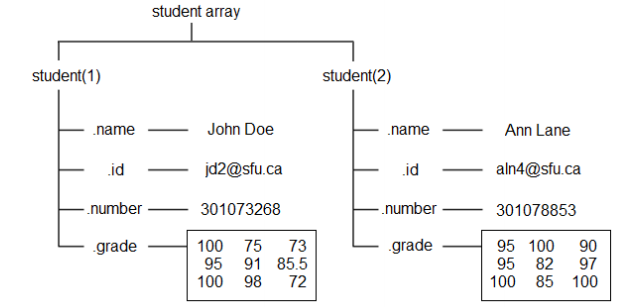
student.name = 'John Doe'; student.id = 'jdo2@sfu.ca'; student.number = 301073268; student.grade = [100, 75, 73; 95, 91, 85.5; 100, 98, 72]; student student(2).name = 'Ann Lane'; student(2).id = 'aln4@sfu.ca'; student(2).number = 301078853; student(2).grade = [95 100 90; 95 82 97; 100 85 100]; student(1) = [] % delete student First item in the list
Structures can be cascaded, that is, the value of fields in structures can also be structures:
A = struct('data', [3 4 7; 8 0 1], ...
'nest', struct('testnum', 'Test 1', ...
'xdata', [4 2 8], ...
'ydata', [7 1 6]));
A(2).data = [9 3 2; 7 6 5];
A(2).nest.testnum = 'Test 2';
A(2).nest.xdata = [3 4 2];
A(2).nest.ydata = [5 0 9];
ACommon functions of structures
function | effect |
|---|---|
struct | Create structure |
struct2cell | Convert structure to cell array |
cell2struct | Convert a cell array to a structure |
isstruct | Judge whether a variable is a structure |
structfun | Apply a function to each field of the structure |
fieldnames | Gets all field names of the structure |
isfield | Determine whether the structure contains a field |
getfield | Gets the value of a field in the structure |
setfield | Assign a value to a field in the structure |
rmfield | Delete a field in a structure |
orderfields | Sort structure fields |
Cell array
In MATLAB, cell array is a data structure that can accommodate different types of elements, similar to the list in Python language
Basic use of cell array
Use {} to define a cell array like a matrix:
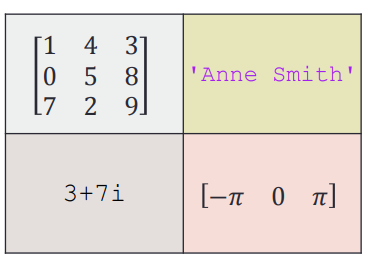
A = { [1 4 3; 0 5 8; 7 2 9] 'Anne Smith' ;...
3+7i -pi:pi:pi}A(1,1)={[1 4 3; 0 5 8; 7 2 9]};
A(1,2)={'Anne Smith'};
A(2,1)={3+7i};
A(2,2)={-pi:pi:pi};A{1,1}=[1 4 3; 0 5 8; 7 2 9];
A{1,2}='Anne Smith';
A{2,1}=3+7i;
A{2,2}=-pi:pi:pi;
AThe above three methods are equivalent. The second method uses unit index assignment and the third method uses content index assignment
- There are two ways to access data in a cell array: the cell index () and the content index {}
Because the subset of cell array is still cell array, it is necessary to indicate whether we want to access a sub cell array or the content in the corresponding area of cell array in the use of indexer content
- Using the cell index (), we get an array of sub cells
- Using the content index {}, we get the content in the corresponding area of the cell array
- Using the cell index (), we get an array of sub cells
Common functions of cell array
Common functions of cell array
function | effect |
|---|---|
cell | Create a cell array |
iscell | Determine whether a variable is a cell array |
cell2mat | Convert cell array to matrix |
cell2struct | Convert cell array to structure |
mat2cell | Converts an array to a cell array of the specified size |
num2cell | Converts an array to a cell array of the same size |
struct2cell | Convert structure to cell array |
celldisp | Recursively displays the contents of a cell array |
cellplot | Drawing cell structure in the form of array |
cellfun | Apply a function to each cell of the cell array |
The mat2cell function can specify the size of each cell in the cell array during conversion
a = magic(3) b = num2cell(a) % obtain % [8] [1] [6] % [3] [5] [7] % [4] [9] [2] c = mat2cell(a, [1 2], [2, 1]) % obtain % [1x2 double] [6] % [2x2 double] [2x1 double]
High dimensional cell array
A three-dimensional cell array can have three dimensions: row, column and layer When indexing cellular arrays, the order of priority from high to low is: row → column → layer

Using cat function, you can splice the cell array on the specified dimension
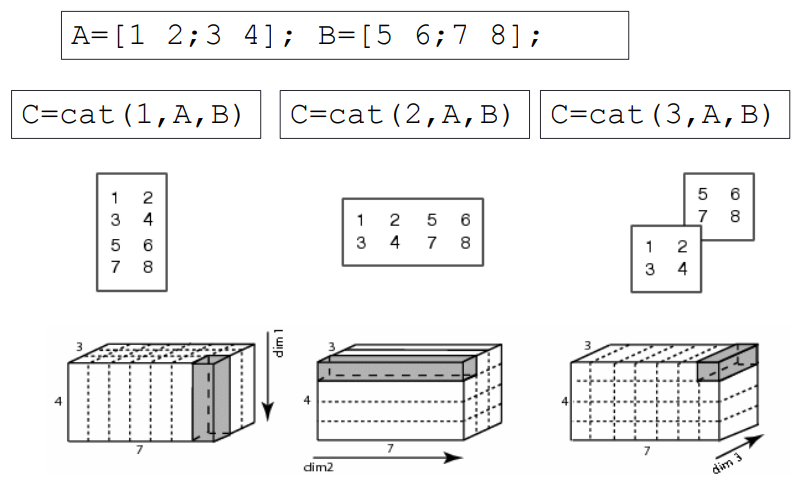
Function for judging variable data type
The following functions can judge the type of variables:
function | effect |
|---|---|
isinteger | Judge whether the input parameter is an integer array |
islogical | Judge whether the input parameter is a logical quantity array |
isnumeric | Judge whether the input parameter is a numeric array |
isreal | Judge whether the input parameter is a real array |
ischar | Judge whether the input parameter is a character array |
iscell | Judge whether the input parameter is a cell array |
isfloat | Determine whether the input array is a floating-point array |
ishandle | Determines whether the input array is a valid graphic handle |
isempty | Determine whether the input array is empty |
isprime | Determines which array elements are prime |
isnan | Determine which array elements are NaN |
isinf | Determines which array elements are Inf |
isequal | Determine whether the arrays are equal |
File reading and writing
The supported file types are as follows:
Document content | Extension | Functions to read files | Function to write to file |
|---|---|---|---|
MATLAB data | *.mat | load | save |
Excel table | *.xls,*.xlsx | xlsread | xlswrite |
Space delimited numbers | *.txt | load | save |
Read and write data in MATLAB format
The data in MATLAB workspace can be expressed in * The mat format is saved in a file Use the save function to save the data into the file, and use the load function to read the data from the file
- save
The syntax of the function is as follows:
- save(filename,variables) saves the variables into a file in binary form
- save(filename,variables,'-ascii') saves the variables to a file as text
- load
The syntax of the function is as follows:
- load(filename) reads data from a binary file
- load(filename,'-ascii') reads data from a text file
The parameters filename and variables are in string format. If the variables parameter is not specified, all variables in the current workspace will be stored in the file
Complex data formats, such as struct and cell, do not support storage in binary format
Reading and writing Excel tables
You can use xlsread and xlsworte functions to read and write Excel data. The syntax is as follows:
Syntax for reading Excel files: [num,txt,raw] = xlsread(filename,sheet,xlRange)
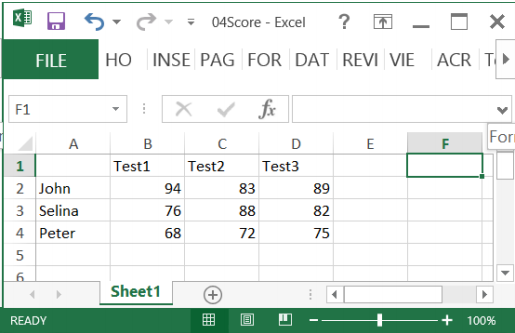
Score = xlsread('04Score.xlsx')
Score = xlsread('04Score.xlsx', 'B2:D4')
[Score Header] = xlsread('04Score.xlsx')Syntax for writing Excel: xlswrite(filename,A,sheet,xlRange)
M = mean(Score);
xlswrite('04Score.xlsx', M, 1, 'E2:E4');
xlswrite('04Score.xlsx', {'Mean'}, 1, 'E1');Basic drawing
Drawing and decoration of drawing lines
Use the plot() function to draw lines
In MATLAB, the plot() function is used to draw the plot line, and its syntax is:
plot(x,y,LineSpec)
LineSpec: line setting of drawing line. Three setting characters of specified line type, mark symbol and color form a string. The setting characters are not distinguished in order For details, please refer to Official documents.
Linetype symbol | Linetype setter | sign | Marker setter | colour | Color setter |
|---|---|---|---|---|---|
- | Solid line (default) | o | circle | y | yellow |
-- | Dotted line |
| plus | m | magenta |
: | Point line | * | asterisk | c | Turquoise blue |
-. | Dotted line | . | spot | r | gules |
x | Cross sign | g | green | ||
s | square | b | blue | ||
d | diamond | w | white | ||
^ | Upper triangle | k | black | ||
v | Lower triangle | ||||
> | Right triangle | ||||
< | Left triangle | ||||
p | Pentagonal | ||||
h | hexagon |
Note: the drawing method of matplotlib in Python is almost the same as here
Decorative drawing line
Use the legend() function to add a legend to the picture
Use the legend (label1,..., labeln) function to add a legend to the picture
x=0:0.5:4*pi;
y=sin(x); h=cos(x); w=1./(1+exp(-x)); g=(1/(2*pi*2)^0.5).*exp((-1.*(x-2*pi).^2)./(2*2^2));
plot(x,y,'bd-' ,x,h,'gp:',x,w,'ro-' ,x,g,'c^-'); % Draw multiple lines
legend('sin(x)','cos(x)','Sigmoid','Gauss function'); % Add legend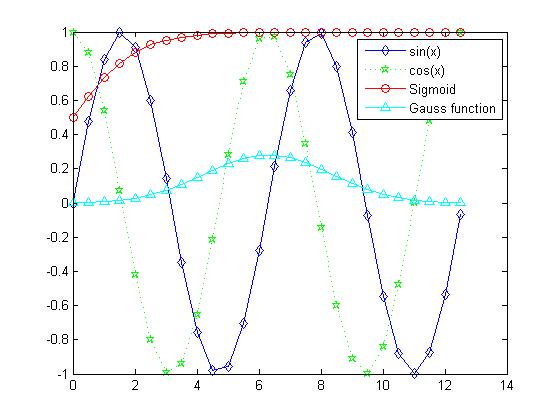
Use title() and * label() to add a title and label to the picture
x = 0:0.1:2*pi; y1 = sin(x); y2 = exp(-x);
plot(x, y1, '--*', x, y2, ':o');
xlabel('t = 0 to 2\pi');
ylabel('values of sin(t) and e^{-x}')
title('Function Plots of sin(t) and e^{-x}');
legend('sin(t)','e^{-x}');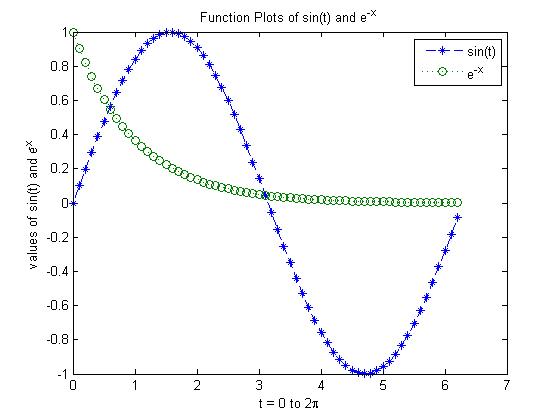
Use text() and annotation() to annotate the picture
x = linspace(0,3); y = x.^2.*sin(x); plot(x,y);
line([2,2],[0,2^2*sin(2)]);
str = '$$ \int_{0}^{2} x^2\sin(x) dx $$';
text(0.25,2.5,str,'Interpreter','latex');
annotation('arrow','X',[0.32,0.5],'Y',[0.6,0.4]); 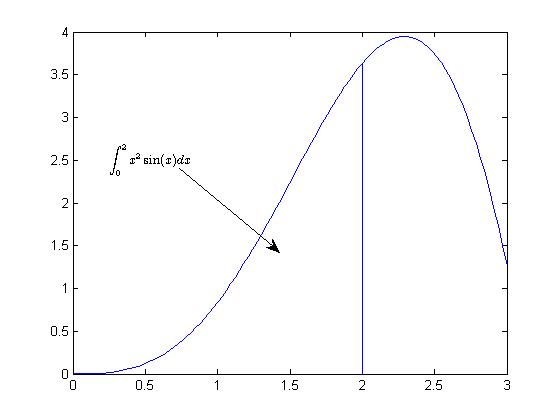
Control axes, borders and grids
command | effect |
|---|---|
grid on/off | Set mesh visibility |
box on/off | Set border visibility |
axis on/off | Set axis visibility |
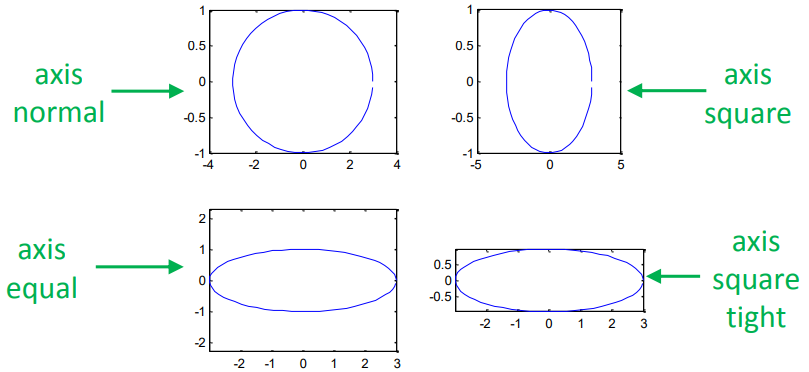
axis normal | Restore the default behavior and set the properties of frame aspect ratio mode and data aspect ratio mode to automatic |
axis square | Use coordinate axes of the same length to adjust the increment between data units accordingly |
axis equal | Use the same data unit length along each axis |
axis tight | Set the axis range to be equivalent to the data range, so that the axis frame closely surrounds the data |
The following example demonstrates the effect of the axis command:
t = 0:0.1:2*pi; x = 3*cos(t); y = sin(t); subplot(2, 2, 1); plot(x, y); axis normal subplot(2, 2, 2); plot(x, y); axis square subplot(2, 2, 3); plot(x, y); axis equal subplot(2, 2, 4); plot(x, y); axis equal tight
Draw multiple lines
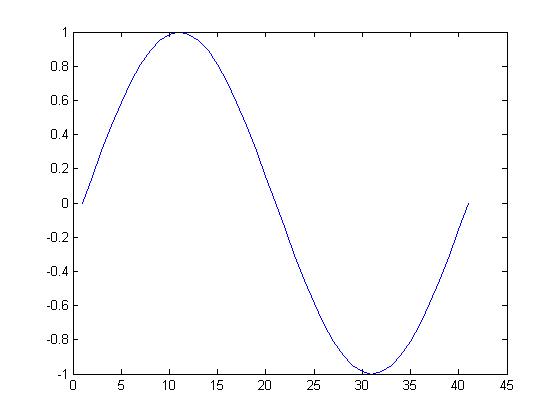
Draw multiple lines on one image
By default, each execution of the plot() function will clear the result of the last drawing, and multiple executions of plot() will only retain the last drawing
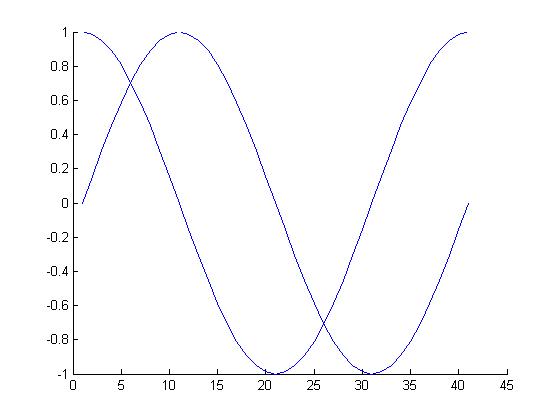
We can use hold on and hold off commands to control the refresh of the drawing area, so that multiple drawing results can be retained in the drawing area at the same time
hold on % Lift the brush,Start drawing a set of pictures plot(cos(0:pi/20:2*pi)); plot(sin(0:pi/20:2*pi)); hold off % Put down the brush,The group of pictures has been drawn
Draw multiple images in one window
subplot
Operation of drawing objects
In MATLAB, graphics are stored in memory in the form of objects, which can be operated by obtaining their graphic handles
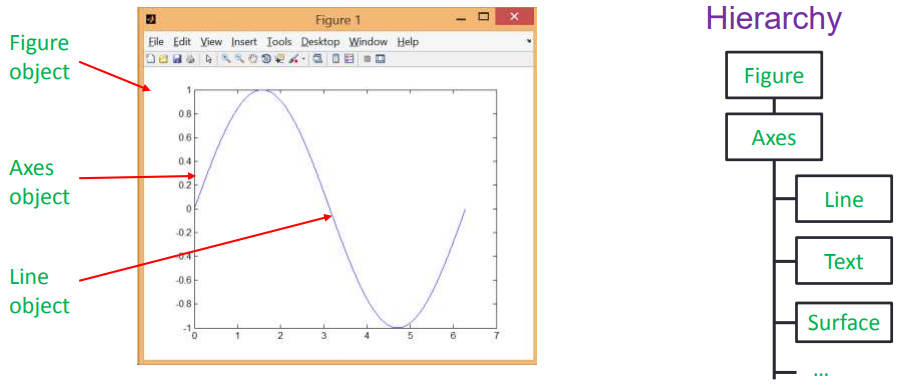
Get graph handle
A graphics handle is essentially a floating point number that uniquely identifies a graphics object The following functions are used to get the graphics handle
Function | Purpose |
|---|---|
gca() | Gets the handle of the current axis |
gcf() | Gets the handle of the current image |
allchild(handle_list) | Gets handles to all child objects of the object |
ancestor(h,type) | Gets the ancestor node of the object's nearest type |
delete(h) | Delete an object |
findall(handle_list) | Gets the descendants of the object |
All drawing functions also return a handle to the drawing object
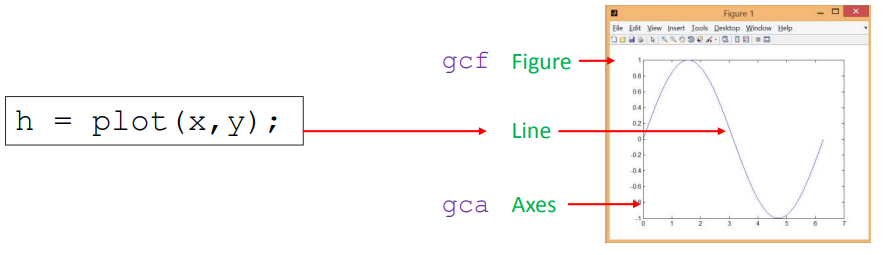
Manipulate drawing attributes through drawing handles
Use get() and set() functions to access and modify the properties of graphic objects visit Official documents You can view the properties of all drawing objects
- set(H,Name,Value)
- v = get(h,propertyName)

The following two examples demonstrate the use of graphic handles to manipulate graphic objects:
Change axis properties:
% First picture
set(gca, 'FontSize', 25);
% Second picture
set(gca, 'XTick', 0:pi/2:2*pi);
set(gca, 'XTickLabel', 0:90:360);
% The third picture
set(gca, 'FontName', 'symbol');
set(gca, 'XTickLabel', {'0', 'p/2', 'p', '3p/2', '2p'});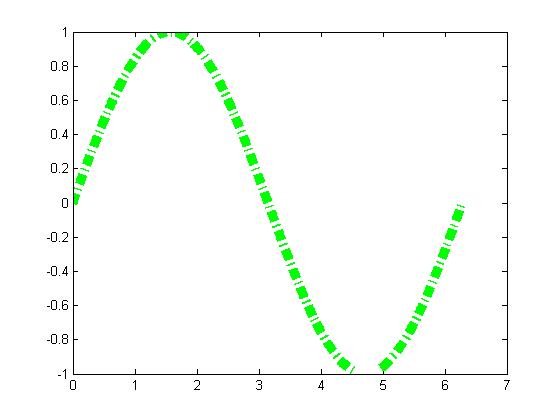
Change Linetype
h = plot(x,y); set(h, 'LineStyle','-.', ... 'LineWidth', 7.0, ... 'Color', 'g');

Save drawing to file
Use the saveas(fig,filename) command to save graphic objects to a file, where fig is the graphic handle and filname is the file name
saveas(gcf, 'myfigure.png')
Draw advanced charts
Two dimensional chart
Line chart
function | Graphic description |
|---|---|
loglog() | Both x-axis and y-axis take logarithmic coordinates |
semilogx() | The x-axis takes logarithmic coordinates and the y-axis takes linear coordinates |
semilogy() | The x-axis takes linear coordinates and the y-axis takes logarithmic coordinates |
plotyy() | Linear coordinate system with two sets of y axes |
ploar() | Polar coordinate system |
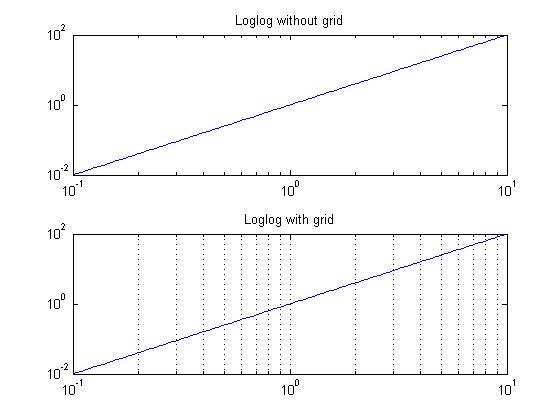
Logarithmic coordinate system line
The following example demonstrates a logarithmic coordinate system line:
x = logspace(-1,1,100); y = x.^2;
subplot(2,2,1);
plot(x,y);
title('Plot');
subplot(2,2,2);
semilogx(x,y);
title('Semilogx');
subplot(2,2,3);
semilogy(x,y);
title('Semilogy');
subplot(2,2,4);
loglog(x, y);
title('Loglog'); 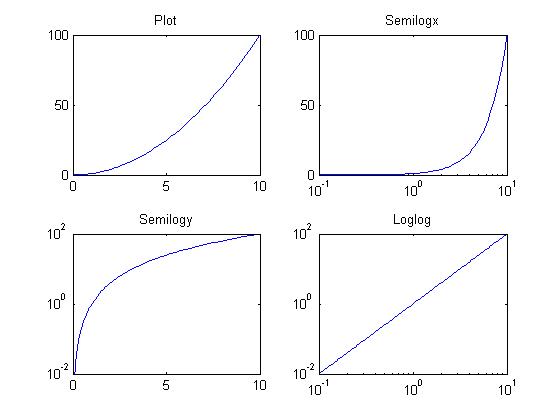
Logarithmic coordinate system can be added with grid to distinguish linear coordinate system from logarithmic coordinate system
set(gca, 'XGrid','on');
Double y-axis line
The return value of plotyy() is an array [ax,hlines1,hlines2], where:
- ax is a vector that holds handles to objects in two coordinate systems
- hlines1 and hlines2 are handles to two lines respectively
x = 0:0.01:20;
y1 = 200*exp(-0.05*x).*sin(x);
y2 = 0.8*exp(-0.5*x).*sin(10*x);
[AX,H1,H2] = plotyy(x,y1,x,y2);
set(get(AX(1),'Ylabel'),'String','Left Y-axis')
set(get(AX(2),'Ylabel'),'String','Right Y-axis')
title('Labeling plotyy');
set(H1,'LineStyle','--'); set(H2,'LineStyle',':');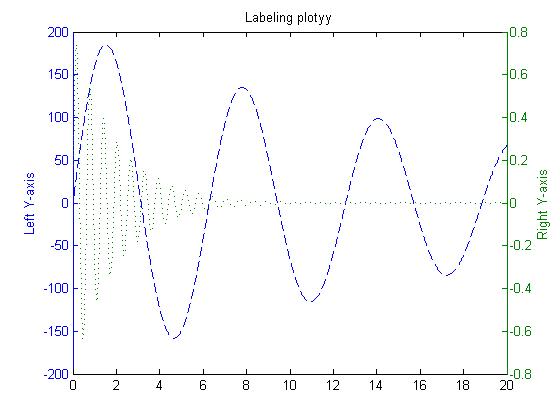
Statistical chart
function | Graphic description |
|---|---|
hist() | histogram |
bar() | Two dimensional histogram |
pie() | Pie chart |
stairs() | Stairs |
stem() | Needle diagram |
histogram
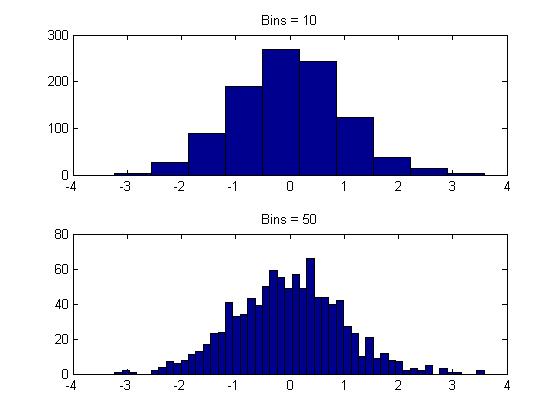
Histogram
Use bar() and bar3() functions to draw two-dimensional and three-dimensional histograms respectively
x = [1 2 5 4 8]; y = [x;1:5];
subplot(1,3,1); bar(x); title('A bargraph of vector x');
subplot(1,3,2); bar(y); title('A bargraph of vector y');
subplot(1,3,3); bar3(y); title('A 3D bargraph');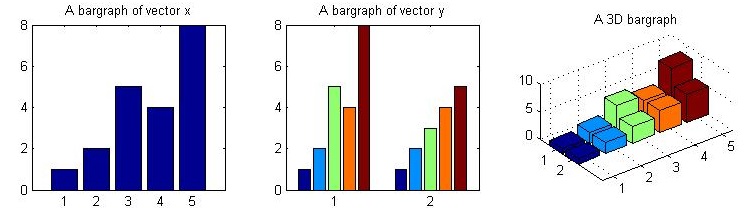
hist is mainly used to view the frequency distribution of variables, while bar is mainly used to view the statistical results of discrete quantities
Using the barh() function, you can draw a histogram arranged vertically
x = [1 2 5 4 8];
y = [x;1:5];
barh(y);
title('Horizontal');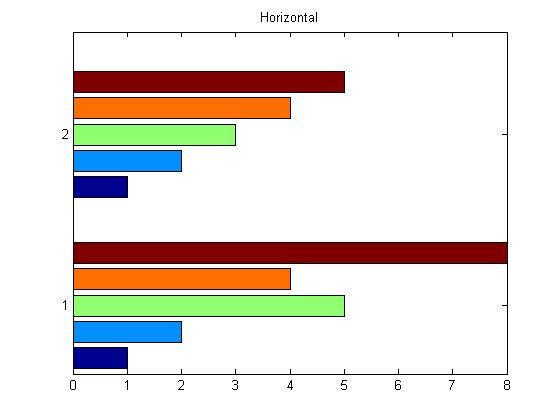
Passing the 'stack' parameter to bar() allows the histogram to be drawn in the form of a stack
x = [1 2 5 4 8];
y = [x;1:5];
bar(y,'stacked');
title('Stacked');
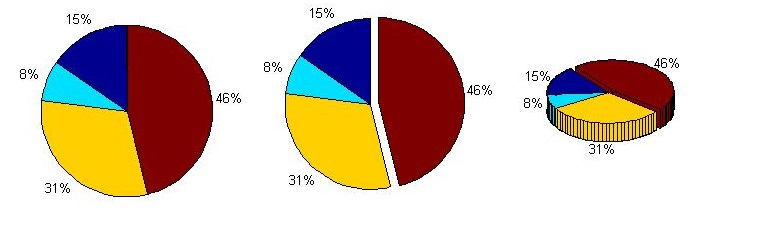
Pie chart
pie() and pie3() can be used to draw 2D and 3D pie charts A bool vector is passed in to indicate whether each sector is offset
a = [10 5 20 30]; subplot(1,3,1); pie(a); subplot(1,3,2); pie(a, [0,0,0,1]); subplot(1,3,3); pie3(a, [0,0,0,1]);
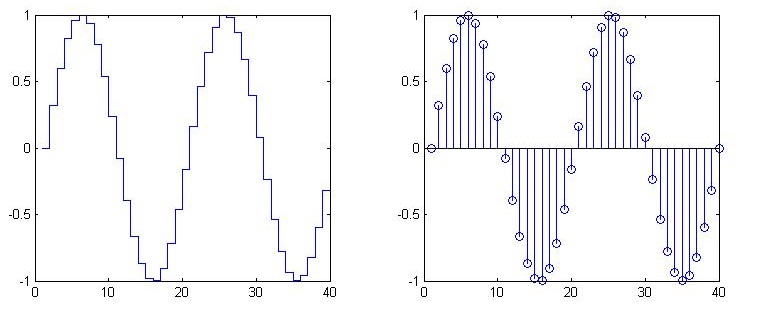
Ladder and needle charts: drawing discrete digital sequences
The stairs() and stem() functions are used to draw a ladder graph and a needle graph, respectively, to represent discrete digital sequences
x = linspace(0, 4*pi, 40); y = sin(x); subplot(1,2,1); stairs(y); subplot(1,2,2); stem(y);
Three dimensional chart
Convert 2D to 3D
In MATLAB, all graphs are three-dimensional graphs, and two-dimensional graphs are just a projection of three-dimensional graphs Click the Rotate 3D button in the graphics window to drag and drop the mouse to view the 3D view of the graphics
Convert 3D to 2D
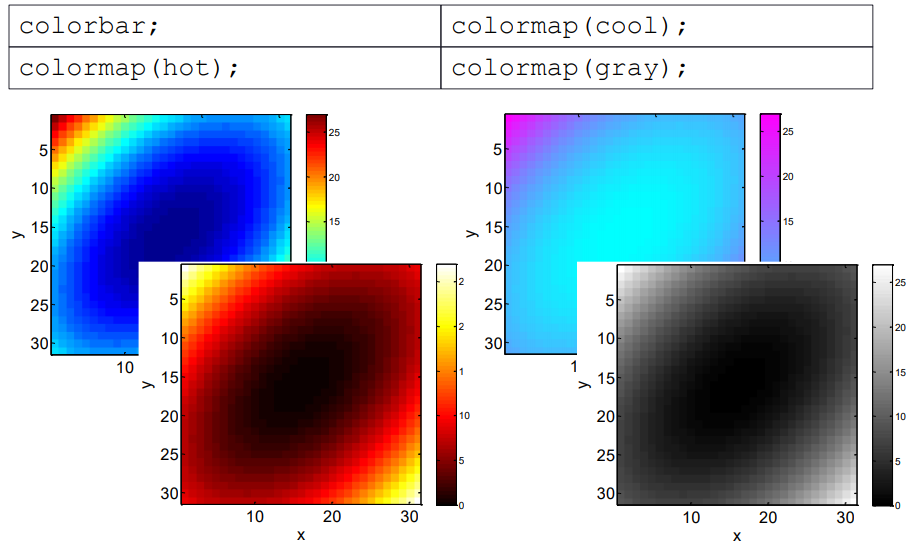
Use the imagesc() function to convert a three-dimensional view into a two-dimensional top view, and indicate the height by the color of the point
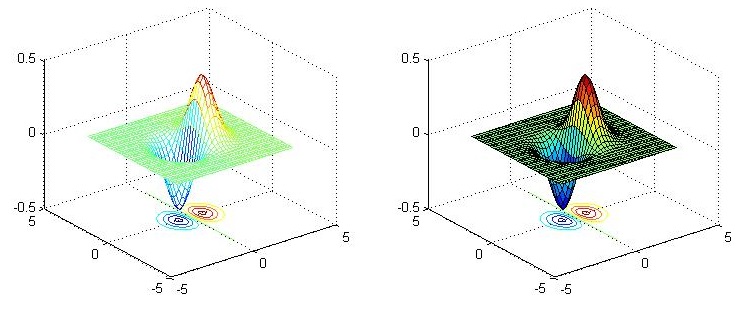
[x, y] = meshgrid(-3:.2:3,-3:.2:3); z = x.^2 + x.*y + y.^2; subplot(1, 2, 1) surf(x, y, z); subplot(1, 2, 2) imagesc(z);
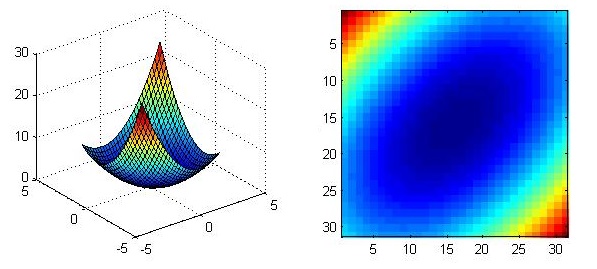
Use the colorbar command to add the legend of the corresponding relationship between color and height on the generated two-dimensional map, and use the colormap command to change the color scheme For details, please refer to Official documents
Drawing of three-dimensional drawing
Preparation before drawing 3D drawing
- Using meshgrid() to generate 2D mesh
The meshgrid() function expands the two input vectors by corresponding rows and columns to obtain two augmented matrices. The binary function can be applied to the matrix
x = -2:1:2; y = -2:1:2; [X,Y] = meshgrid(x,y) Z = X.^2 + Y.^2
Draw 3D lines
Use the plot3() function to draw a three-dimensional surface. The input should be three vectors
x=0:0.1:3*pi; z1=sin(x); z2=sin(2.*x); z3=sin(3.*x);
y1=zeros(size(x)); y3=ones(size(x)); y2=y3./2;
plot3(x,y1,z1,'r',x,y2,z2,'b',x,y3,z3,'g'); grid on;
xlabel('x-axis'); ylabel('y-axis'); zlabel('z-axis');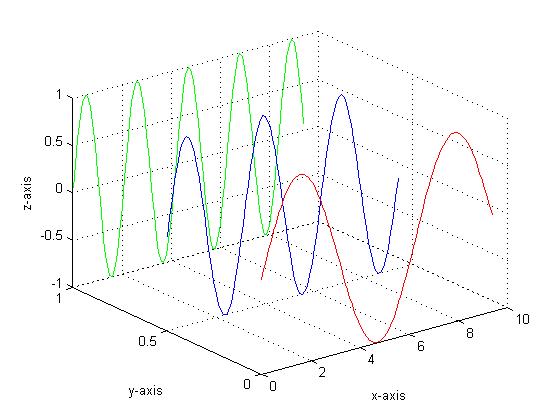
Draw 3D faces
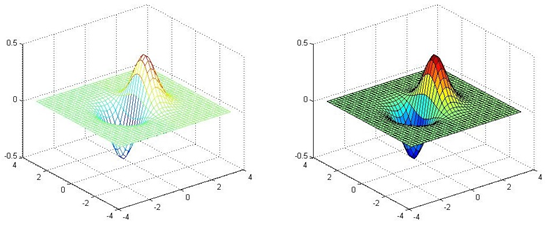
mesh() and surf() commands can be used to draw 3D faces. The former does not fill the mesh, while the latter does
x = -3.5:0.2:3.5; y = -3.5:0.2:3.5; [X,Y] = meshgrid(x,y); Z = X.*exp(-X.^2-Y.^2); subplot(1,2,1); mesh(X,Y,Z); subplot(1,2,2); surf(X,Y,Z);
Draw contours of 3D graphics
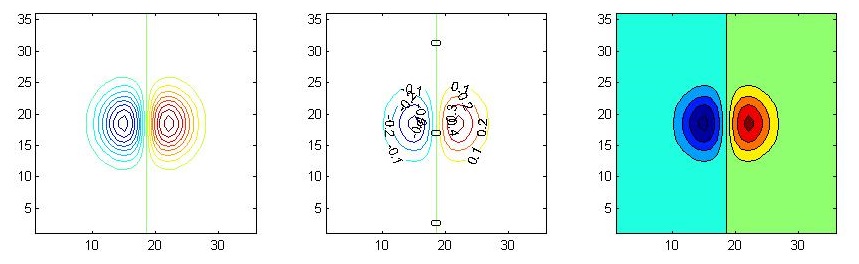
contour() and contour() functions can be used to draw contour lines of 3D graphics. The former does not fill the mesh, while the latter does
The details of the image can be changed by passing parameters or manipulating the graphics handle to the contour() function:
x = -3.5:0.2:3.5; y = -3.5:0.2:3.5; [X,Y] = meshgrid(x,y); Z = X.*exp(-X.^2-Y.^2); subplot(1,3,1); contour(Z,[-.45:.05:.45]); axis square; subplot(1,3,2); [C,h] = contour(Z); clabel(C,h); axis square; subplot(1,3,3); contourf(Z); axis square;
Using meshc() and surfc() functions, you can draw the contour lines of 3D graphics
x = -3.5:0.2:3.5; y = -3.5:0.2:3.5; [X,Y] = meshgrid(x,y); Z = X.*exp(-X.^2-Y.^2); subplot(1,2,1); meshc(X,Y,Z); subplot(1,2,2); surfc(X,Y,Z);
Draw 3D volume
Use the patch() function to draw a three - dimensional volume
v = [0 0 0; 1 0 0 ; 1 1 0; 0 1 0; 0.25 0.25 1; 0.75 0.25 1; 0.75 0.75 1; 0.25 0.75 1];
f = [1 2 3 4; 5 6 7 8; 1 2 6 5; 2 3 7 6; 3 4 8 7; 4 1 5 8];
subplot(1,2,1);
patch('Vertices', v, 'Faces', f, 'FaceVertexCData', hsv(6), 'FaceColor', 'flat');
view(3); axis square tight; grid on;
subplot(1,2,2);
patch('Vertices', v, 'Faces', f, 'FaceVertexCData', hsv(8), 'FaceColor','interp');
view(3); axis square tight; grid on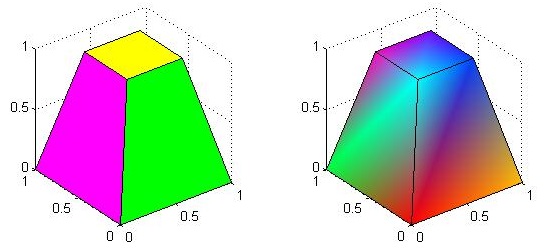
Perspective and lighting of three-dimensional drawings
Adjust Perspective
The view() function can be used to adjust the viewing angle. The view() function accepts two floating-point parameters, representing two azimuth azimuth and elevation
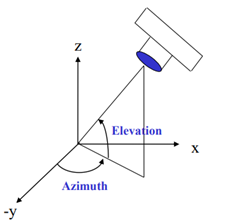
sphere(50); shading flat; material shiny; axis vis3d off; view(-45,20);

Symbolic operation
Create symbolic variable
Create symbolic numbers
Use the sym function to create symbolic numbers Using symbolic numbers can accurately save irrational numbers without error
sym(1/3) % Get 1/3 1/3 % Get 0.3333
Saving irrational numbers as symbolic numbers can avoid the error of converting them to floating-point numbers:
sin(sym(pi)) % Get 0 sin(pi) % Get 1.2246e-16
Create symbolic variable
sym and syms can be used to create symbolic variables. The difference is:
sym can only create one symbolic variable at a time, while syms can create multiple symbolic variables at a time
syms a % sym The command can only create one symbolic variable syms b c d % syms Command can create multiple symbolic variables
If the specified symbolic variable already exists, sym will not keep its original value, but syms will clear its value
syms x y f = x+y; % Implicitly create symbolic variables f sym f % Do not empty variables f Original value,Namely f = x + y
syms x y f = x+y; % Implicitly create symbolic variables f syms f % Empty variable f Original value,Namely f = f
Using sym, you can create a symbolic variable matrix
A = sym('a', [2 5]) % Create a 2*5 Symbolic variable matrix
whosThe output is as follows:
A = [ a1_1, a1_2, a1_3, a1_4, a1_5] [ a2_1, a2_2, a2_3, a2_4, a2_5] Name Size Bytes Class Attributes A 2x5 112 sym
Using sym and syms together, you can quickly create a series of variables with subscripts
clear all
syms(sym('a', [1 5]))
whosThe output is as follows:
Name Size Bytes Class Attributes a1 1x1 8 sym a2 1x1 8 sym a3 1x1 8 sym a4 1x1 8 sym a5 1x1 8 sym
Symbolic operation
Simplification and substitution of symbolic expressions
Simplification of symbolic expressions
Use the simplify() function to simplify symbolic expressions
syms x a b c simplify(sin(x)^2 + cos(x)^2); % Get 1 simplify(exp(c*log(sqrt(a+b)))); % obtain (a + b)^(c/2)
The standard of expression simplification is uncertain. The following three functions simplify expressions according to different standards:
The expand() function expands the expression
syms x f = (x ^2- 1)*(x^4 + x^3 + x^2 + x + 1)*(x^4 - x^3 + x^2 - x + 1); expand(f); % obtain x^10 - 1
The factor() function can decompose a factor
syms x g = x^3 + 6*x^2 + 11*x + 6; factor(g); % obtain (x + 3)*(x + 2)*(x + 1)
The horner() function can change polynomials into nested forms
syms x h = x^5 + x^4 + x^3 + x^2 + x; horner(h); % obtain x*(x*(x*(x*(x + 1) + 1) + 1) + 1)
Substitution of symbolic expressions
Use the sub(expr, old, new) function to replace old in the symbolic expression expr with new
syms x y f = x^2*y + 5*x*sqrt(y); subs(f, x, 3); % Get 9*y + 15*y^(1/2)
Find the analytical solution of the equation
Using solve(eqn,var) and solve(eqns,vars), the analytical solution of the equation can be obtained
Univariate solution of equation
Define an equation with = = and call the solve function to solve it (if the value to the right of the = = symbol is not specified, the default value to the right of the equation is 0.)
syms x eqn = x^3 - 6*x^2 == 6 - 11*x; solve(eqn); % obtain [1 2 3]
Solving multivariable equations
For multivariable equations, we need to specify which variable to solve
syms x y eqn = [6*x^2 - 6*x^2*y + x*y^2 - x*y + y^3 - y^2 == 0]; solve(eqn, y); % obtain [1, 2*x, -3*x]
Solving equations
The equations can be solved by passing the equations into the solve() function
syms u v eqns = [2*u + v == 0, u - v == 1]; S = solve(eqns,[u v]);
The solution of the equation can be indexed by variable name and can be substituted into other expressions
S.u; % Get 1/3 S.v; % obtain -2/3 subs(3*v + u, S); % obtain -3/5
Symbolic calculus
Find the limit
Use the limit(expr, var, a) function to find the limit of the symbolic expression expr when the variable var approaches A. add the parameter 'left' or 'right' to specify the left limit or right limit
syms x; expr = 1/x; limit(expr,x,0); % obtain NaN limit(expr,x,0,'left'); % obtain-Inf limit(expr,x,0,'right'); % obtain Inf
differential
Using diff(expr, var, n) function, the n-order differential of symbolic expression expr to variable var can be obtained
syms a b c x; expr = a*x^2 + b*x + c; diff(expr, a); % obtain x^2 diff(expr, b); % obtain x diff(expr, x); % obtain b + 2*a*x diff(expr, x, 2); % Get 2*a
integral
Using the int(expr, var) function, the indefinite integral of the symbolic expression expr to the variable var can be obtained Use the int(expr, var, [a, b]) function to specify the upper and lower limits for definite integral. A and B can be symbolic expressions
syms x a b expr = -2*x/(1+x^2)^2; int(expr, x); % Get 1/(x^2 + 1) int(expr, x, [1, 2]); % obtain -0.3 int(expr, x, [1, Inf]); % obtain -0.5 int(expr, x, [a, b]); % Get 1/(b^2 + 1) - 1/(a^2 + 1)
For some functions, MATLAB can't find their integral. At this time, MATLAB will return an unresolved integral form
syms x int(sin(sinh(x))); % An integral without solution,MATLAB return int(sin(sinh(x)),
Summation of series
Use symsum (expr, K, [a, b]) to calculate the sum of index k of series expr from a to B
syms k x symsum(k^2, k) % obtain k^3/3 - k^2/2 + k/6 symsum(k^2, k, [0 10]) % Get 385 symsum(x^k/factorial(k),k,1,Inf) % obtain exp(x) - 1
Taylor expansion
Use taylor(expr,var,a) to calculate the Taylor series of the expression expr at var=a
syms x taylor(exp(x)) % obtain x^5/120 + x^4/24 + x^3/6 + x^2/2 + x + 1 taylor(sin(x)) % obtain x^5/120 - x^3/6 + x taylor(cos(x)) % obtain x^4/24 - x^2/2 + 1
Draw image
You can draw images for symbolic expressions. The common drawing functions are as follows:
function | effect |
|---|---|
fplot() | Draws a 2D line image of a symbolic expression |
fplot3() | Draws a 3D line image of a symbolic expression |
ezpolar() | Draw a polar marking image of a symbolic expression |
fmesh() | Draw mesh face image |
fsurf() | Draw a colored face image |
fcontour() | Draw contour image |
fimplicit() | Draw an image of implicit functional relationship |
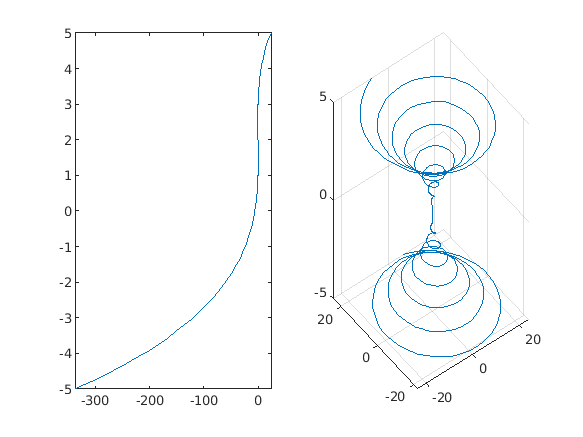
The following example shows the drawing of two-dimensional and three-dimensional line images
subplot(1, 2, 1) syms x f = x^3 - 6*x^2 + 11*x - 6; fplot(f, x) subplot(1, 2, 2) syms t fplot3(t^2*sin(10*t), t^2*cos(10*t), t)
The following example demonstrates the rendering of 3D faces
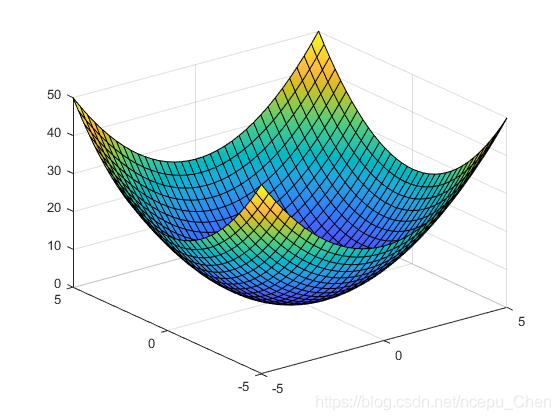
syms x y fsurf(x^2 + y^2)
The following example demonstrates the drawing of implicit function relation image
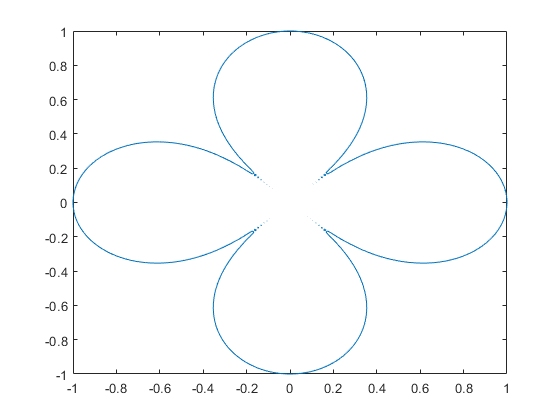
syms x y eqn = (x^2 + y^2)^4 == (x^2 - y^2)^2; fimplicit(eqn, [-1 1])
numerical calculation
Numerical operation of polynomials
Polynomial representation using MATLAB
Using vectors to represent polynomials
In MATLAB, polynomials can be represented by vectors. The elements in the vector are the coefficients of polynomials (descending order): the first is the coefficient of the highest order term of polynomials, and the last is the constant term
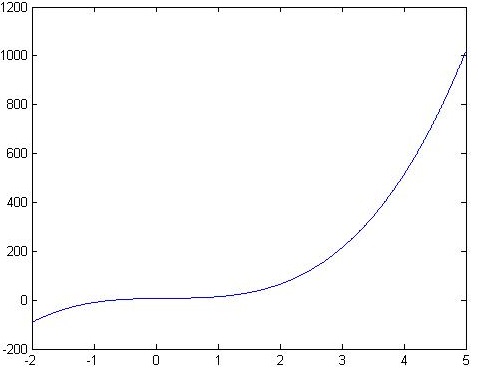
For example, polynomial: f(x) = x^3 - 2x - 5f(x)=x3−2x−5
It can be represented by vector p = [1 0 -2 -5]
Polynomial evaluation: polyval()
polyval(p, x) can be used to calculate the value of polynomial p at each point of X
a = [9,-5,3,7]; x = -2:0.01:5; f = polyval(a,x); plot(x,f);
Multiplication of Polynomials: conv()
Using conv(p1, p2) function, two vectors p1 and p2 can be convoluted and multiplied to calculate the multiplication of polynomials
For example, polynomial: f(x) = (x^2+1) (2x+7)f(x)=(x2+1)(2x+7)
The expanded polynomial can be obtained by using the conv() function:
p = conv([1 0 1], [2 7])
Get p = [2 7 2 7]
Numerical operation of polynomials
Factorization of Polynomials: roots()
The roots(p) function can be used to factorize the polynomial p, that is, to find the root of the expression value of 0
p = roots([1 -3.5 2.75 2.125 -3.875 1.25])
Get p = [2 -1, 1+0.5i, 1-0.5i, 0.5], representing x^5 -3.5 x^4 +2.75 x^3 + 2.125 x^2 + -3.875 x+1.25 = (x-2)(x+1)(x-1-0.5i)(x-1+0.5i)(x-0.5)x5 − 3.5x4+2.75x3+2.125x2 + − 3.875x+1.25=(x − 2)(x+1)(x − 1 − 0.5i)(x − 1+0.5i)(x − 0.5)
Differential of Polynomials: polyder()
The derivative of polynomial can be calculated by using polyder(p) function
For example, take the derivative of the following polynomial: f(x) = 5x^4 - 2x^2 + 1f(x)=5x4−2x2+1
p = polyder([5 0 -2 0 1]);
Get P = [200 - 40], which means that the derivative f '(x) = 20 x^3 - 4xf' (x)=20x3 − 4x
Integral of polynomial: polynomial ()
The polynomial (p, k) function can be used to calculate the integral of polynomial p, and the constant term of the integral result is set to k
For example, take the derivative of the following polynomial: f(x) = 5x^4 - 2x^2 + 1f(x)=5x4−2x2+1
p = polyint([5 0 -2 0 1], 3)
Get p = [1 0 -0.6667 0 1 3], which means the calculated integral \ int f(x) dx = x^5 -0.6667x^3 + x + 3 ∫ f(x)dx=x5 − 0.6667x3+x+3
Numerical operation of nonlinear expression
Root finding of equation (system) (fsolve)
Use fsolve(fun, x0) to find the root of nonlinear equations. Fun is the function handle of the equation to be solved, and x0 is the initial value
Find the solution of equation 1.2x+x\sin(x)+0.3=01.2x+xsin(x)+0.3=0 near x=0x=0
f2 = @(x) (1.2*x+x*sin(x)+0.3); fsolve(f2,0) % obtain -0.3500
Solving equations \begin{aligned} \left\{ \begin{aligned} e^{-e^{-(x_1+x_2)}} - x_2(1+x_1^2) = 0 \\ x_1 \cos x_2 + x_2 \sin x_1 - \frac{1}{2} = 0 \end{aligned} \right. \end{aligned}⎩⎪⎨⎪⎧e−e−(x1+x2)−x2(1+x12)=0x1cosx2+x2sinx1−21=0
Set the initial value as [0, 0] [0,0]
fun = @(x) [exp(-exp(-(x(1)+x(2))))-x(2)*(1+x(1)^2)...
x(1)*cos(x(2)) + x(2)*sin(x(1)) - 0.5]
x0 = [0,0];
x = fsolve(fun,x0) % obtain[0.3532 0.6061]Numerical differentiation
Difference: diff()
Use diff(X, n) to calculate the n-order difference of vector X, and N defaults to 1
x = [1 2 5 2 1]; diff(x); % obtain [1 3 -3 -1] diff(x,1); % obtain [1 3 -3 -1] diff(x,2); % obtain [2 -6 2]
Derivative: diff (y)/ diff(x)
Use the definition of derivative
You can calculate the approximate derivative of a function at a certain point
The following program calculates the values of the first and second derivatives of f(x) = x^3f(x)=x3
x = -2:0.005:2; y = x.^3;
m = diff(y)./diff(x); % Calculate the first derivative
m2 = diff(m)./diff(x(1:end-1)); % Calculate the second derivative
plot(x,y,x(1:end-1),m,x(1:end-2),m2);
xlabel('x'); ylabel('y');
legend('f(x) =x^3','f''(x)','f''''(x)', 4);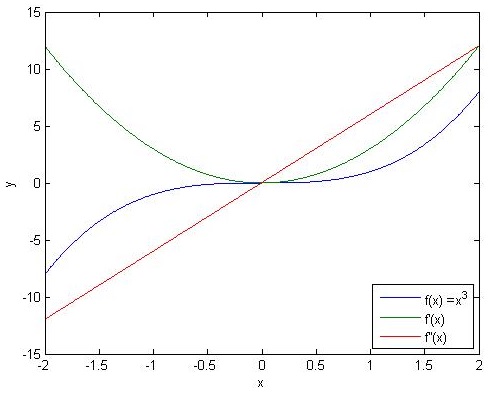
numerical integration
Numerical integration principle
There are three common algorithms used to calculate numerical integration: rectangular method, trapezoidal method and parabola method. They treat the graphics of differential interval as rectangle, trapezoid and parabola respectively to calculate the area
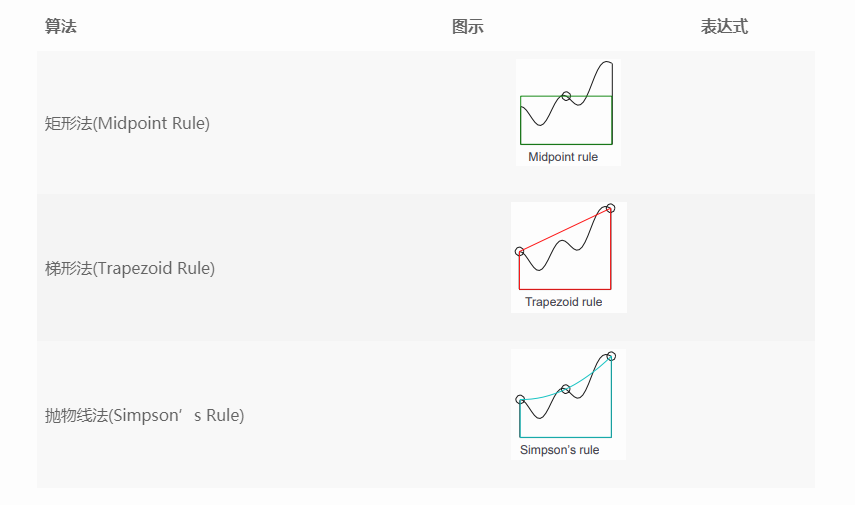
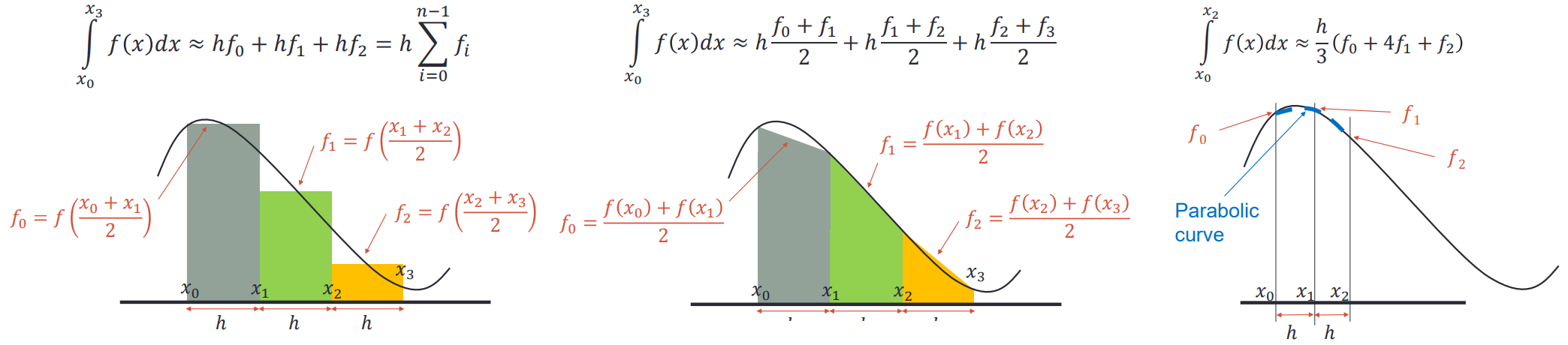
The following three methods are used to calculate the integral of f(x) = 4x^3f(x)=4x3 in the interval (0,2) (0,2)
h = 0.05; x = 0:h:2; % Use the rectangular method to calculate the approximate integral midpoint = (x(1:end-1)+x(2:end))./2; y = 4*midpoint.^3; s = sum(h*y) % Get 15.9950 % The trapezoidal method is used to calculate the approximate integral trapezoid = (y(1:end-1)+y(2:end))/2; s = h*sum(trapezoid) % Get 15.2246 % Numerical integration using parabolic method s = h/3*(y(1)+2*sum(y(3:2:end-2))+4*sum(y(2:2:end))+y(end)) % Get 15.8240
Numerical integration function: integral()
integral(),integral2(),integral3() perform single, double and triple integrals of the function from xmin to xmax respectively
Their first parameter should be a function handle. The following example demonstrates their usage:
Calculate \ int_0^2 \frac{1}{x^3-2x-5}∫02x3−2x−51
f = @(x) 1./(x.^3-2*x-5); integral(f,0,2) % obtain -0.4605
Calculate \ int_0^\pi \int_\pi^{2\pi} (y\sin(x) + x \cos(y)) dx dy∫0π∫π2π(ysin(x)+xcos(y))dxdy
f = @(x,y) y.*sin(x)+x.*cos(y); integral2(f,pi,2*pi,0,pi) % obtain -9.8696
Calculate \ int_{-1}^1 \int_0^1 \int_0^\pi (y\sin(x) + z \cos(y)) dx dy dz∫−11∫01∫0π(ysin(x)+zcos(y))dxdydz
f = @(x,y,z) y.*sin(x)+z.*cos(y); integral3(f,0,pi,0,1,-1,1)
Statistics and fitting
Statistics
Descriptive statistics
Descriptive statistics mainly studies the central tendency and Variation of data
Central trend
function | effect |
|---|---|
mean() | Calculate average |
median() | Calculate median |
mode() | Calculate mode |
prctile(X,num) | What is the num% quantile of data X |
max() | Calculate maximum |
min() | Calculate minimum |
The following functions plot statistical charts:
function | effect |
|---|---|
bar() | Draw bar chart |
stem() | Draw a needle chart |
area() | Draw fill map |
boxplot() | Draw box diagram |
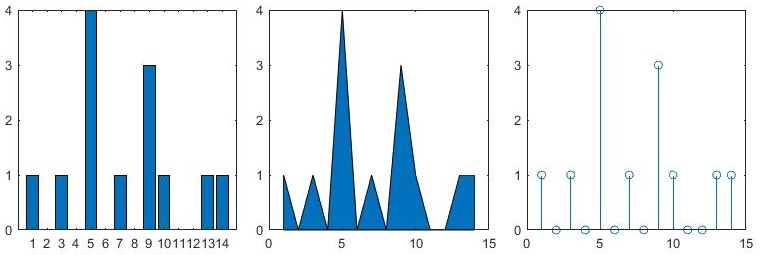
x = 1:14; freqy = [1 0 1 0 4 0 1 0 3 1 0 0 1 1]; subplot(1,3,1); bar(x,freqy); xlim([0 15]); subplot(1,3,2); area(x,freqy); xlim([0 15]); subplot(1,3,3); stem(x,freqy); xlim([0 15]);
The box chart can highlight the quartile of the data
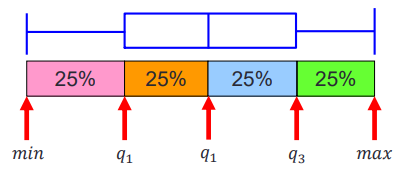
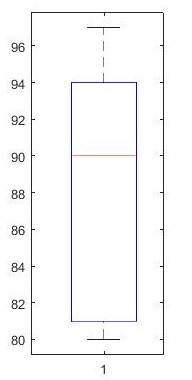
marks = [80 81 81 84 88 92 92 94 96 97]; boxplot(marks) % prctile(marks, [25 50 75]) % obtain [81 90 94]
Variation
Degree of dispersion
function | effect |
|---|---|
std() | Standard deviation of calculated data |
var() | Calculate the variance of the data |
Skewness
function | effect |
|---|---|
skewness() | Calculate the skewness of the data |
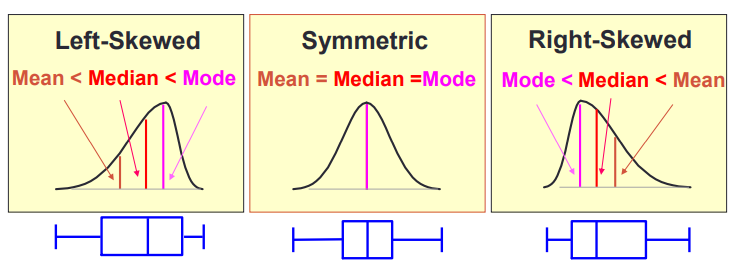
Skewness reflects the degree of symmetry of data
- When the data is biased to the left, its skewness is less than 0
- When the data is completely symmetrical, its skewness is equal to 0
- When the data is biased to the right, its skewness is greater than 0
X = randn([10 3]); % Structure 10*3 Matrix of
X(X(:,1)<0, 1) = 0; % Skew the first column of data to the right
X(X(:,3)>0, 3) = 0; % Shift the second column of data to the left
boxplot(X, {'Right-skewed', 'Symmetric', 'Left-skewed'});
skewness(X); % obtain [0.5162 -0.7539 -1.1234]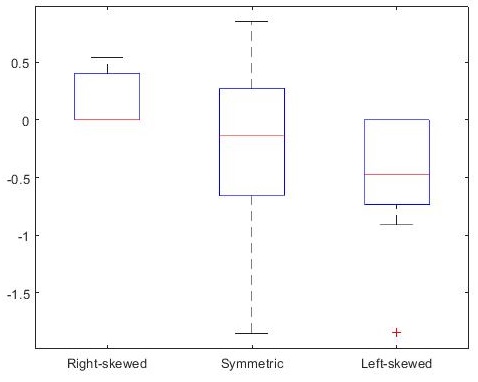
Kurtosis
function | effect |
|---|---|
kurtosis() | Calculate the kurtosis of the data |
Kurtosis represents the peak value of probability density distribution curve at the average value Intuitively, kurtosis reflects the sharpness of the peak
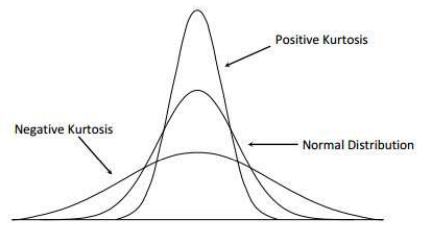
Statistical inference
The core of inferential statistics is hypothesis testing The following functions are used for hypothesis testing
function | effect |
|---|---|
ttest() | Conduct T-test |
ztest() | Perform Z-test |
ranksum() | Rank sum test |
signrank() | Sign rank test |
load examgrades x = grades(:,1); y = grades(:,2); [h,p] = ttest(x,y);
Executing the above procedure, we get [H P] = [0.9805], which means that we have no reason to refuse the same distribution of x and y under the default significance level (5%)
fitting
Polynomial fitting
Univariate polynomial fitting: polyfit()
The polyfit(x, y, n) function is used to fit the data X and Y polynomially
x = [-1.2 -0.5 0.3 0.9 1.8 2.6 3.0 3.5];
y = [-15.6 -8.5 2.2 4.5 6.6 8.2 8.9 10.0];
for i = 1:3 % Once respectively,secondary,Cubic fitting
p = polyfit(x, y, i);
xfit = x(1):0.1:x(end); yfit = polyval(p, xfit);
subplot(1, 3, i); plot(x, y, 'ro', xfit, yfit);
legend('Data points', 'Fitted curve', 'Location', 'southeast');
end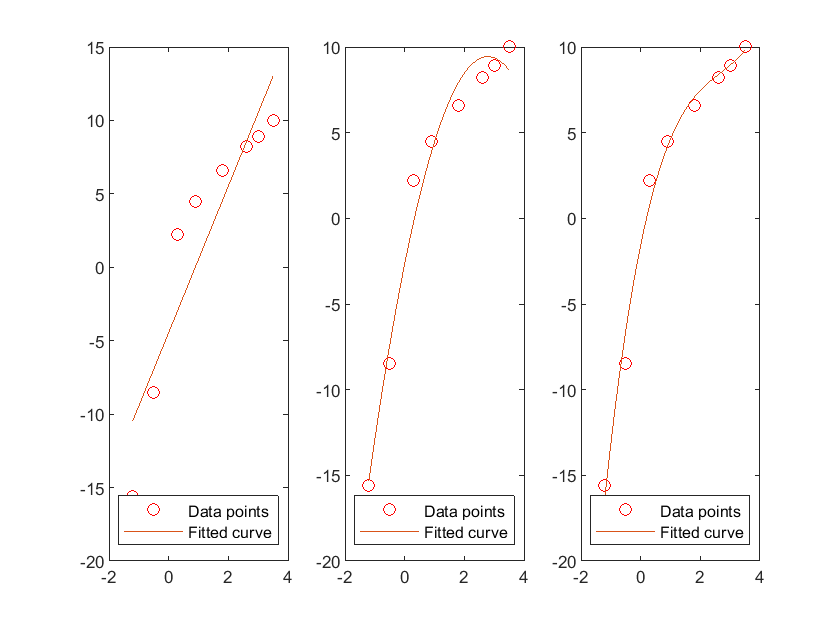
Multivariate linear fitting: regress()
Multiple linear regression is performed on data X and y using the register (y, x) function
load carsmall;
y = MPG; x1 = Weight; x2 = Horsepower; % Import dataset
X = [ones(length(x1),1) x1 x2]; % Build and expand X matrix
b = regress(y,X); % Linear regression
% The following is the drawing statement
x1fit = min(x1):100:max(x1); x2fit = min(x2):10:max(x2);
[X1FIT,X2FIT] = meshgrid(x1fit,x2fit);
YFIT = b(1)+b(2)*X1FIT+b(3)*X2FIT;
scatter3(x1,x2,y,'filled'); hold on;
mesh(X1FIT,X2FIT,YFIT); hold off;
xlabel('Weight'); ylabel('Horsepower'); zlabel('MPG'); view(50,10);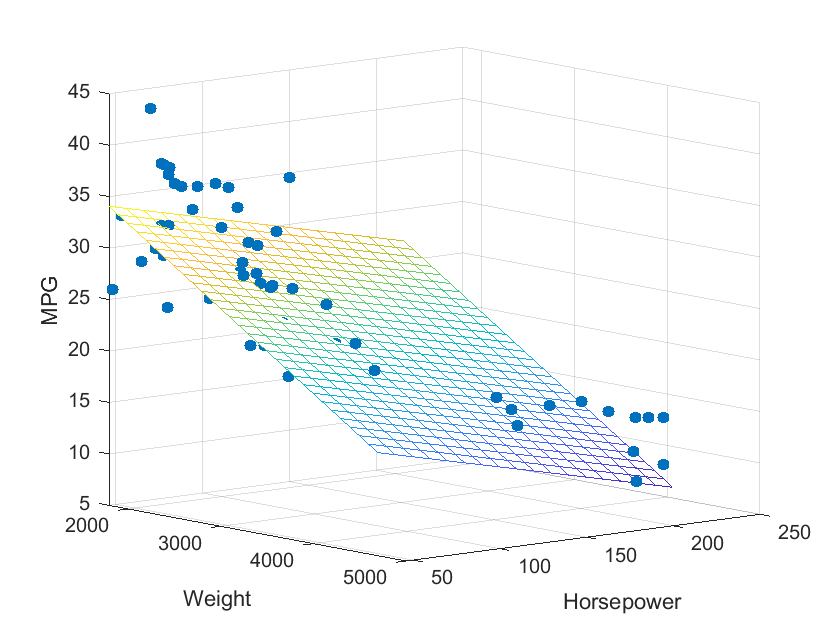
Nonlinear fitting
For nonlinear fitting, curve fitting toolbox is needed Enter cftool() in the command window to open the curve fitting toolbox
interpolation
One dimensional interpolation
function | effect |
|---|---|
interp1(x,v) or interp1(x,v,xq) | linear interpolation |
spline(x,v) or spline(x,v,xq) | Cubic spline interpolation |
pchip(x,v) or pchip(x,v,xq) | Cubic Hermite interpolation |
mkpp(breaks,coefs) | Generating piecewise polynomials |
ppval(pp,xq) | Calculate the interpolation results of piecewise polynomials |
The following examples demonstrate linear interpolation using interp1(x, v, xq) and cubic spline interpolation using spline(x, v, xq) The meaning of each parameter is as follows:
- x. V: sample points to be interpolated
- xq: query points. The function returns the interpolation results at these points
% Construction data
x = linspace(0, 2*pi, 40); x_m = x; x_m([11:13, 28:30]) = NaN;
y_m = sin(x_m);
plot(x_m, y_m, 'ro', 'MarkerFaceColor', 'r'); hold on;
% Linear interpolation of data
m_i = ~isnan(x_m);
y_i = interp1(x_m(m_i), y_m(m_i), x);
plot(x,y_i, '-b'); hold on;
% Cubic spline interpolation for data
m_i = ~isnan(x_m);
y_i = spline(x_m(m_i), y_m(m_i), x);
plot(x,y_i, '-g');
legend('Original', 'Linear', 'Spline');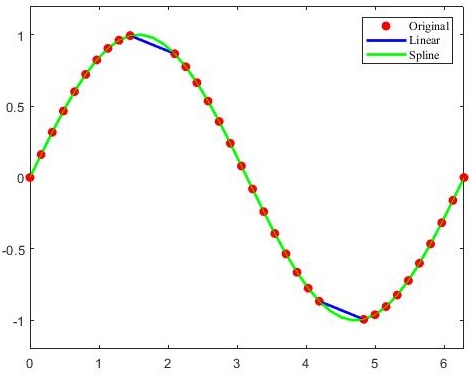
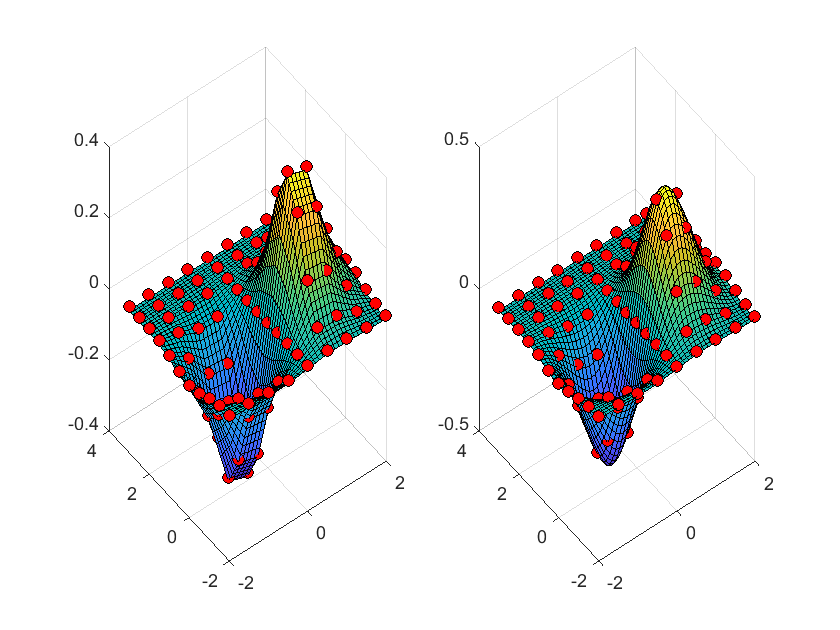
Two dimensional interpolation
interp2() can be used for two-dimensional interpolation, and the interpolation algorithm can be specified by passing a string to its method parameter
method | explain | Continuity |
|---|---|---|
'linear' | (default) the value inserted at the query point is based on the linear interpolation of the value at the grid point of the adjacent point in each dimension | C0 |
'spline' | The value inserted in the query point is based on the cubic interpolation of the value at the grid point of the adjacent point in each dimension Interpolation is based on cubic splines using non knot termination conditions | C2 |
'nearest' | The value inserted at the query point is the value closest to the sample grid point | Discontinuity |
'cubic' | The value inserted in the query point is based on the cubic interpolation of the value at the grid point of the adjacent point in each dimension Interpolation is based on cubic convolution | C1 |
'makima' | Modified Akima cubic Hermite interpolation The value inserted in the query point is based on the piecewise function of the polynomial with the largest degree of 3, which is calculated by using the values of adjacent grid points in each dimension To prevent overshoot, Akima formula has been improved | C1 |
% Build sample points xx = -2:.5:2; yy = -2:.5:3; [x,y] = meshgrid(xx,yy); xx_i = -2:.1:2; yy_i = -2:.1:3; [x_i,y_i] = meshgrid(xx_i,yy_i); z = x.*exp(-x.^2-y.^2); % linear interpolation subplot(1, 2, 1); z_i = interp2(xx,yy,z,x_i,y_i); surf(x_i,y_i,z_i); hold on; plot3(x,y,z+0.01,'ok','MarkerFaceColor','r'); hold on; % Cubic interpolation subplot(1, 2, 2); z_ic = interp2(xx,yy,z,x_i,y_i, 'spline'); surf(x_i,y_i,z_ic); hold on; plot3(x,y,z+0.01,'ok','MarkerFaceColor','r'); hold on;