I Matrix multiplication

1. Theorem:

The multiplication of two matrices can be defined only when the number of columns of the first matrix A is equal to the number of rows of the other matrix B. If a is m × N matrix and B are n × p matrices whose product C is an M × p matrix.

   

For example:

 2. thinking

1. i and j represent rows and columns respectively, so a two-dimensional matrix should be defined, and its rows and columns are 2

2. Analyze the above formula, let a*b=C, and C is the result of matrix multiplication.

(1) First line of C

The first row and the first column of C are equal to each value of the first row of a multiplied by each value of the first column of b

The first row and the second column of C are equal to each value of the first row of a multiplied by each value of the second column of b

(2) Second line of C

The first column of the second row of C is equal to each value of the second row of a multiplied by each value of the first column of b

The second row and the second column of C are equal to each value of the second row of a multiplied by each value of the second column of b

 3. code implementation

#include<stdio.h>
main()
{
	int n = 0;
	int ret1[2][3] = { {1,0,2}, {-1,3,1} };
	int ret2[3][2] = { {3,1},{2,1},{1,0} };
	int ret3[2][2];
	for (int i = 0; i < 2; i++)
	{
		
		for (int j = 0; j < 2; j++)
		{
			ret3[i][j] = 0;                 //Initialize to 0 each time
			for (int k = 0; k < 3; k++)
			{
				ret3[i][j] += ret1[i][k] * ret2[k][j];
			}
		}
	}
	for (int i = 0; i < 2; i++)             //output
	{
		for (int j = 0; j < 2; j++)
		{
			printf("%d\t", ret3[i][j]);
		}
		printf("\n");
	}
}

II Transpose matrix

1. Definition: m*n matrix

A matrix obtained by exchanging rows and columns

2. Title

Give you a two-dimensional integer array matrix and return the transpose matrix of the matrix.

Transpose of a matrix refers to flipping the main diagonal of the matrix and exchanging the row index and column index of the matrix.

< 1 > idea:

You can exchange row indexes and column indexes directly

< 2 > code

#include<stdio.h>
main()
{
	
	int ret[3][3] = { {2,4,-1},{-10,5,11},{18,-7,6} };//Define a two-dimensional matrix
	int newret[3][3];                                //Define a new matrix
	for (int i = 0; i < 3; i++)                      //Traverse rows and columns respectively
	{
		for (int j = 0; j < 3; j++)
		{
			newret[i][j] = ret[j][i];               //Column index row index exchange
			printf("%d\t", newret[i][j]);
		}
		printf("\n");
	}



}

< 3 > results

III Matrix rotation

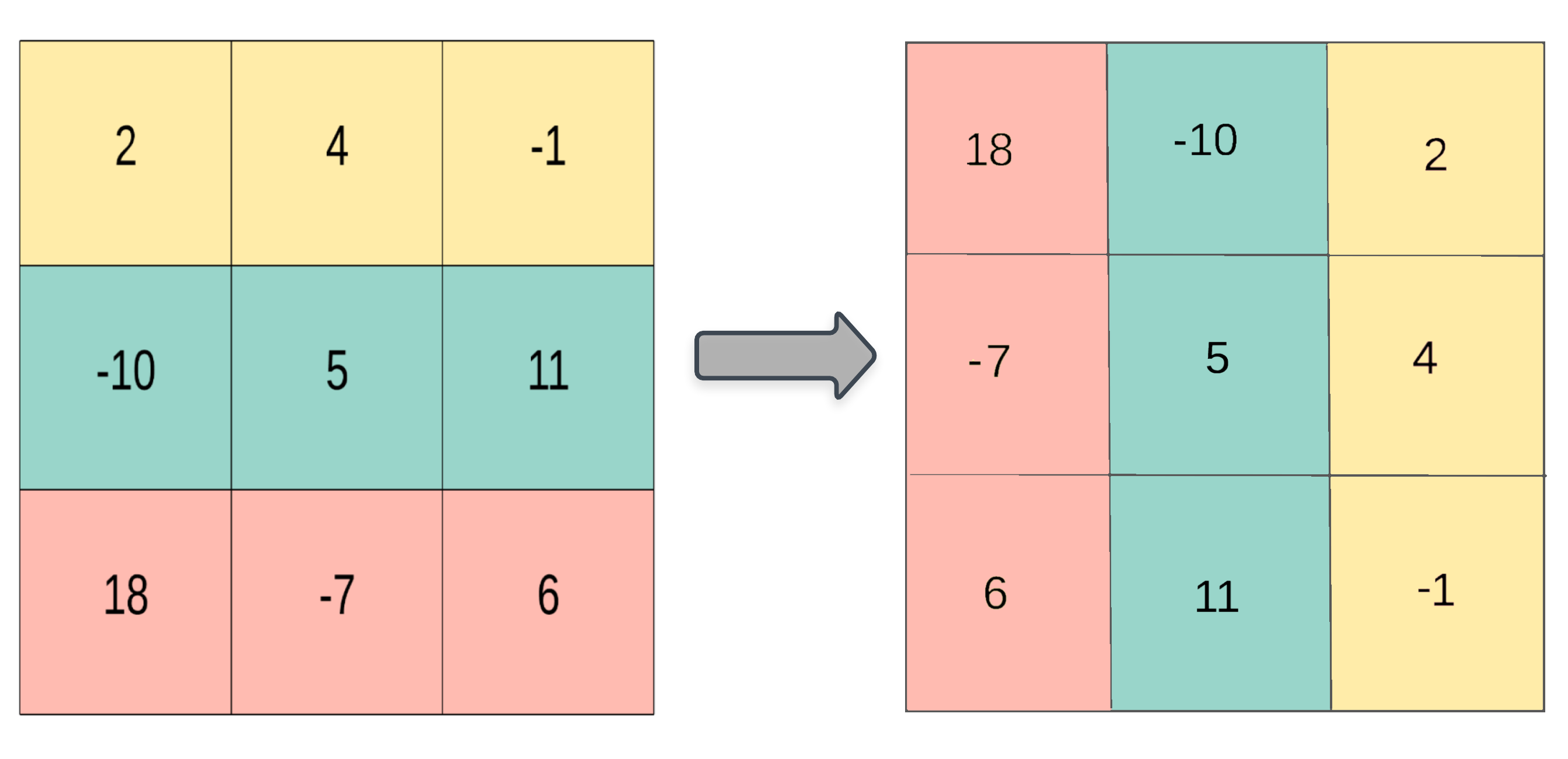
Rotate 90 ° clockwise

1. Ideas

Change of coordinates of 4: (0, 1) - > (1,1)

Other numbers are the same, so we don't list them one by one

For the ＾ j element in the ＾ i ＾ row of the matrix, it appears at the ＾ j ＾ position in the penultimate ＾ i ＾ column after rotation.

Translate into code

For matrix elements, matrix[i][j] becomes matrix2[j][n-i-1] after rotation; In the following code, n is 3,

2. Code

<1> According to the above rules, rotate the matrix and put the elements of the matrix into matrix2.

<2> Output rotated matrix

{
	int matrix[3][3] = { 2,4,-1,-10,5,11,18,-7,6 };
	int matrix2[3][3];
	
	for (int i = 0; i < 3; i++)
	{
		for (int j = 0; j < 3; j++)
		{
			matrix2[j][3-i-1] = matrix[i][j];      //Rotate the matrix according to the rules
		}

	}

	for (int i = 0; i < 3; i++)
	{
		for (int j = 0; j < 3; j++)
		{
			printf("%d\t", matrix2[i][j]);         //Output rotated matrix
		}
		printf("\n");
	}
}

 

Rotate 90 ° counterclockwise (equivalent to 270 ° counterclockwise)

1. Ideas

4:(0，1)--->(1,0)

Other numbers are the same, so we don't list them one by one

For the ＾ j element in the ＾ i ＾ row of the matrix, it appears at the ＾ j ＾ position in the penultimate ＾ i ＾ column after rotation.

Translate into code

For matrix elements, matrix[j][n-i-1] becomes matrix2[i][j] after rotation; In the following code, n is 3,

2. Code

<1> According to the above rules, rotate the matrix and put the elements of the matrix into matrix2.

<2> Output rotated matrix

{
	int matrix[3][3] = { 2,4,-1,-10,5,11,18,-7,6 };
	int matrix2[3][3];
	
	for (int i = 0; i < 3; i++)
	{
		for (int j = 0; j < 3; j++)
		{
			matrix2[i][j] = matrix[j][3-1-i];           //The difference with clockwise rotation
		}

	}

	for (int i = 0; i < 3; i++)
	{
		for (int j = 0; j < 3; j++)
		{
			printf("%d\t", matrix2[i][j]);
		}
		printf("\n");
	}


}

 

180 ° clockwise (equivalent to 180 ° counterclockwise)

 

1. Ideas

4:(0，1)--->(2,1)

Other numbers are the same, so we don't list them one by one

For the ＾ j element in the ＾ i ＾ row of the matrix, it appears at the ＾ j ＾ position in the penultimate ＾ i ＾ column after rotation.

Translate into code

For the elements of the matrix, matrix[i][j] becomes matrix2[n-j-1][n-i-1] after rotation; In the following code, n is 3,

2. Code

<1> According to the above rules, rotate the matrix and put the elements of the matrix into matrix2.

<2> Output rotated matrix

main()
{
	int matrix[3][3] = { 2,4,-1,-10,5,11,18,-7,6 };
	int matrix2[3][3];
	
	for (int i = 0; i < 3; i++)
	{
		for (int j = 0; j < 3; j++)
		{
			matrix2[3 - i - 1][3 - j - 1] = matrix[i][j];
		}

	}

	for (int i = 0; i < 3; i++)
	{
		for (int j = 0; j < 3; j++)
		{
			printf("%d\t", matrix2[i][j]);
		}
		printf("\n");
	}


}

3. The results are as follows