I'll go. I feel amazing after reading this divide and rule, but I don't understand it very well. So when learning this place, I should have a good taste and check the information on the Internet. Here's my understanding:

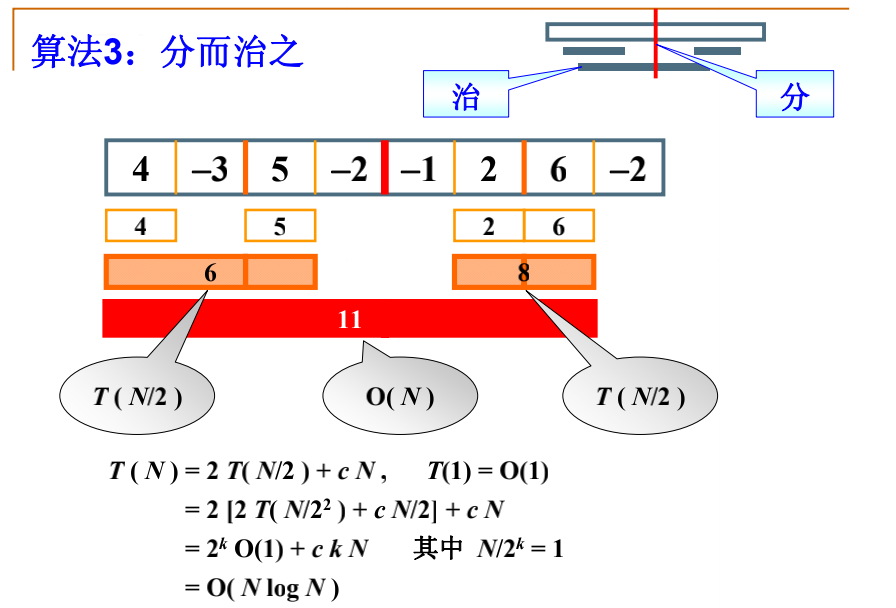
The eight numbers are separated in the middle, the left ones are separated in turn, and the right ones are separated in turn:

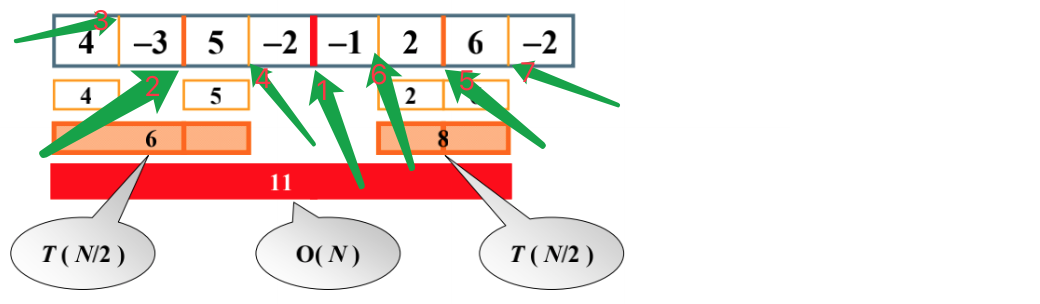
That is to divide the whole into half, continue to divide half on the left, continue to divide half, continue to divide half on the right, and then continue to divide half.
After scoring:
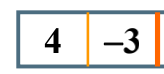The largest child column sum on the left of is 4, and the right is a negative number, so a 0 is returned;
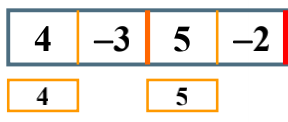
The largest child column sum on the left of is 5, and the right is a negative number, so a 0 is returned;
So there is such a result.
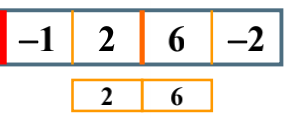
The left side of the column is a negative number, so a 0 is returned, and the maximum sum of the child columns on the right is 2
The largest child column sum on the left of is 6, and the right is a negative number, so a 0 is returned;
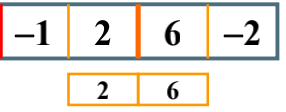So there is such a result.



Because the maximum sum of the left and right sub columns in the middle is found, but there is also a maximum sum of the sub columns across the boundary. After finding the maximum sum of the sub columns across the boundary, the largest of the three is the result we want.
How to find the maximum sum of sub columns across the boundary? Start scanning to the left in the middle, - 3,1 (- 3 + 4), so the left is 1 and the right is 5,3 (5-3), so the maximum sum of sub columns across the boundary is 1 + 5 = 6 > 5 > 4, so the result here is 6.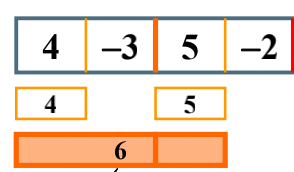


Similarly:
The maximum sum of sub columns across the boundary is 8 > 6 > 2, so the result we get here is 8.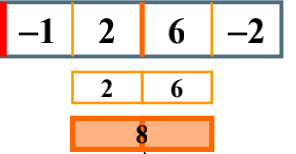


Similarly: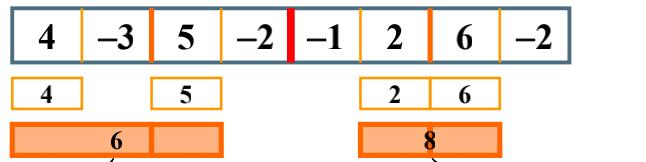The maximum sum of sub columns across the boundary is 4 + 7 = 11 > 6 > 8, so the final result is 11
4=(-2+5-3+4)
7=(-1+2+6)

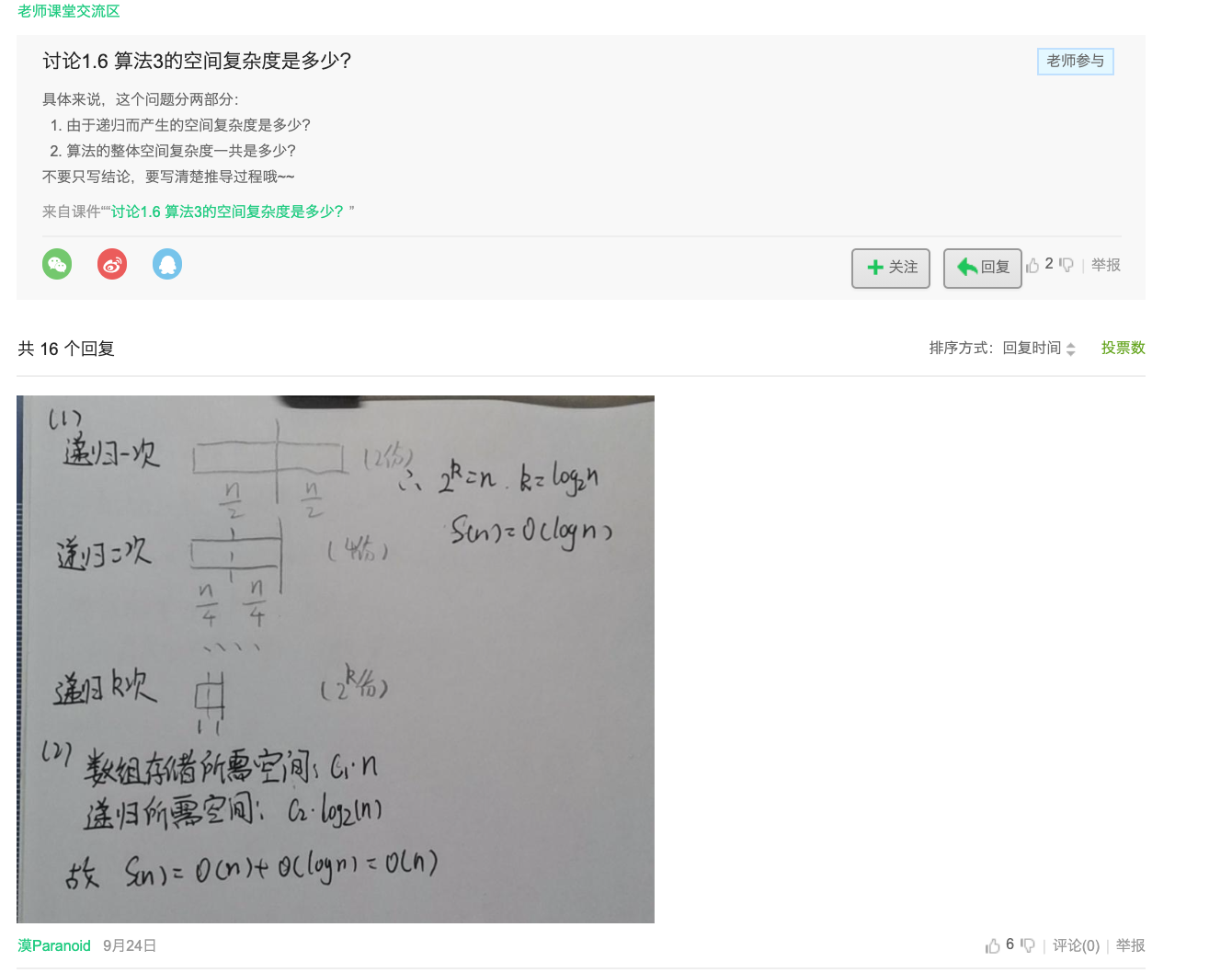
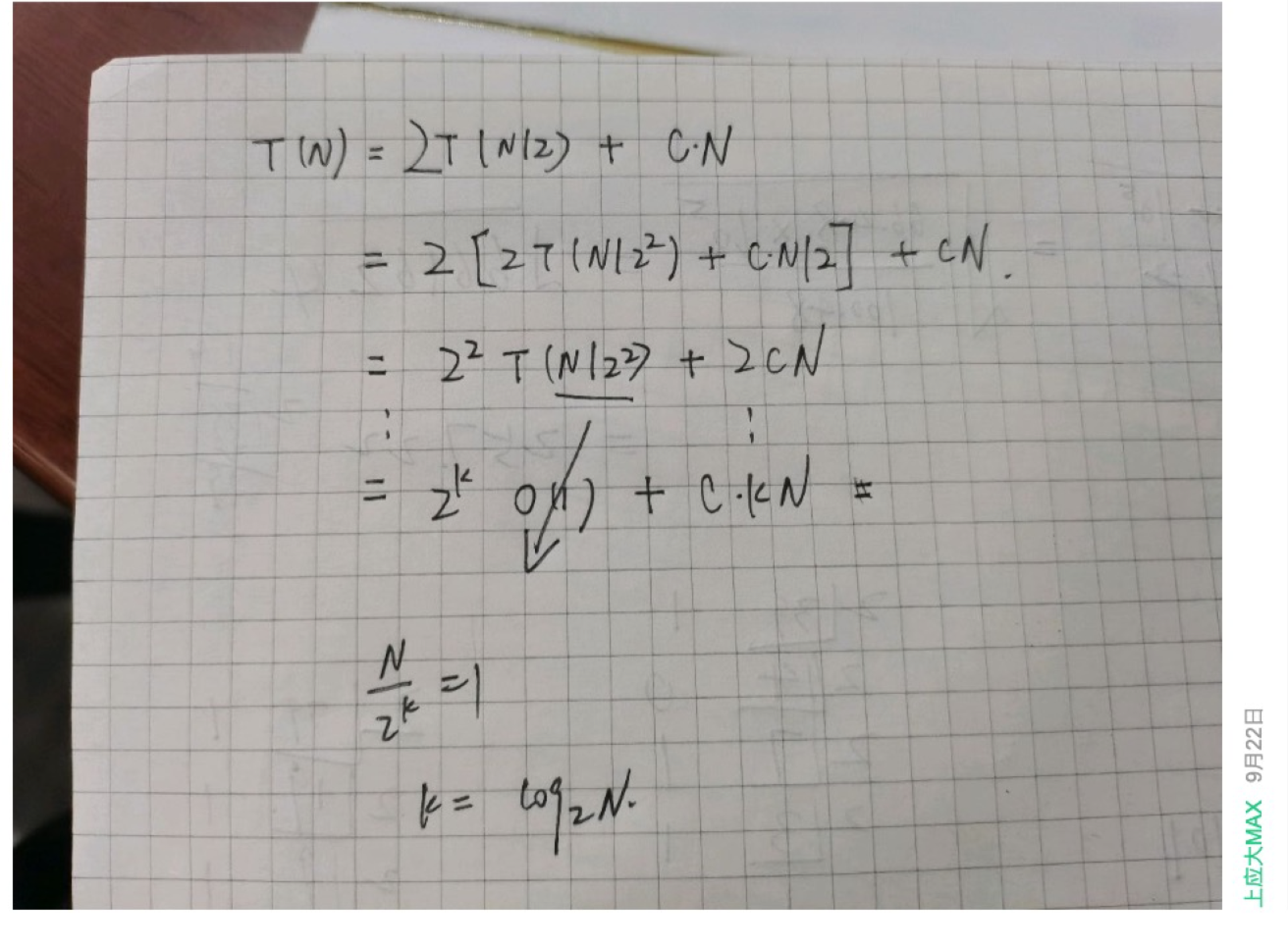
Obviously, there is only one for loop in these codes. All if else in the for loop are of constant order of magnitude complexity, so the complexity of this algorithm is O(n), which is linear.


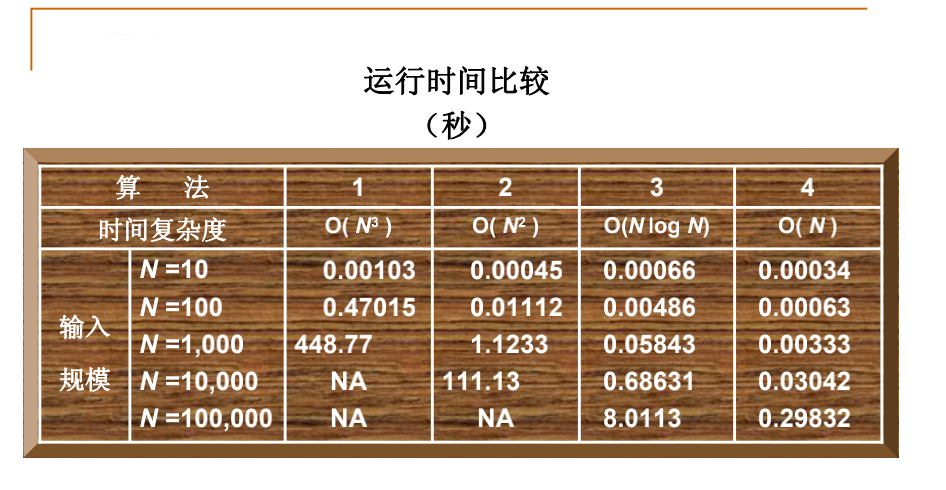
This efficiency is higher than the first three algorithms. The high efficiency of the algorithm has side effects. The side effect is that its correctness is not very obvious. In other words, it's a little difficult for others to understand how the program works

Explain:

First, add the first number - 1, and then find that this number is less than 0, so the current sub column sum is negative, so discard it directly (because the maximum sub column sum must start from a positive number, and a negative number is equivalent to a negative number at the beginning, so the first negative number must not constitute the maximum sub column sum, so discard the first negative number directly.)

Then add the second number 3 to the sub column sum, greater than 0, and update this value to the maximum sub column sum.

At this time, after adding - 2 to the sub column sum, the value of the sub column sum is 1, greater than 0, but ThisSum is smaller than MaxSum, so the if statement is not executed, that is, the maximum sub column and MaxSum will not change, and ThisSum will not be abandoned, because it is still a positive number, and the following sum may always become larger.

At this time, add 4, and then the maximum sub column sum becomes 5. Update the maximum sub column sum

At this time, if you add - 6 and the whole becomes a negative number, you will discard all these, but the maximum child column and are not discarded at this time

Adding 1 doesn't change much, and then adding 6 becomes 7, which is larger than the original maximum sub column sum, so the maximum sub column sum is updated

int Max3( int A, int B, int C )
{ /* Returns the maximum of 3 integers */
    return A > B ? A > C ? A : C : B > C ? B : C;
}

int DivideAndConquer( int List[], int left, int right )
{ /* Divide and conquer to find the maximum sum of sub columns from List[left] to List[right] */
    int MaxLeftSum, MaxRightSum; /* Solution of left and right subproblems */
    int MaxLeftBorderSum, MaxRightBorderSum; /*Store results across boundaries*/

    int LeftBorderSum, RightBorderSum;
    int center, i;

    if( left == right )  { /* The termination condition of recursion. The sub column has only 1 number */
        if( List[left] > 0 )  return List[left];
        else return 0;
    }

    /* The following is the process of "dividing" */
    center = ( left + right ) / 2; /* Find the midpoint */
    /* Recursively find the maximum sum of two sub columns */
    MaxLeftSum = DivideAndConquer( List, left, center );
    MaxRightSum = DivideAndConquer( List, center+1, right );

    /* Next, find the maximum sum of sub columns across the boundary */
    MaxLeftBorderSum = 0; LeftBorderSum = 0;
    for( i=center; i>=left; i-- ) { /* Scan left from midline */
        LeftBorderSum += List[i];
        if( LeftBorderSum > MaxLeftBorderSum )
            MaxLeftBorderSum = LeftBorderSum;
    } /* Left scan end */

    MaxRightBorderSum = 0; RightBorderSum = 0;
    for( i=center+1; i<=right; i++ ) { /* Scan right from midline */
        RightBorderSum += List[i];
        if( RightBorderSum > MaxRightBorderSum )
            MaxRightBorderSum = RightBorderSum;
    } /* Right scan end */

    /* The result of "governance" is returned below */
    return Max3( MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum );
}

int MaxSubseqSum3( int List[], int N )
{ /* Maintain the same function interface as the first two algorithms */
    return DivideAndConquer( List, 0, N-1 );
}