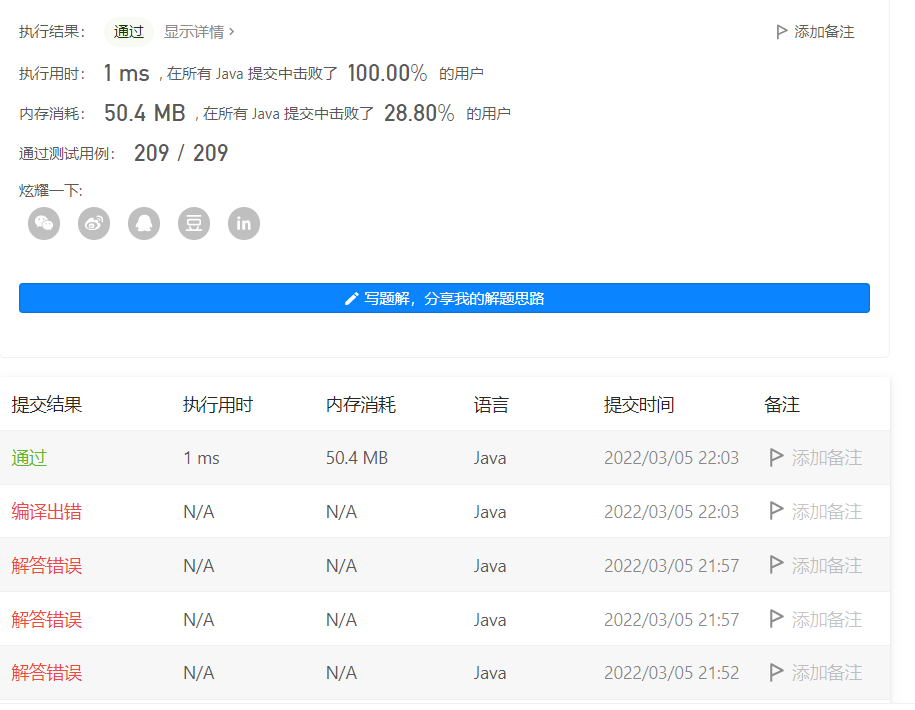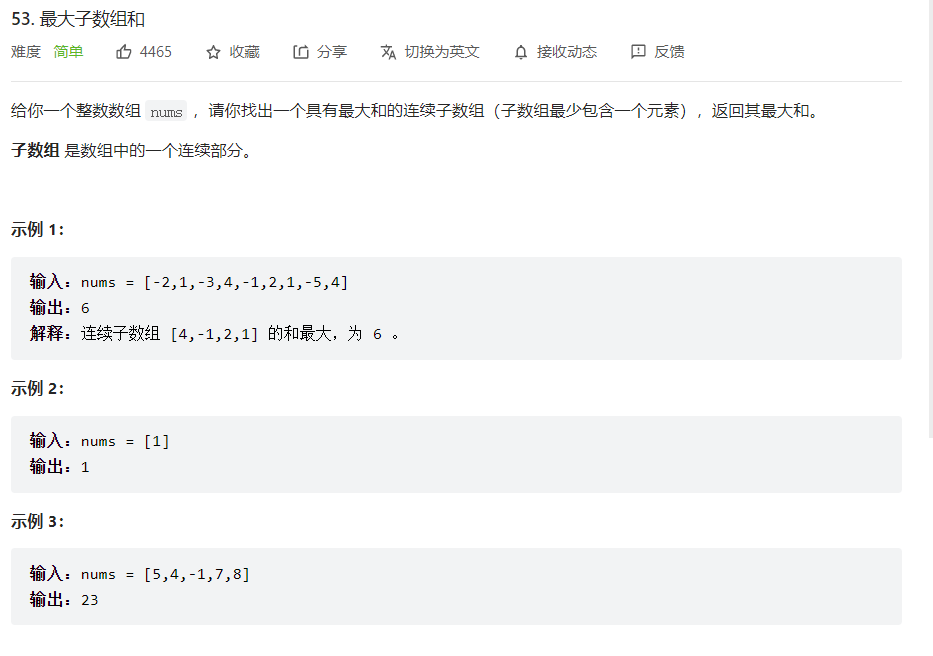
Note that you are looking for a continuous array!!

1, Dynamic programming method

 class Solution {
    public int maxSubArray(int[] nums) {
        //Create an array dp as large as nums
       int[] dp=new int[nums.length];
        //dp[i] represents the sum of the largest subarray of the array ending in num [i]
       dp[0]=nums[0];
       for(int i=1;i<nums.length;i++){
       // If DP [I-1] + num [i] > = num [i], the largest subarray of num [i] is the largest subarray of num [I-1] plus num [i]; If DP [I-1] + num [i] is smaller than num [i], the largest subarray of num [i] is itself
           if(dp[i-1]+nums[i]>=nums[i]){
               dp[i]=dp[i-1]+nums[i];
           }else{
               dp[i]=nums[i];
           }
       }
      //The largest subarray of the whole num array is the maximum value of the largest subarray of the array ending with each element in the num array
        //So go through the dp array again to find the maximum value
       return max(dp);
    }
    public int max(int[] dp){
        int max=dp[0];
        for(int i=0;i<dp.length;i++){
             if(dp[i]>=max){
                 max=dp[i];
             }
        }
        return max;
    }

1. Determine the sub problem

For example, the num given by the title = [5,4, - 1,7,8]

We can decompose this problem into:

What is the sum of the largest consecutive subarrays ending in 5?

What is the sum of the largest consecutive subarrays ending in 4?

What is the sum of the largest consecutive subarrays ending in - 1?

What is the sum of the largest consecutive subarrays ending in 7?

What is the sum of the largest consecutive subarrays ending in 8?

2. Find the relationship and establish the dynamic transfer equation

It can be found that the continuous array ending in 4 is the continuous array ending in 5 plus 4. If the sum of the continuous largest subarray ending in 5 plus 4 is greater than 4, then the largest subarray ending in 4 is the number of continuous largest subarrays ending in 5 plus 4; Otherwise, it is 4 itself

Then let's create a dp array as large as nums. dp[i] represents the sum of the continuous largest sub arrays ending in nums[i]

dp[i]={   dp[i−1]+nums[i]，     if             dp[i]>0  (dp[i−1]+nums[i]>num[i])

             nums[i],​                   if            dp[i−1]≤0​          }

The largest subarray of the whole num array is the maximum value of the largest subarray of the array ending with each element in the num array
So go through the dp array again to find the maximum value

2, Greedy algorithm

The whole traversal from the front to the back is through the array, and Max is used to represent the current largest sub array and, constantly update max, and finally return max. Sum is used to represent the largest array on num [i] plus num [i], Max takes the maximum value in Max and sum (constantly updating max). If sum < 0, Num [i] cannot be added, and the continuous array will be directly broken and searched again from num [i + 1]. Because num [i + 1] plus sum is equivalent to adding a negative number, it's better not to add it, so sum is directly changed to 0

Finally, return to max

But we ignore a situation: all negative numbers, so sum can't be positive, but it returns 0

So you can judge this situation at the front and return the largest negative number in the array

class Solution {
    public int maxSubArray(int[] nums) {
       int sum=0;
       int max=Integer.MIN_VALUE;
       if(nums.length==1){
           //If the array has only one element, this element is returned directly
           return nums[0];
       }
             //Determine whether all numbers are negative
    for(int i=0;i<nums.length;i++){
        if(nums[i]>=0){
            // If one is not negative, it will jump out
            break;
        }
        if(i==nums.length-1&&nums[nums.length-1]<0){
            //If you can traverse to the last element and the last element is negative, you will return the maximum number in the array
            max=max(nums);
            return max;
        }
    }
       for(int i=0;i<nums.length;i++){
           if(sum+nums[i]<0){
                   //If num [i] is small enough to cancel sum, the continuous array will be broken and the next one will be found
                    sum=0;
           }else{
               sum=sum+nums[i];
               //Constantly update max
               max=Math.max(sum,max);
           }
       }
       return max;
    }
    public int max(int[] nums){
        int max=nums[0];
        for(int i=1;i<nums.length;i++){
            if(nums[i]>max){
                max=nums[i];
            }
        }
        return max;
    }
}