introduction
I'm trying to write a blog for the first time. I hope you officials will be more tolerant
If there are mistakes, I hope you can put them forward. I will correct them in time. Thank you
At his best age, he found his future goal
There is still one year to struggle and brush questions. Go to interview and practice next year. Come on!
Today, I will share some ideas with you
Topic 5 requirements:
This topic and Luogu P1006 Consistent, interested students can also Kangkang
Overall idea 1: (violence) DP
A passes the note to B. in the process of B passing it back, if we look backwards, it is equivalent to a passing two notes at the same time. Because if we consider DP in both directions at the same time, the complexity must be very large. It is very difficult to judge whether they have visited a node. So we might as well look at the opposite. From B to a is the reverse process of a to B. in this way, the two roads are carried out at the same time, but when we reach a point at the same time, we can only keep the favor of one point, because only one road can access here.
1. Steady state
We start from (1,1) at the same time. They go to (i,j)(k,l) respectively, so we must indicate where they have gone, so there are four states of violence. The first two indicate where the first road has gone, and the last two indicate where the other road has gone.
2. Initialize
Because there is no favorability value at the beginning, it is 0
3. Find transfer
Remember: when looking for the transfer, we should grasp that "the large interval is transferred through the small interval, plus its own consumption". When this topic comes to (i,j)(k,l), the natural consumption is a[i][j]+a[k][l], which is fixed, so the search for the optimal depends on the sub interval. The sub interval is optimal, and the interval is optimal. This is a typical interval DP. The state transfer template is as follows:
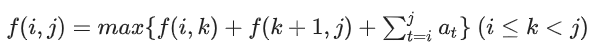
Back to this question, because dp[i][j][k][h] has four sub States, and each point can only be in two directions, right and down, so 2 * 2 = 4 sub States, which can be written directly here without enumeration.
1. When node 1 reaches this node to the right, node 2 may be dp[i - 1][j][k - 1][h] dp[i - 1][j][k][h - 1].
2. When node 1 goes down to this node, node 2 may be dp[i][j - 1][k - 1][h] dp[i][j - 1][k][h - 1].
Therefore, it is OK to find the optimal solution in these four sub States, plus this consumption, so the maximum value is taken.
4. Find the answer
When both points reach the end point, i.e. dp[m][n][m][n]
Specific code
Note that the question says that each node can only be accessed once, so once the current points of the two paths conflict, only one favorable degree will be left
#include <iostream>
#include <algorithm>
using namespace std;
//Violent DP
int dp[51][51][51][51] = { };
int a[51][51];//matrix
int m, n;//Row, column
int main()
{
cin >> m >> n;
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
scanf("%d", &a[i][j]);
}
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
for (int k = 1; k <= m; k++) {
for (int h = 1; h <= n; h++) {
dp[i][j][k][h] = max(max(dp[i - 1][j][k - 1][h], dp[i - 1][j][k][h - 1]), max(dp[i][j - 1][k - 1][h], dp[i][j - 1][k][h - 1])) + a[i][j] + a[k][h];
//Select the best (i.e. maximum) + this consumption from the four sub states
//If the consumption of this interval is related to the selection of sub interval, this consumption will be
//Put it into the sub interval selection to ensure the optimal result
if (i == k && j == h) {//You can only walk once at the same point
dp[i][j][k][h] -= a[k][h];//If the visit conflicts, the goodwill will only be increased once
}
}
}
}
}
cout << dp[m][n][m][n];//The result is when both points reach the end
}
(all codes have been run correctly)
After testing, the running condition of the code is (the shortest time after multiple tests):

This idea is very direct and simple, but the time complexity is at least O(n^4), and it also consumes a lot of space. A lot of redundant calculations are done. Once the card data is finished.
Overall idea 2: 3D DP
In our previous method, first, we did a lot of redundant calculations. When the first path is selected (i,j), it is impossible to select the second path again (i,j). Then, we only need to select the remaining selectable points to reduce the complexity; Second: the dimension is too large, the number of cycle layers is too many, and the batch with high space-time complexity, so it is necessary to reduce the dimension to reduce the space-time complexity.
1. Steady state
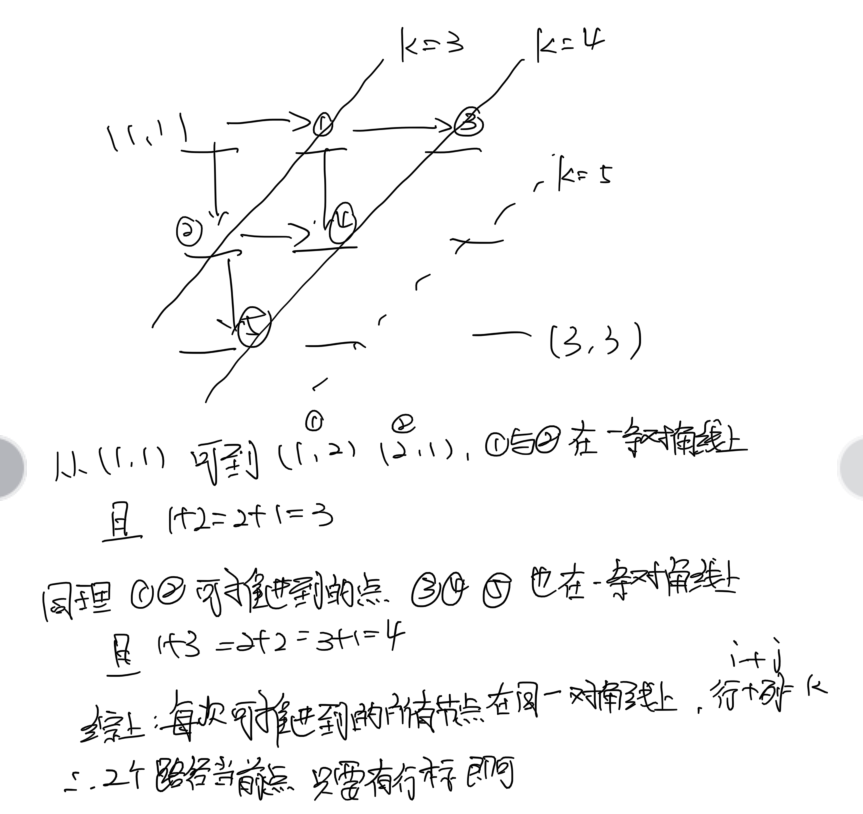
First of all, our goal is to reduce the dimension. The larger the dimension, the greater the space-time complexity. As can be seen from the above figure, starting from the source point, the point that can be pushed each time must be on a diagonal, and k=i+j is fixed. Therefore, I only need to know the row where the two path endpoints are located, so I can deduce the column number through k, so there are three states: k, I and J.
2. Initialize
Because there is no favorability value at the beginning, it is 0
3. Find transfer
Remember: when looking for the transfer, we should grasp that "the large interval is transferred through the small interval, plus its own consumption". When this topic comes to (i,k-i)(j,k-j), the natural consumption is a[i][k - i] + a[j][k - j], which is fixed. Therefore, the search for the optimization depends on the sub interval. The sub interval is the best, and the interval is the best. This is a typical interval DP. The state transition template is as follows:
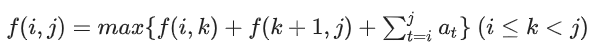
When we go to dp[k][i][j], what is his sub interval? That is, many states of k-1 in the last promotion. We can find the optimal solution through many states last time. In addition, our consumption this time is the optimal solution this time. Note that I and j are rows. When we look at the sub state of the last promotion, we look at the relationship between the two rows (rows can only be downward)
Substatus 1:
dp[k - 1][i][j]: the relationship between two rows remains unchanged
Substatus 2:
dp[k - 1][i - 1][j]: the line of the first path drops to i, and j remains unchanged
Substatus 3:
dp[k - 1][i][j - 1]: the line of the second path drops to j, and I remains unchanged
Substatus 4:
dp[k - 1][i - 1][j - 1]: the line of the first path drops to i, and the line of the second path drops to j
To sum up: find the optimal + self consumption in the four sub states
4. Find the answer
When k=m+n-1, it's almost a push to the meeting point. The meeting point has no favor, so the penultimate step is the answer, namely dp[m + n - 1][m - 1][m];
Specific code
Note:
1. In order to reduce redundant calculation, the selected nodes should not be repeated. Therefore, in the implementation, line I occupies the corresponding point (i,k-i) of this promotion, and this point should not be selected for the other path, because it has been helped once, and the other path needs to enumerate the available points backward, so j=i+1 is used as the initial path
2. Look at the diagram drawn above to find the state. When k=3, the maximum number of columns that can be pushed is k-i=1, so it is necessary to cross the boundary.
#include <iostream>
#include <algorithm>
using namespace std;
//3D DP
int dp[200][200][200] = {};
int a[51][51];
int m, n;
int main()
{
cin >> m >> n;
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
scanf("%d", &a[i][j]);
}
}
for (int k = 3; k < m + n; k++) {//k starts from 3 to m+n-1. I don't understand. Look at the figure above me
for (int i = 1; i <= m; i++) {//The lines of the first path are possible from beginning to end
for (int j = i + 1; j <= m; j++) {//In order to reduce redundant calculation, i go through line i, so i go from j=i+1
//In this way, the reader will have a question that when i=1, j cannot appear on line 1, but when i=2, j can appear on line 1,
//But let's put it another way, isn't this repeated when i=1, because I and j are just two arbitrary lines, No
//But for the sake of intuitive code, i is above j by default. In fact, there is no strict position difference between the two
//So you can't ask one person to help you twice at the same time, so j takes it after i
if (k - i < 1 || k - j < 1) {//Use the column to determine the out of bounds
continue;
}
dp[k][i][j] = max(max(dp[k - 1][i][j], dp[k - 1][i - 1][j]), max(dp[k - 1][i][j - 1], dp[k - 1][i - 1][j - 1])) + a[i][k - i] + a[j][k - j];
//Select the best (i.e. maximum) + this consumption from the four sub states
//If the consumption of this interval is related to the selection of sub interval, this consumption will be
//Put it into the sub interval selection to ensure the optimal result
}
}
}
cout << dp[m + n - 1][m - 1][m];
}
(all codes have been run correctly)
After testing, the running condition of the code is (the shortest time after multiple tests):

 (by comparing this time with the above one, we can see that it has been reduced by one dimension, which can greatly reduce the time complexity)
(by comparing this time with the above one, we can see that it has been reduced by one dimension, which can greatly reduce the time complexity)
If the time complexity is O(n^3) when it is reduced to three dimensions, the complexity can be greatly reduced. Then we can reduce the dimension to two dimensions again by scrolling the array, which will be faster. However, bloggers are not very good at scrolling the array for the time being, so I b learned to update it later.
Topic 4 requirements

Overall thinking
This question is equivalent to asking. Set a time for you to arrange as many people to work as possible. We must choose who works fast, choose who first, and finish what works fast according to common sense. Then I can arrange more people. This is the idea of this question.
code
Note: because you want to sort the structure, which is a user-defined data structure and is not bui lt-in, you need to tell me how to arrange the sort function, so overload the < operator, tell me how to sort and what logic to follow internally. At this time, < is just a symbol, and sort will automatically call the overload operator function.
#include <iostream>
#include <algorithm>
using namespace std;
struct mission {
int stime;
int etime;
int idx;
bool operator < (const mission & node) const {//Overloaded operator<
return etime < node.etime;//Guarantee from small to large deadline
}
};
mission a[1000];
int answer = 1;
int n;
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i].stime >> a[i].etime;
}
sort(a + 1, a + 1 + n);//Sort the deadline from small to large. See overloaded operator functions for specific comparison methods
int pre = a[1].etime;//The fastest one must be selected as the precursor to dynamically find the number
for (int i = 2; i <= n; i++) {
int temp = a[i].stime;
if (temp > pre) {//If the start time is greater than the precursor deadline, choose
answer++;//to update
pre = a[i].etime;
}
else {
continue;
}
}
cout << answer;
}
(all codes have been run correctly)
After testing, the running condition of the code is (the shortest time after multiple tests):

Topic 3 requirements
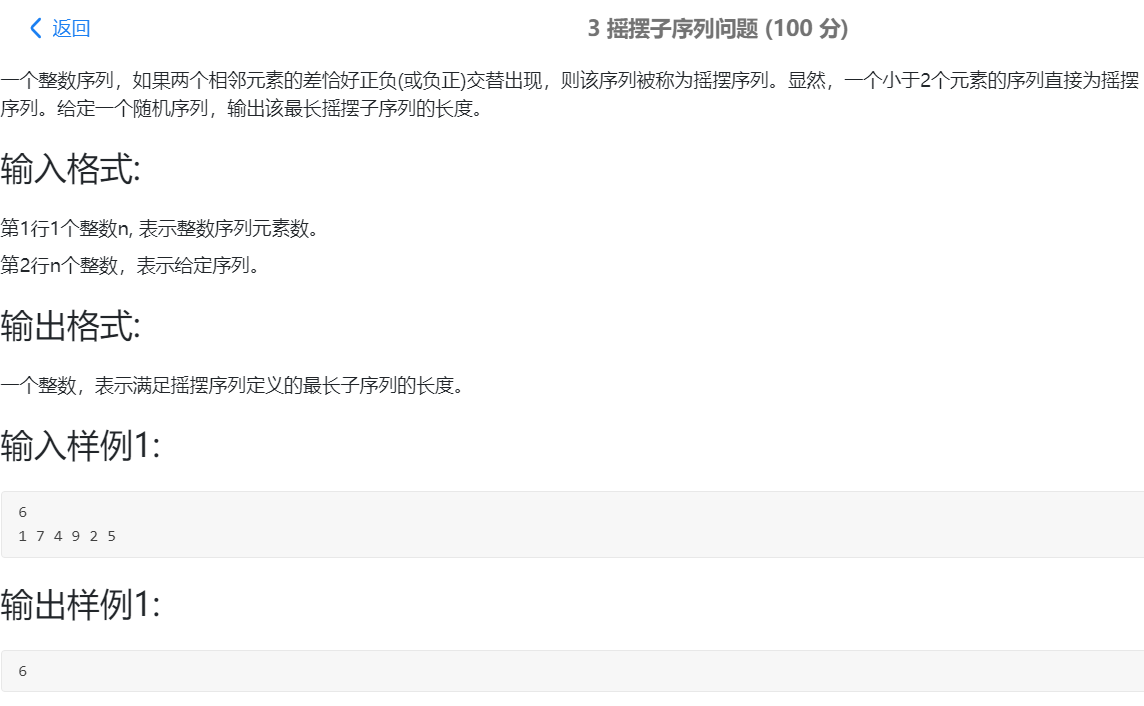
Overall thinking
Let's scan this array dynamically. We can update it while scanning and judging.
code
Note: it is "front rear"!!!
#include <iostream>
#include <algorithm>
using namespace std;
int n;
int a[10000];//Store target data
int ans = 0;
int main() {
cin >> n;
if (n <= 2) {
cout << n;
return 0;
}
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
int pre = a[1] - a[2];//precursor
int temp_ans = 1;//Temporary number, used to record the number of a certain section, and finally take the maximum value with the answer
//Because you want the maximum length
for (int i = 2; i <= n; i++) {
int temp = a[i] - a[i + 1];
if (i == n) {//The last cycle is used to update the ans record, otherwise it will be updated less than once
//Quit after the penultimate update. I didn't have time to update ans
ans = max(ans, temp_ans);
}
if (temp*pre < 0) {//It's a swing queue
pre = temp;//to update
temp_ans++;
}
else {
ans = max(ans, temp_ans);//If not, update ans
temp_ans = 1;//These need to be updated because they need to continue to find
pre = temp;
}
}
cout << ans+1;//The final answer is always one less, so + 1 output
}
(all codes have been run correctly)
After testing, the running condition of the code is (the shortest time after multiple tests):

Topic 2 requirements
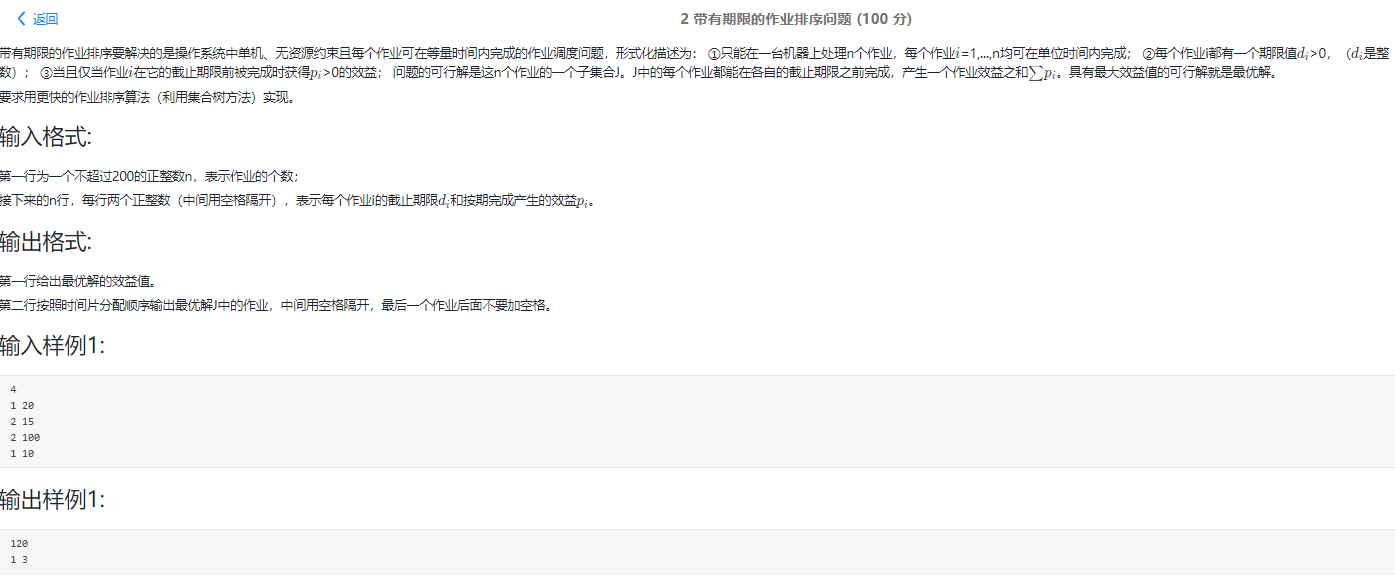
Overall thinking
The idea is very simple. I'm greedy for the maximum benefit, so I let it appear at the position of his deadline every time. If the deadline is too large and exceeds n, the default deadline is n. if the position of the deadline is occupied, we need to look up the position where his precursor can be inserted through and search.
code
Note: in order to search forward quickly, the idea of set tree (and search set) is introduced.
#include <iostream>
#include <algorithm>
using namespace std;
struct mission {
int time;//deadline
int value;//value
int idx;//Serial number
bool operator < (const mission & node) const {
return value > node.value;//This is the sorting of structures to ensure from large to small
}
};
bool isVisit[1000] = { false };//Judge whether to walk here
mission a[1000];
int answer[1000];//answer
int ano[1000] = { 0 };//Joint search set
int n;
int val = 0;//Total value
int num = 0;//Record the total number that can be put in
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i].time;
if (a[i].time > n) {
a[i].time = n;
}
cin >> a[i].value;//initialization
a[i].idx = i;
ano[i] = i;
}
sort(a + 1, a + 1 + n);
for (int i = 1; i <= n; i++) {
bool flag = false;
int item = a[i].time;//Check deadline 1
int size = ano[item];//Find the possible place of the deadline in the answer sequence in the parallel search set
if (size == 0) {//If it is zero, it means it cannot be put in
continue;
}
if (!isVisit[size]) {//You can put it in the corresponding position
answer[size] = a[i].idx;
val += a[i].value;
num = size;
ano[size] = ano[size - 1];//Query set update operation
isVisit[size] = true;
}
else {
while (1) {//I can't fit the position I found, so
size = ano[size];//Loop through the search set to find the points that can be put in
if (size == 0) {//0 means you can't put it in
flag = true;
break;
}
if (!isVisit[size]) {
break;
}
}
if (flag) {//flag is true, which means it can't be put in
continue;
}
else {
answer[size] = a[i].idx;//Put it in the same way as above
val += a[i].value;
num = size;
ano[size] = ano[size - 1];
isVisit[size] = true;
}
}
}
printf("%d\n", val);
int i = 1;
for (; i < num; i++) {//Output (there may be a small error here. You can ignore here. The topic is still the joint search set)
if (answer[i] != 0) {
printf("%d ", answer[i]);
}
}
printf("%d", answer[i]);
system("pause");
}
(all codes have been run correctly)
After testing, the running condition of the code is (the shortest time after multiple tests):
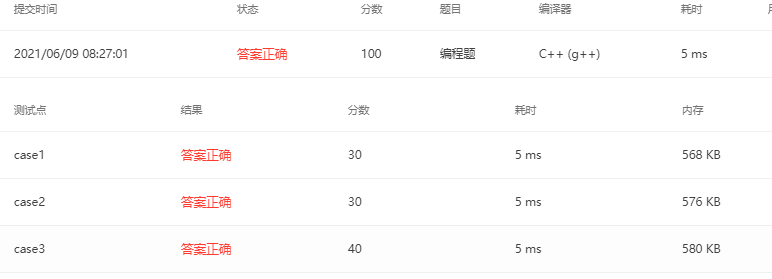
Topic 1 requirements
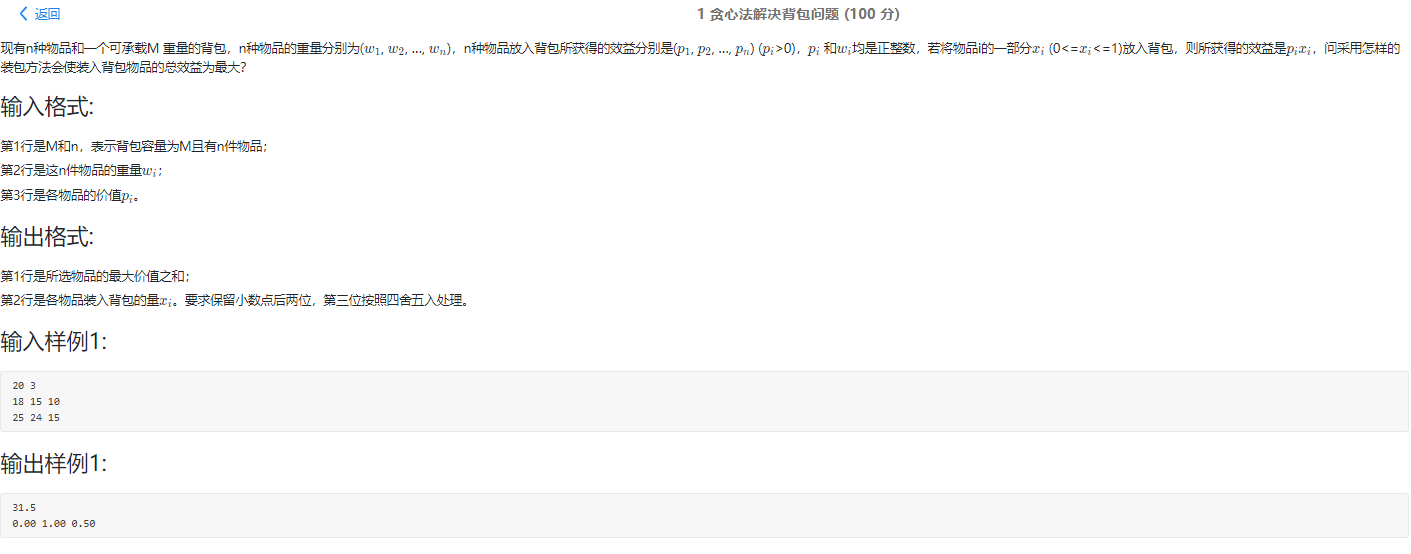
Overall thinking
For the complete knapsack problem, in order to maximize the benefit, I must give priority to the one with the largest value per unit volume, so find the value per unit volume and sort it from large to small.
code
#include <iostream>
#include <algorithm>
using namespace std;
struct mission {
double w;//quality
double v;//value
int idx;//Serial number
double val;//Unit mass value
bool operator < (const mission & node) const {
return val > node.val;//Guarantee from big to small
}
};
mission item[1000];
int m, n;
double ans = 0;
double answer[1000] = { 0 };
int main() {
cin >> m >> n;
for (int i = 1; i <= n; i++) {
cin >> item[i].w;
item[i].idx = i;
}
for (int i = 1; i <= n; i++) {
cin >> item[i].v;
item[i].val = (item[i].v) / item[i].w;//Find the value per unit mass
}
sort(item + 1, item + 1 + n);//Sort the unit mass value from large to small
for (int i = 1; i <= n; i++) {
if (m == 0) {//Don't pack when the backpack is full
continue;
}
double temp_w = item[i].w;//Take out the weight
if (m - temp_w >= 0) {//Can be completely put in
double temp1 = temp_w / item[i].w;//Find the ratio
answer[item[i].idx] = temp1;
ans += item[i].v*temp1;//Value * ratio (see the title for the formula)
m -= temp_w;//Update m
}
else {
double temp1 = m / item[i].w;//Find the ratio of the weight I can take away to the total
answer[item[i].idx] = temp1;
ans += item[i].v*temp1;//Use it to calculate the total value
m = 0;
}
}
printf("%g\n", ans);//Output, negligible
int i = 1;
for (; i < n; i++)
{
printf("%.2f ", answer[i]);
}
printf("%.2f", answer[i]);
system("pause");
return 0;
}
(all codes have been run correctly)
After testing, the running condition of the code is (the shortest time after multiple tests):
