Minimum circle coverage
There are multiple points on the plane. Find the smallest circle, which can cover all points.
Random increment method
Let's talk about the incremental method first.
The incremental method is applicable to an algorithm, and the sub problem can often be transferred to the original problem.
Randomizing the incremental method can avoid the most complex situation caused by data construction.
Practice 1 violence enumeration
The goal is to find the smallest circle, which can include all points.
The most violent way is to enumerate three points as points on the circle boundary, fix the circle at three points and take the largest circle.
Why is the largest circle?
If the existing point is not in the current maximum circle, to include this point, the current maximum circle must expand itself and then include it. (intuitively understand... The three points fix a circle, and the circle must increase the radius before it can be free...)
This complexity is O(n3)
Practice 2 random increment
Then if we add a point to a circle, or expand the circle, we can save a lot of complexity.
First, let's disrupt the points. (random increment)
First, select the first point as the initial circle O (radius 0) [that is, there is only one point].
Then triple cycle.
-
Enumerate each point i as the first boundary point.
If it is within the current circle, nothing will happen. continue. (do not enter cycle 2)
Otherwise, discard the current circle, set point i as the first boundary point, and the circle with the diameter formed by the first point as the current circle O, and enter cycle 2.
-
Enumerate each point j before i as the second boundary point.
If it is within the current circle, nothing will happen. continue. (do not enter cycle 3)
Otherwise, j is determined as the second boundary point, and the circle with the diameter composed of i and j enters cycle 3 as the current circle O.
-
Enumerate each point k before j as the third boundary point.
If it is within the current circle, nothing happens.
Otherwise, k is determined as the third boundary point and the three-point circle is determined as the current circle O.
The above is the algorithm steps.
The principle is explained as follows
Considering the first cycle, assuming that the point before i-1 completes the minimum circle coverage to obtain o through the above steps, but the point i is not in O, then we must reconstruct the circle, and i must be on the boundary of the new O (the "circle expansion theory" in practice 1), so i is taken as the first boundary point.
Now that the circle has been updated, look for the second update point
Considering the second cycle, if point j is not in the new circle, it means that j must be in the expanded circle and is a boundary point as the second boundary point.
The third cycle finds a point that is not in the new circle. It must also be the third boundary point. The three points determine a circle.
From top to bottom, triple circle.
Directly on the code.
#include <bits/stdc++.h>
using namespace std;
#define eps 1e-12
struct point
{
double x, y;
}a[100010], o;
double r;
double dis(point a, point b)
{
return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
point get_o(point p1, point p2, point p3)
{
double a1, b1, c1, a2, b2, c2;
a1 = 2 * (p1.x - p2.x);
b1 = 2 * (p1.y - p2.y);
c1 = (p1.x * p1.x - p2.x * p2.x + p1.y * p1.y - p2.y * p2.y);
a2 = 2 * (p1.x - p3.x);
b2 = 2 * (p1.y - p3.y);
c2 = (p1.x * p1.x - p3.x * p3.x + p1.y * p1.y - p3.y * p3.y);
point ans;
ans.x = (b2 * c1 - b1 * c2) / (a1 * b2 - b1 * a2);
ans.y = (c1 * a2 - c2 * a1) / (b1 * a2 - a1 * b2);
return ans;
}
int main()
{
int n;
cin >> n;
for (int i = 1; i <= n; ++i)
cin >> a[i].x >> a[i].y;
random_shuffle(a + 1, a + n + 1);
o = a[1], r = 0;
for (int i = 2; i <= n; ++i)
{
if (dis(o, a[i]) - r < eps)
continue;
o.x = (a[1].x + a[i].x) / 2;
o.y = (a[1].y + a[i].y) / 2;
r = dis(a[1], a[i]) / 2;
for (int j = 1; j < i; ++j)
{
if (dis(o, a[j]) - r < eps)
continue;
o.x = (a[i].x + a[j].x) / 2;
o.y = (a[i].y + a[j].y) / 2;
r = dis(a[i], a[j]) / 2;
for (int k = 1; k < j; ++k)
{
if (dis(o, a[k]) - r < eps)
continue;
o = get_o(a[i], a[j], a[k]);
r = dis(o, a[i]);
}
}
}
printf("%.10f\n", r);
printf("%.10f %.10f", o.x, o.y);
return 0;
}
I actually had questions in my own learning process.
Q: Every time you just take a point to form a circle, will you take the back point to form a circle and make the front point not in the circle?
A: No. Theoretically, the points taken each time are not in the current circle and must be boundary points, so the three-point circle construction is maximized.
And if there are four points ABCD, the current boundary points are D and C. If ACD configuration circle does not contain B and BCD configuration circle does not contain A, D will be included when ABC three-point configuration circle is taken, which is inconsistent with the selection of boundary points. As shown in the figure.
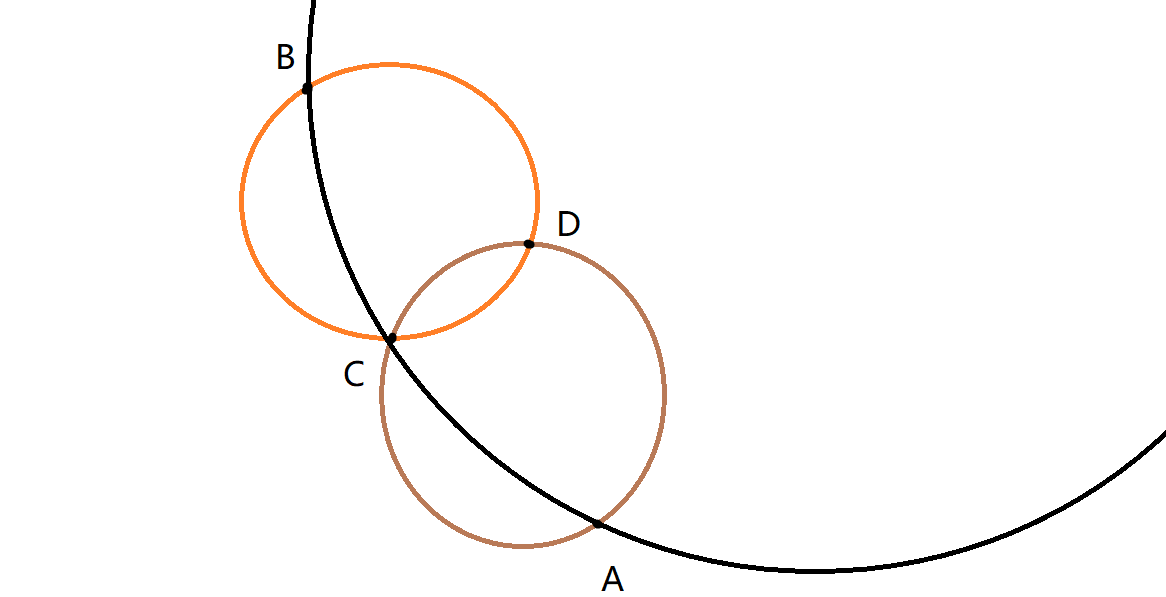
Therefore, we can rest assured and boldly use this expansion method.
Q: Three point common circle method
A: emmm, solve the three point series equations, Goo Goo.
Q: Complexity assurance
A: The first loop enumeration i and the second loop enumeration j may be in a circle, and the complexity is
Where g(i) is the complexity of the third cycle
The probability that each point is taken as a boundary point is \ (\ frac3i \)