I was so angry that I didn't see the minimum cut of 60 points in CSP T4
What is the minimum cut
---The following is a quote from God \ (\ mathrm {\ color {black} w} {\ color {red} {ind \ _whisper}} \)---
The so-called minimum cut is the minimum cut
(escape)
---The above is a quote from God \ (\ mathrm {\ color {black} w} {\ color {red} {ind \ _whisper}} \)---
We usually consider the minimum cut of the network with source and sink
For a network, all points are divided into two sets. One set contains source points and the other set contains sink points. Such a division scheme is called cut
Minimum cut is a partition scheme that minimizes the weight of broken edges
Supplement: minimum cut of passive sink
An edge breaking scheme that divides the whole network into exactly two subgraphs and minimizes the sum of edge breaking weights
It can be solved in approximate \ (\ mathrm{O}(n^3) \) time using stoer Wagner algorithm
How to find the minimum cut
Maximum flow minimum cut theorem
For a network, its minimum cut \ (c) (s, t)_ {\ min} \) is equal to its maximum flow \ (f(S,T)_{\max}\).
Therefore, with the blessing of this theorem, dinic can be used to find the minimum cut in \ (\ mathrm{O}(n^2m) \) time
But normally, it's obviously dissatisfied with running. It's really not good. Just HLPP
Examples
Only release the code of the drawing part, and directly connect your dinic with the minimum cut
T1
Find the minimum broken edge weight sum that makes the root of a tree with edge weight disconnected from each leaf
Because I can't write the tree DP, I directly consider the minimum cut
Obviously, the root is used as the source point, the leaf is connected to the super sink, and then the edge weight is used as the flow. The flow from the leaf to the sink is infinite (i.e. marked as non cuttable)
The code doesn't go away
T2
P1345 [USACO5.4] telecommunication of dairy cows
Find the minimum number of cut points that make two points of an undirected graph disconnected
Consider how to convert cutting edge into cutting point
Split points: convert a point into an in point and an out point. The in and out points are connected by edges with capacity of 1. For each edge \ ((s,t) \) of the original graph, convert it into
\The output point of (s \) is connected to the input point of \ (t \) and the output point of \ (t \) is connected to the input point of \ (s \), and the capacity is unlimited
int n = read(),m = read();s = read(),t = read();
s += n;
rep(i,1,n)
AddEdge(i,i + n,1);
rep(i,1,m) {
int st = read(),ed = read();
AddEdge(st + n,ed,INF);
AddEdge(ed + n,st,INF);
}
T3
P2944 [USACO09MAR]Earthquake Damage 2 G
It is similar to the previous question, that is, only some points need to be connected with meeting points
int n = read(),m = read(),p = read();s = 1 + n,t = (n << 1) + 1;
ff(i,1,m) {
int st = read(),ed = read();
AddEdge(st + n,ed,INF);
AddEdge(ed + n,st,INF);
}
ff(i,1,p) {
int st = read();
vis[st] = 1;
AddEdge(st + n,t,INF);
}
ff(i,1,n) if(!vis[i])
AddEdge(i,i + n,1);
else AddEdge(i,i + n,INF);
T4
P2057 [Show2007] goodwill voting / [JLOI2010] champion survey
The elements of the minimum cut classical model are divided into two sets
Let the source point represent one set and the sink point represent another set. For each conflict relationship, it is enough to build an edge with positive and negative capacity of 1 between the two people
int n = read(),m = read();s = 0,t = n + 1;
ff(i,1,n) {
int flag = read();
if(flag) AddEdge(s,i,1);
else AddEdge(i,t,1);
}
ff(i,1,m) {
int st = read(),ed = read();
AddEdge(st,ed,1),AddEdge(ed,st,1);
}
T5
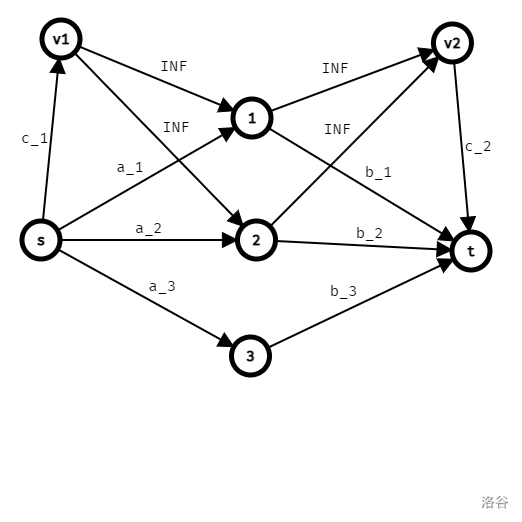
An article is divided into two sets with different values - > the source point represents set B, the value of set A is divided into this point, the sink point represents set B, and this point is connected to the sink point and divided into the value of set A
Consider how to realize that several crops can obtain certain value in the same set
The edge connected by the cut and the source point represents the set where the divide and sink points are located, so as long as two points are in the same set (i.e. connected with the source point or sink point at the same time), an edge that does not need to be cut can be established
Two virtual nodes are established. One represents the value that can be obtained by connecting the source point at the same time, that is, the edge with capacity of \ (c \) is connected from the source point to the virtual node, and the virtual node connects the edge with infinite capacity to multiple related crops
The other is the same, connecting the edge to the meeting point
As shown in the figure:
ll sum = 0;
ff(i,1,n) {
ll w = read();
AddEdge(s,i,w);
sum += w;
}
ff(i,1,n) {
ll w = read();
AddEdge(i,t,w);
sum += w;
}
int m = read();
ff(i,1,m) {
int cnt = read();
ll w1 = read(),w2 = read();
AddEdge(s,i * 2 - 1 + n,w1);
AddEdge(i * 2 + n,t,w2);
ff(j,1,cnt) {
int p = read();
AddEdge(i * 2 - 1 + n,p,1000000000);
AddEdge(p,i * 2 + n,1000000000);
}
sum += w1,sum += w2;
}
write(sum - dinic());
Finally, the total output value minus the minimum lost value
T6
Applying the technique of the previous question to the grid, the source and sink points still represent two sets, and each relationship can establish a virtual node
T7
P1935 [national training team] enclosure plan
From the adjacent same income in the previous question to the adjacent different income, it is obvious that the source sink point cannot be directly used to represent two sets
Consider direct black and white dyeing
The source point connects the edge with the capacity of \ (a {I, J} \) to the black dot and the edge with the capacity of \ (B {I, J} \) to the white dot
The black dot is connected to the edge with the capacity of \ (B {I, J} \), and the white dot is connected to the edge with the capacity of \ (a {I, J} \)
Then connect the edges with the capacity of \ (C {I, J} + C {I \ PM 1, J \ PM 1} \) between the black and white dots
In this way, when two adjacent points are connected with the source / sink point (i.e. divided into different sets), the edge connecting the two points can be continuously disconnected
inline void AddEdge(int st,int ed,int cap,int c2 = 0) {
e[++ecnt] = (Edge) {head[st],ed,cap},head[st] = ecnt;
e[++ecnt] = (Edge) {head[ed],st,c2},head[ed] = ecnt;
}
#define Node(x,y) ((x - 1) * m + y)
int mian() {
init_IO();
mems(head,-1);
ll sum = 0;
int n = read(),m = read();s = 0,t = n * m + 1;
ff(i,1,n) ff(j,1,m) {
int a = read();sum += a;
if((i + j) & 1) AddEdge(s,Node(i,j),a);
else AddEdge(Node(i,j),t,a);
}
ff(i,1,n) ff(j,1,m) {
int b = read();sum += b;
if(!((i + j) & 1)) AddEdge(s,Node(i,j),b);
else AddEdge(Node(i,j),t,b);
}
ff(i,1,n) ff(j,1,m) {
int c = read();
if(i > 1) AddEdge(Node(i,j),Node(i - 1,j),c,c),sum += c;
if(i < n) AddEdge(Node(i,j),Node(i + 1,j),c,c),sum += c;
if(j > 1) AddEdge(Node(i,j),Node(i,j - 1),c,c),sum += c;
if(j < m) AddEdge(Node(i,j),Node(i,j + 1),c,c),sum += c;
}
write(sum - dinic());
end_IO();
return 0;
}
T8
P1344 [USACO4.4] tracking down bad milk Pollutant Control
In addition to the minimum cut, the number of cut edges is also required
One way is to change the edge weight on the residual network and then find the maximum flow, but the capacity of this problem is very small
Consider multiplying the capacity of each edge by a large enough prime number and adding one, then the minimum cut is the minimum cut of the new graph, with that prime number, and the number of cut edges is the prime number of the minimum cut module of the new graph
T9
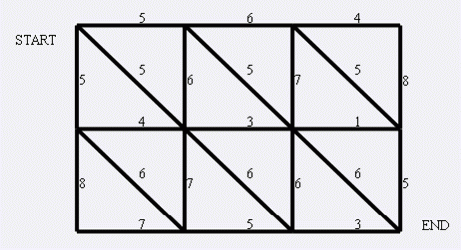
P4001 [ICPC Beijing 2006] wolf catches rabbit
At first glance, it seems to be the smallest cut, but in fact, the author is stuck with simple Dinic
However, the graph of this problem is not similar to the previous virtual node, but a plan graph
For a planar graph, its minimum cut can be transformed into the shortest path on the dual graph
For each closed area of the original drawing, regard it as a node, take the lower left as the starting point and the upper right as the end point, and make a diagonal from the original source point to the original sink point to divide the external area of the original drawing into two parts
If two closed areas have a common edge, connect the edge between the two points
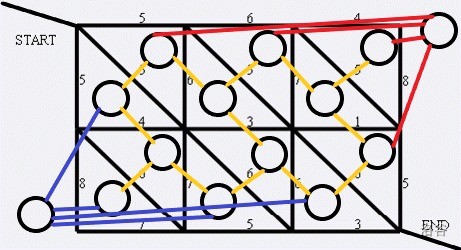
This is the complexity of \ (\ mathrm{O} (n^2 \log n^2) \)
T10
P7916 [CSP-S 2021] traffic planning
How to get 60 points
If the two adjacent ends are different, we have to pay a price, direct minimum cut
In addition, the author gives a good 3s time limit, and dinic on this dense map can get 60 points
It can be seen that the slowest point is only more than 600 milliseconds
How to get 80 points
Observe the range of test points. For test points 13 ~ 16,k = 2
So apply the problem of wolf catching rabbit above and try to make the shortest path of dual graph
(then you can just rely on T4 to get the first prize of the province, write for 1.5 hours and then put it away for 2.5 hours)
How to get full marks
Consider hlpp update 2022.1.26: hlpp is useless
James B Orlin's + KRT (King, Rao, Tarjan) algorithm considering \ (\ mathrm{O}(VE) \)
Consider putting it away
Consider continuing to expand from the shortest path
Obviously, after the super source point is established, the graph is not a plane graph and does not have the excellent property of running the shortest path after the dual graph is established
update : 2022.1.26
I promise to make it up in my next life!