Directory navigation:
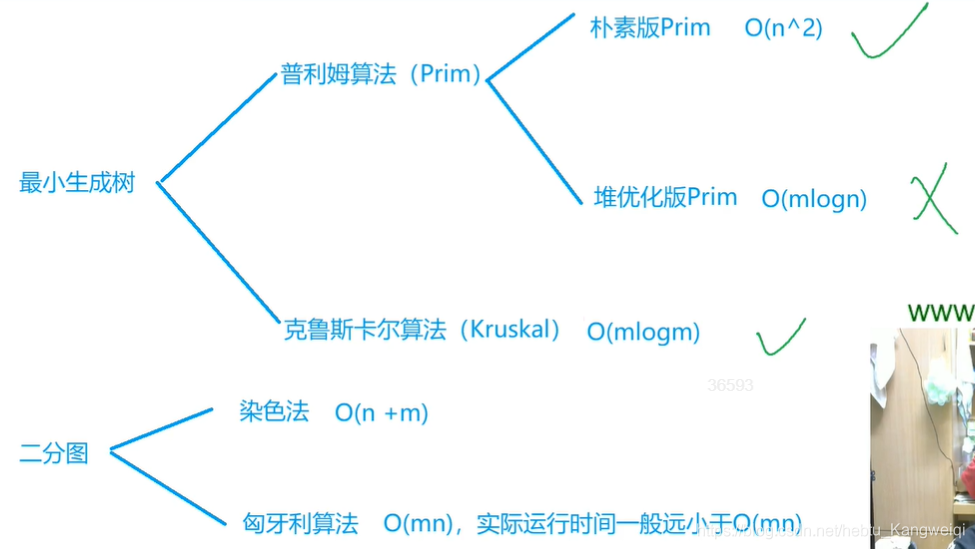
Minimum spanning tree:
For a graph with n points, the edges must be greater than or equal to n − 1. The minimum spanning tree is to select from these edges
N-1 edges connect all n points, and the sum of edge weights of these n − 1 edges is the smallest of all schemes
One more thing:
There are n points in the original graph, and the edges are larger than n-1. Delete the redundant edges to minimize the edge length of the remaining n-1 edges
Prim algorithm constructs minimum spanning tree
The diagram written by the great God is very vivid:
Minimum spanning tree_ ZhuRanCheng's blog - CSDN blog_ minimum spanning tree
To sum up: greedy algorithm
Select the smallest edge every time, put the smallest edge into the set I have updated, and use this set to update other points
Algorithm idea:
inf=0x3f3f3f3f//A large number
dist[i]<----inf//The initialization distance is a large number
for(i=0;i<n;i++)
{
t<----Find the point closest to the set outside the set
use t Update the distance from other points to the collection
st[t]=true//sign
}
Example:
Given an undirected graph with n points and m edges, there may be multiple edges and self rings, and the edge weight may be negative.
Find the sum of the tree edge weights of the minimum spanning tree. If the minimum spanning tree does not exist, output impossible.
Given an undirected graph with weighted edges, G=(V, E), where V represents the set of vertices in the graph and E represents the set of edges in the graph,
n=|V|,m=|E|.
An undirected connected subgraph composed of all n vertices in V and n-1 edges in E is called a spanning tree of G, and the spanning tree with the smallest sum of edge weights is called the smallest spanning tree of undirected graph G
If the two points are not connected, the minimum spanning tree cannot be generated
Code implementation:
#include <iostream>
#include <cstring>
using namespace std;
const int N = 510, INF = 0x3f3f3f3f;
int n, m;
int g[N][N], dist[N];//Dense graph
//The adjacency matrix stores all edges
//dist stores the distance from other points to S;
bool st[N];//Judgment array
int prim() {
//If the graph is disconnected, INF is returned; otherwise, res is returned
memset(dist, INF, sizeof dist);//The initialization distance is a large number
int res = 0;//result
for (int i = 0; i < n; i++)
{
int t = -1;//Any meaningless number is enough
for (int j = 1; j <= n; j++)
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
//Find the point closest to set S
if (i && dist[t] == INF) return INF;//The if is not executed after i=0 for the first time
//Judge whether it is connected and whether there is a minimum spanning tree
if (i) res += dist[t];//If I > 0 and the distance from t to set S is dist[t]
//cout << i << ' ' << res << endl;
st[t] = true;//sign
//Update the weights and of the latest S
for (int j = 1; j <= n; j++) dist[j] = min(dist[j], g[t][j]);//Different from dijstra algorithm:
}
return res;
}
int main() {
cin >> n >> m;//Number of points, number of sides
int u, v, w;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (i == j) g[i][j] = 0;//Heavy edge: initialize the distance to yourself to 0
else g[i][j] = INF;//Not for reprogramming: the distance of I - > J is initialized to INF
while (m--)//m edges
{
cin >> u >> v >> w;//The side length of U - > V is w
g[u][v] = g[v][u] = min(g[u][v], w);//Overwrite the side length of the original INF
}
int t = prim();//Receive return value
//Temporary storage prevents the function from executing twice, resulting in only 0 being returned in the end
if (t == INF) puts("impossible");//Description: unable to connect
else cout << t << endl;//Sum of output side lengths
}
Differences and relations between dijstra algorithm and dijstra algorithm:
You can see the same idea as the overall algorithm of ditra
The difference is that Dijkstra algorithm is the distance from the update to the starting point, and Prim is the distance from the update to the set S
In the code: for (int j = 1; J < = n; j + +) dist [J] = min (dist [J], G [t] [J]);
dijstra algorithm is:
For (int j = 1; J < = n; j + +) / / traverse point 1 to point n
dist[j] = min(dist[j], dist[t] + g[t][j]);// The distance of 1 ~ J points becomes: the distance of 1~t + the distance of t~j
Kruskal algorithm
The illustration of the algorithm is still recommended:
Minimum spanning tree_ ZhuRanCheng's blog - CSDN blog_ minimum spanning tree
Summary: still greedy!
Sort each side according to the side length, and the one with small side length is on the top! Then the shortest distance from an edge to an edge is obtained and connected in order, that is, those connected to the top first. In the process of edge adding construction, there may be a loop: 1 - > 2 - > 3 - > 1, which is not allowed. Therefore, skip this edge and do not select it. Finally, a minimum spanning tree without loop is formed!
Realize the following functions:
(1) Sort by side length
(2) Key point: judge whether adding this edge will form a loop
We can think of the connected block in the data structure section. As long as we prove that the ancestors of the two sides are the same, we will connect
(3) Add the edge to res and finally return to res
Code Description:
Algorithm idea:①Sorts all edges by weight from small to large ②Enumerate each edge a,b,Weight is c if a,b Disconnected Add this edge to the set
Example:
Given an undirected graph with n points and m edges, there may be multiple edges and self rings, and the edge weight may be negative.
Find the sum of the tree edge weights of the minimum spanning tree. If the minimum spanning tree does not exist, output impossible.
Given an undirected graph with weighted edges, G=(V, E), where V represents the set of points in the graph, E represents the set of edges in the graph, n=|V|, m=|E|.
An undirected connected subgraph composed of all n vertices in V and n-1 edges in E is called a spanning tree of G, in which the spanning tree with the smallest sum of edge weights is called the smallest spanning tree of undirected graph G.
Code implementation:
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 2e5 + 5;
int n, m;
struct Edge //Define structures to facilitate correspondence and sorting
{
int u, v, w;
bool operator<(const Edge& a) const //Preprocessing of sorting
{
return w < a.w;
}
}edge[N];
int p[N];
int find(int x)//And look for the same ancestors in the search set
{
return p[x] == x ? x : p[x] = find(p[x]);
}
int main()
{
int n, m;
scanf("%d%d", &n, &m);
for (int i = 0; i < m; i++)
{
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
edge[i] = { u,v,w };
}
sort(edge, edge + m);//Sort m edges
for (int i = 1; i <= n; i++) p[i] = i;//Storage node
int cnt = 0, sum = 0;//cnt: times sum: sum of side lengths
for (int i = 0; i < m; i++)//Traverse each edge
{
int a = edge[i].u, b = edge[i].v, w = edge[i].w;
a = find(a);//Find the ancestor node of a
b = find(b);//Find the ancestor node of b
if (a != b)//If the ancestral nodes are different: prove that a and b are not connected
{
cnt++;//Connect a and B, times++
sum += w;//Add side length to sum
p[a] = b;//Connect node a to node b
}
}
if (cnt < n - 1) puts("impossible");
else printf("%d", sum);
}
Core:
Understand that the ancestral nodes before connection are different and the same after connection. If it is 1 - > 2 - > 3 ^ 3 - > 1: we can't connect. Why? Because their ancestral nodes are the same, skip this case, which perfectly implements the Kruskal algorithm
Bipartite graph
Important conclusion: a graph is a bipartite graph if and only if the graph does not contain odd rings
(1) Judgement bipartite graph by coloring method
Question:
Given an undirected graph with n points and m edges, there may be multiple edges and self rings in the graph.
Please judge whether this graph is a bipartite graph
Illustration:
Overview: dye the starting point as 1, and the dot dye connected to the starting point as 2, and so on. The colors of adjacent dot dyes cannot be the same. If there is no conflict, the graph is a bipartite graph. If there is a conflict, the graph is not a bipartite graph
Deep first search approach:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 1e5 + 10, M = 2e5 + 10;
int n, m;
int h[N], e[M], ne[M], idx; //Storage of adjacency table
int color[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool dfs(int u, int c)
{
color[u] = c; //The current color of this point u is c
for (int i = h[u]; i != -1; i = ne[i])//Traversal of linked list
{
int j = e[i];//Record node
if (!color[j]) //The adjacency point j of u is not stained
{
dfs(j, 3 - c); // If the color of u is 1, j is 3-1 = 2; If the color of u is 2, j is 3-2 = 1
}
else if (color[j] == c) return false; //Two adjacent dots are dyed in the same color
}
return true;
}
int main()
{
cin >> n >> m;
memset(h, -1, sizeof(h));
while (m--)
{
int a, b;
scanf("%d%d", &a, &b);
add(a, b), add(b, a); // An undirected graph creates two edges in opposite directions
}
bool flag = true;
for (int i = 1; i <= n; i++) //Traverse all points of the graph
if (!color[i])//Unstained
{
if (!dfs(i, 1))//Dye node 1 with color 1 and dye it downward: if the result returned by dfs is false, flag=false will be marked
{
flag = false;
break;
}
}
if (flag) cout << "Yes";
else cout << "No";
}
Breadth first search approach:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
typedef pair<int, int> PII; //first save point number, second save color
const int N = 1e5 + 10, M = 2e5 + 10;
int n, m;
int h[N], e[M], ne[M], idx; //Storage of adjacency table
int color[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool bfs(int u)
{
queue<PII> q;
q.push({ u,1 });//Join the team
color[u] = 1; //The current color of this point u is c
while (q.size()) //Queue is not empty
{
PII t = q.front();
q.pop();//Take out the head of the team
int ver = t.first, c = t.second;
for (int i = h[ver]; i != -1; i = ne[i])//Traversal linked list
{
int j = e[i];
if (!color[j]) //Not stained
{
color[j] = 3 - c;
q.push({ j,3 - c });//Join the team
}
else if (color[j] == c) return false; //Two adjacent dots are dyed in the same color
}
}
return true;
}
int main()//The same framework as dfs
{
cin >> n >> m;
memset(h, -1, sizeof(h));
while (m--)
{
int a, b;
scanf("%d%d", &a, &b);
add(a, b), add(b, a); // An undirected graph creates two edges in opposite directions
}
bool flag = true;
for (int i = 1; i <= n; i++) //Traverse all points of the graph
if (!color[i])
{
if (!bfs(i))
{
flag = false;
break;
}
}
if (flag) cout << "Yes";
else cout << "No";
}
Error prone:
The storage of single linked lists does not have to be connected in order. For example:
Tree structure:
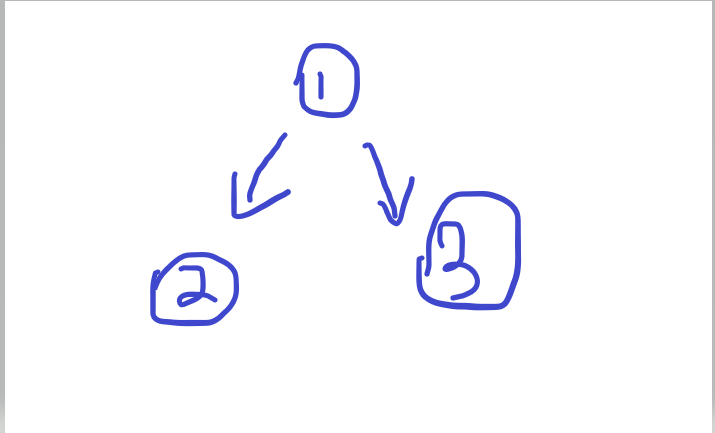
Structure stored in single linked list:

The difference from dfs lies in the connection order of the single linked list. The focus is to build a simulated dfs and bfs in your mind
hungarian algorithm
Algorithm idea:
Specific example: brother, I like that girl. Why don't you change another girl who likes you? Let me come
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 510, M = 1e5 + 10;
int n1, n2, m;
int h[N], e[M], ne[M], idx; //Adjacency table
int match[N];
bool st[N];
void add(int a, int b)//a->b
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool find(int x)
{
for (int i = h[x]; i != -1; i = ne[i]) // Boys like all girls
{
int j = e[i];
if (!st[j]) // If st[j] = true, the girl will not be considered
{
st[j] = true; // Mark j this girl. The function is that if this girl has a boyfriend, we don't need to consider his current object j when we find out if her boyfriend is possible to be with other girls
if (match[j] == 0 || find(match[j]))// The girl has no object or the girl's boyfriend can be with other girls she likes
{
match[j] = x; //Match successful
return true;
}
}
}
return false;
}
int main()
{
cin >> n1 >> n2 >> m;
memset(h, -1, sizeof(h));
while (m--)
{
int a, b;
scanf("%d%d", &a, &b);
add(a, b); //It's enough to save only one boy to the girl
}
int res = 0; // Number of current matches
for (int i = 1; i <= n1; i++) // Traverse every boy
{
memset(st, false, sizeof(st)); //The representative of girls has not been considered yet. Each girl only considers it once
if (find(i)) res++; // The boy matched
}
cout << res;
}