Background: Recently, I have been attacked mentally. I often doubt my life. When I doubt my life, I always write a cool algorithm. Today, I will introduce Kurskal algorithm, the algorithm of the minimum spanning tree of a graph, to my friends;
...
Because the literary talent of the ape is not so good, it's not a long story. All the stories are in the code:
package ALG;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Scanner;
/**
* Minimum spanning tree: Kruskal algorithm;
*
* Thoughts:
* 1.Sort the edges and find two nodes according to their weights;
* 2.If the loop is formed, continue to search;
*
* */
public class Kruskal {
// For storing all sides;
private static List<Edge> edges = new ArrayList<>();
// The endpoint used to record the current node;
private static HashMap<Character, Character> ed = new HashMap<>();
static Scanner input = new Scanner(System.in);
// As an internal class, edge attributes: weight, start, end;
static class Edge {
int weight;
char start;
char end;
Edge(char start, char end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
}
public static void main(String[] args) {
// Initialize, create a graph;
createGraph();
// Here, we use fast sorting to sort the edges from small to large according to the weight (other sorts can be used);
quickSortGraph(edges);
// Initialization, record the current state of the node, and set initialization as itself;
for (Edge edge : edges) {
ed.put(edge.start, edge.start);
ed.put(edge.end, edge.end);
}
// A node for storing the minimum spanning tree;
List<Edge> result = new ArrayList<>();
// Kruskal algorithm is used to generate the minimum spanning tree;
result = kruskal(edges, ed);
// Record the sum of the weights of the minimum spanning tree;
int minWeight = 0;
for (Edge edge : result) {
minWeight += edge.weight;
System.out.print("( " + edge.start + "," + edge.end + " )\t");
}
System.out.println("the min weight: " + minWeight);
}
private static List<Edge> kruskal(List<Edge> edges, HashMap<Character, Character> ed) {
List<Edge> result = new ArrayList<>();
for (Edge edge : edges) {
// To determine whether a loop will be generated, the method is as follows:
// If the end point of start is the same as the end point, it is proved that a loop will be generated at this time, and return false;
// Otherwise, the circuit will not be generated;
if (checkEdgeStatus(edge.start, edge.end, ed)) {
// When no loop is generated, this node is one of the nodes in the minimum spanning tree;
result.add(edge);
// Change the end positions of all nodes;
changeAllEnd(ed, edge.start, edge.end);
}
}
return result;
}
private static void changeAllEnd(HashMap<Character, Character> ed, char start, char end) {
// Save the end point of start with pivot, which is used to update the end point of all points whose end point is pivot
char pivot = ed.get(start);
for (Character key : ed.keySet()) {
if (ed.get(key) == pivot) {
ed.put(key, ed.get(end));
}
}
}
private static boolean checkEdgeStatus(char start, char end, HashMap<Character, Character> ed) {
// Check whether the end points of start and end are the same;
char point1 = ed.get(start);
char point2 = ed.get(end);
return point1 != point2;
}
// Next, the algorithm of fast sorting (divide and conquer, recursion);
private static void quickSortGraph(List<Edge> edges) {
quickSort(edges, 0, edges.size() - 1);
}
private static void quickSort(List<Edge> edges, int start, int end) {
int pivot;
while(start < end) {
pivot = quick(edges, start, end);
quickSort(edges, start, pivot - 1);
start = pivot + 1;
}
}
private static int quick(List<Edge> edges, int start, int end) {
Edge key = edges.get(start);
while(start < end) {
Edge edge;
while (start < end && edges.get(end).weight >= key.weight) {
end --;
}
edge = edges.get(end);
edges.set(start, edge);
while(start < end && edges.get(start).weight <= key.weight) {
start ++;
}
Edge edge1;
edge1 = edges.get(start);
edges.set(end, edge1);
}
edges.set(start, key);
return start;
}
// Create a map;
private static void createGraph() {
while(true) {
char start = input.next().charAt(0);
char end = input.next().charAt(0);
int weight = input.nextInt();
if (weight == -1) {
break;
}
edges.add(new Edge(start, end, weight));
}
}
// Print information on all sides
private static void printGraph(List<Edge> edges) {
for (Edge edge : edges) {
System.out.println(edge.start + "-" + edge.end + "-" + edge.weight);
}
}
}
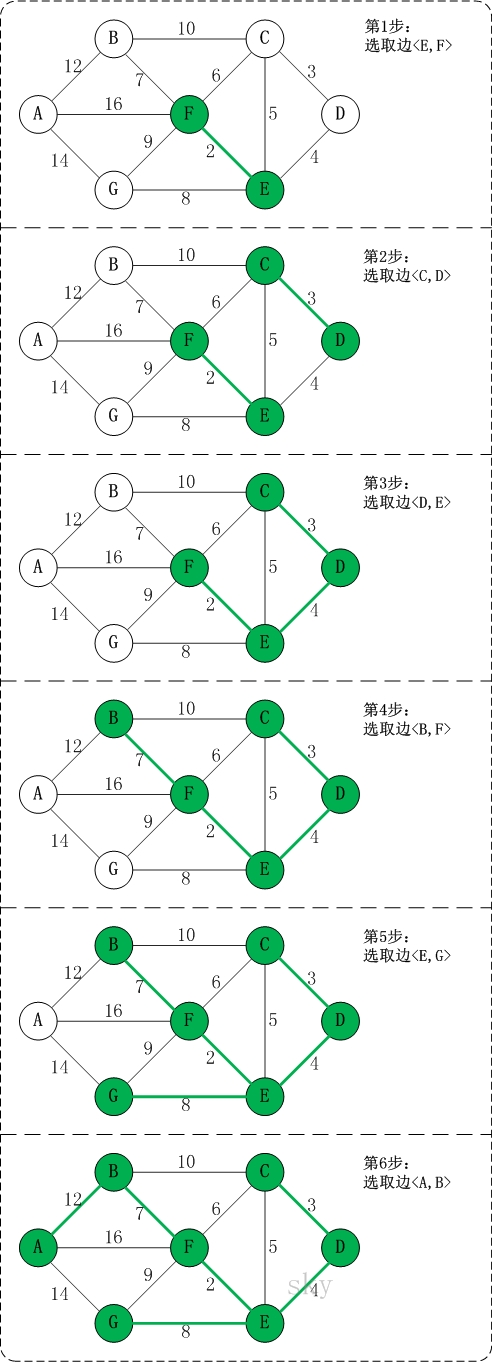
Operation result:

The next article will introduce another algorithm of minimum spanning tree: Prim algorithm