Yan's dp analysis
Learn the algorithm on AcWing, y is always strong! ha-ha
When using this method to solve the dp problem, the introduction is clear, that is, thinking about the dp problem from the perspective of set. The following is an example of the 01 knapsack problem
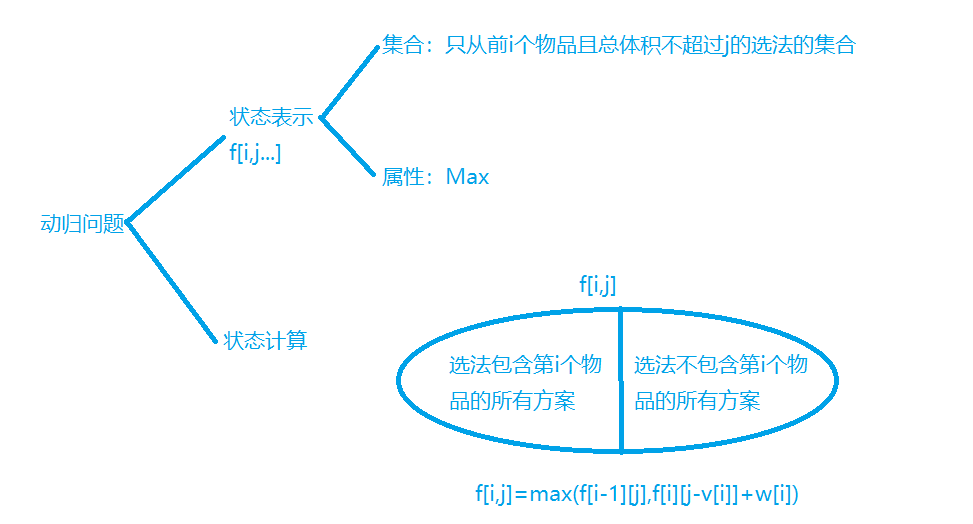
When thinking about a DP problem, we can think about the problem from two perspectives: state representation and state calculation. We should think about the problem from the perspective of set, that is, each state represents a kind of situation. Each term of the method is explained as follows:
Set: consider how many dimensions the set subscript consists of (generally from low dimension to high dimension), and determine the meaning represented by each dimension.
Attribute: the meaning of stored values in each state, generally including max, min and quantity.
State calculation: divide the set into several blocks in different situations, and calculate the value of each block (the curve can save the country), and solve the final value from all parts.
Backpack DP
Knapsack model is a classic model in dynamic programming. Its problem can generally be described as buying a variety of items to find their maximum value, the number of maximum value schemes, specific schemes and so on. Each item may have a variety of expenses (for example, there are restrictions on the total volume, total weight and total price, which can be abstracted into three expenses), and the goal is to have the highest total value. The coding idea of general knapsack problem is as follows:
initialization for Enumerate items for Enumerating expenses Enumeration decision Output answer
Backpack models can be divided into the following five types according to the quantity of the same kind of goods purchased and the restrictions of commodity combination.
01 Backpack
As the name suggests, 01 backpack has only two states, buy and don't buy.
Example: 01 knapsack problem
There are N items and a backpack with a capacity of V. Each item can only be used once.
The volume of article i is vi and the value is wi.
Solve which items are loaded into the backpack, so that the total volume of these items does not exceed the backpack capacity, and the total value is the largest. Output maximum value.
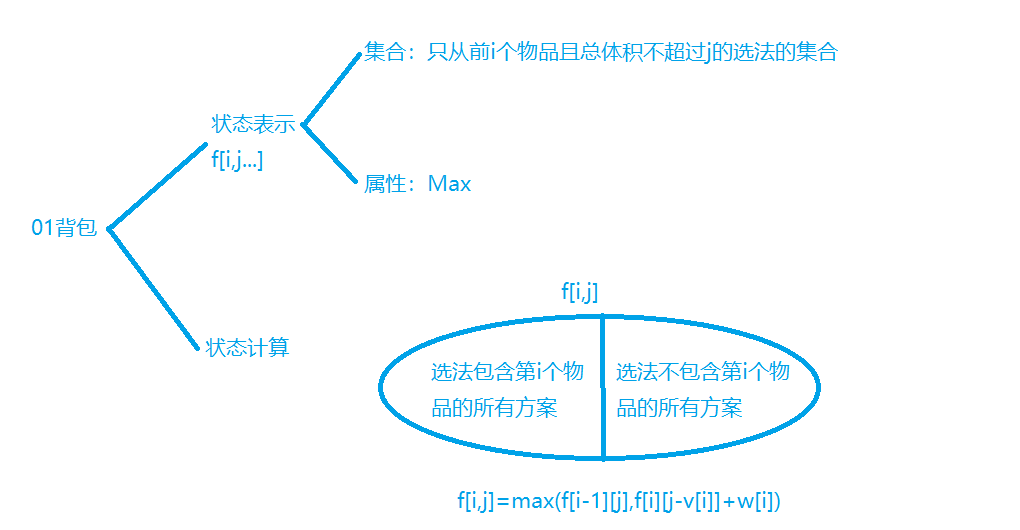
General knapsack problems can be stored in dimension reduction, but only a simple version is given here for ease of understanding. For dimension reduction storage, please see space optimization
const int N=1009;
int dp[N][N];
int main()
{
int n,m;
cin>>n>>m;
int vi,wi;
for(int i=1;i<=n;i++)
{
cin>>vi>>wi;
for(int j=1;j<=m;j++)
{
dp[i][j]=dp[i-1][j];
if(j-vi>=0)
dp[i][j]=max(dp[i][j],dp[i-1][j-vi]+wi);
}
}
cout<<dp[n][m];
return 0;
}
Examples and variants:
1. Ordinary 01 backpack: acwing: 01 knapsack problem
2. Two dimensional cost problem: acwing: 1022. Collection of pet elves
3. Number of schemes: acwing: 278. Digital combination
4. Greed + dp: acwing: energy stone
Complete Backpack
Number of schemes: acwing: 1023. Buy books
Greedy + complete backpack: acwing: 532. Monetary system
Multiple Backpack
Combined Backpack
Hybrid Backpack
Several common problems
Charge limit for status
There are three scenarios for the cost of a status: the scenario where the cost is not greater than j, the scenario where the cost is equal to j, and the scenario where the minimum cost is J. For the differences between these three cases, take 01 knapsack as an example, and other knapsack problems are similar.
- When the volume does not exceed v
Example: 01 knapsack problem
There are N items and a backpack with a capacity of V. Each item can only be used once. The volume of article i is vi and the value is wi. Solve which items are loaded into the backpack, so that the total volume of these items does not exceed the backpack capacity, and the total value is the largest. Output maximum value.
Analysis: the problem is called 01 knapsack problem. f(i, j) means that the volume of the first i items does not exceed the maximum value of j. no special operation is required during coding, and all initialization can be 0
//Note that this is a simple writing method without space optimization. dp array is a global variable, and all values are 0 by default.
#include<bits/stdc++.h>
using namespace std;
const int N=1009;
int dp[N][N];
int main()
{
int n,m;
cin>>n>>m;
int vi,wi;
for(int i=1;i<=n;i++)
{
cin>>vi>>wi;
for(int j=1;j<=m;j++)
{
dp[i][j]=dp[i-1][j];
if(j-vi>=0)
dp[i][j]=max(dp[i][j],dp[i-1][j-vi]+wi);
}
}
cout<<dp[n][m];
return 0;
}
- When the volume is equal to v
Example: acwing1023. Buy books
Xiao Ming has n yuan in his hand, all of which are used to buy books. The price of books is 10 yuan, 20 yuan, 50 yuan and 100 yuan. How many kinds of book buying schemes does Xiao Ming have? (multiple copies of each book can be purchased)
Analysis: this problem is called 01 knapsack problem to find the number of schemes. DP (i, j) is defined as the number of currencies in i that can exactly form the face value of j before use. During initialization, only the legal status is set as the set of legal values, and the illegal status is set as the illegal value (generally, the illegal value is - INF when calculating the maximum value, and vice versa, and 1 when calculating the number of schemes)
#include<bits/stdc++.h>
using namespace std;
const int N=1009;
int dp[5][N];
int v[5]={0,10,20,50,100};
int main()
{
int n;
cin>>n;
dp[0][0]=1//Note initialization
for(int i=1;i<=4;i++)
{
for(int j=0;j<=n;j++)
{
dp[i][j]=dp[i-1][j];
if(j-v[i]>=0) dp[i][j]+=dp[i][j-v[i]];
}
}
cout<<dp[4][n];
return 0;
}
- When the minimum volume is v
Example: acwing1020. diver
Divers use special equipment for diving. He has a cylinder with two gases: one is oxygen and the other is nitrogen. Various amounts of oxygen and nitrogen are required to get the diver to the depth. Divers have a certain number of cylinders. Each cylinder has weight and gas capacity. A diver needs a certain amount of oxygen and nitrogen to complete his work. What is the minimum total weight of the cylinders he needs to complete the work?
Analysis: firstly, the problem is called two-dimensional cost problem. The cost status should be defined as the minimum usage quantity. DP (i, j, k) represents the minimum weight selected in the first i cylinders with an oxygen volume of at least j and a nitrogen volume of at least k. You only need to set the selected negative value status to 0 when calculating the state transition
#include<bits/stdc++.h>
using namespace std;
int dp[1009][29][90];
int main()
{
int m,n,k;
cin>>m>>n>>k;
memset(dp,0x3f,sizeof dp);//Note initialization
dp[0][0][0]=0;
int ai,bi,ci;
for(int i=1;i<=k;i++)
{
cin>>ai>>bi>>ci;
for(int j=0;j<=m;j++)
{
for(int l=0;l<=n;l++)
{
int &x=dp[i][j][l];
x=dp[i-1][j][l];
x=min(x,dp[i-1][max(0,j-ai)][max(0,l-bi)]+ci);//Negative value set to 0
}
}
}
cout<<dp[k][m][n];
return 0;
}
Number of schemes and specific schemes
The problem of the number of solutions can be roughly divided into the number of solutions to solve the maximum value, the number of solutions to solve a certain cost, and the specific combination of solutions to solve the maximum value.
- Number of maximum value schemes
Example: acwing:11. Solution number of knapsack problem
There are N items and a backpack with a capacity of V. Each item can only be used once. The volume of article i is vi and the value is wi. Solve which items are loaded into the backpack, so that the total volume of these items does not exceed the backpack capacity, and the total value is the largest. Output the number of schemes of the most preferred method. Note that the answer may be very large. Please output the result of answer module 109 + 7.
Analysis: the problem is called 01 knapsack problem. First, we need to solve the maximum value when the volume is v. when solving the maximum value, we can maintain an array and record the transfer state. DP (i, J) represents the maximum value when only the first i items are used and the maximum volume is J. G (i, J) indicates that only the first i items are used, the maximum volume is j, and the value is the number of DP (i, J) schemes.
#include<bits/stdc++.h>
using namespace std;
const int N=1009,MOD=1e9+7;
int dp[N][N],g[N][N];
int main()
{
int n,v;
cin>>n>>v;
for(int i=0;i<=n;i++) g[i][0]=1;
for(int i=1;i<=n;i++)
{
int vi,wi;
cin>>vi>>wi;
for(int j=0;j<=v;j++)
{
dp[i][j]=dp[i-1][j];
g[i][j]=max(1,g[i-1][j]);
if(j-vi>=0)
{
dp[i][j]=max(dp[i][j],dp[i-1][j-vi]+wi);
if(dp[i-1][j-vi]+wi==dp[i-1][j]) g[i][j]=(g[i-1][j-vi]+g[i-1][j])%MOD;
if(dp[i-1][j-vi]+wi>dp[i-1][j]) g[i][j]=g[i-1][j-vi];
}
}
}
cout<<g[n][v];
return 0;
}
- Number of schemes for a certain expense
Example: acwing: 278. Digital combination
Given N positive integers A1,A2,..., AN, select several numbers from them, make their sum M, and find how many options there are.
Analysis: this question is a 01 knapsack model. dp (i, j) indicates the number of schemes with the value of j selected only from the first i. You only need to set the legal state of layer 0 of dp array to 1, and add the number of schemes in each direction during state transition.
#include<bits/stdc++.h>
using namespace std;
int dp[109][10009],w[109];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>w[i];
for(int i=0;i<=n;i++) dp[i][0]=1;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
dp[i][j]=dp[i-1][j];
if(j-w[i]>=0) dp[i][j]+=dp[i-1][j-w[i]];
}
}
cout<<dp[n][m];
return 0;
}
- Specific scheme combination for solving the maximum value
Example: acwing:12. Knapsack problem for specific solutions
There are n items and a backpack with a capacity of V. Each item can only be used once. The volume of article i is vi and the value is wi. Solve which items are loaded into the backpack, so that the total volume of these items does not exceed the backpack capacity, and the total value is the largest. The scheme of minimum output dictionary order. The dictionary order here refers to the sequence composed of the numbers of the selected items. The item number range is 1... N.
Analysis: firstly, the problem is called 01 knapsack problem, which allows the output of a maximum value scheme with minimum dictionary order. Here, we can use the method of backward state transition to solve it (note that the longer the dictionary order is, the larger the dictionary order is)
#include<bits/stdc++.h>
using namespace std;
const int N=1009;
int dp[N][N];
int v[N],w[N];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
for(int i=n;i>0;i--)
{
for(int j=1;j<=m;j++)
{
dp[i][j]=dp[i+1][j];
if(j-v[i]>=0) dp[i][j]=max(dp[i][j],dp[i+1][j-v[i]]+w[i]);
}
}
int j=m;
for(int i=1;i<=n;i++)
{
if(j-v[i]>=0&&dp[i][j]==dp[i+1][j-v[i]]+w[i])
{
j=j-v[i];
cout<<i<<' ';
}
}
return 0;
}
Path DP
Sequence DP
State machine DP
In a certain class of DP problems, there are many state types and certain transformation relations. At this time, we can consider whether we can adopt the state machine model.
Example: acwing:1058. Stock trading V
Given an array of length N, the ith number in the array represents the price of a given stock on day i. Design an algorithm to calculate the maximum profit. Under the following constraints, you can complete as many transactions as possible (buying and selling a stock multiple times): you can't participate in multiple transactions at the same time (you must sell the previous stock before buying again).
Analysis: firstly, it can be found that the problem has three states, and each state has a corresponding transition mode, so the solution method of state machine DP can be used here. The state transition diagram is as follows:
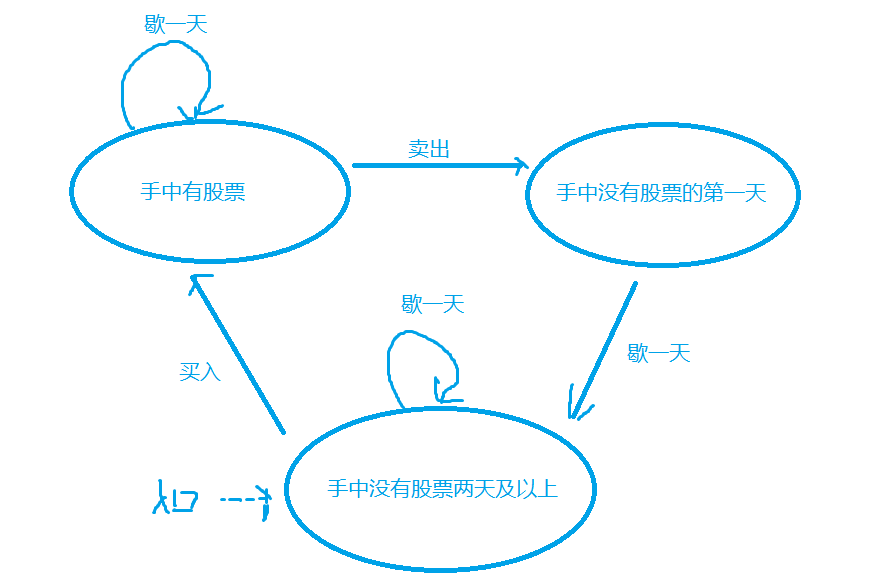
#include<bits/stdc++.h>
using namespace std;
int dp[100009][3];
int main()
{
int n;
cin>>n;
int x;
memset(dp,-0x3f,sizeof dp);
dp[0][2]=0;
for(int i=1;i<=n;i++)
{
cin>>x;
dp[i][0]=max(dp[i-1][2]-x,dp[i-1][0]);
dp[i][1]=dp[i-1][0]+x;
dp[i][2]=max(dp[i-1][2],dp[i-1][1]);
}
cout<<max(dp[n][1],dp[n][2]);
return 0;
}
Examples and variants:
1,acwing:1057. Stock trading IV
2,acwing:1052. Design password