Article directory
matplotlib Tutorial notes
cycler
Before we start the tutorial, we need to understand the cycle module
from __future__ import print_function
from cycler import cycler
color_cycler = cycler(color=["r", "g", "b"]) #You can create a cycle object with cycle color_cycler
| 'color' |
|---|
| 'r' |
| 'g' |
| 'b' |
len(color_cycler) #Get length
3
color_cycler.keys #Get key
{'color'}
from __future__ import print_function
for v in color_cycler: print(v)
{'color': 'r'}
{'color': 'g'}
{'color': 'b'}
cycler(ec=color_cycler) #You can use the existing cycle object as a parameter of cycle and return the same object
| 'ec' |
|---|
| 'r' |
| 'g' |
| 'b' |
for i in range(5): #It's going to be a mistake, obviously print(color_cycler[i])
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-9-b6d40aff26d1> in <module>
1 for i in range(5): #It's going to be a mistake, obviously
----> 2 print(color_cycler[i])
C:\Ana\lib\site-packages\cycler.py in __getitem__(self, key)
221 for k, v in six.iteritems(trans)))
222 else:
--> 223 raise ValueError("Can only use slices with Cycler.__getitem__")
224
225 def __iter__(self):
ValueError: Can only use slices with Cycler.__getitem__
cc = color_cycler() for j, c in zip(range(5), cc): #In this way, we can actually get an infinite sequence print(j, c)
0 {'color': 'r'}
1 {'color': 'g'}
2 {'color': 'b'}
3 {'color': 'r'}
4 {'color': 'g'}
#The sum of two cycle objects will be combined in a way of "inner product" lw_cycler = cycler(lw=range(1, 4)) #Notice len (LW cycle) = = 3 wc = lw_cycler + color_cycler #If they are different in length, they cannot be added print(len(wc)) print(wc.keys) for s in wc: print(s)
3
{'lw', 'color'}
{'lw': 1, 'color': 'r'}
{'lw': 2, 'color': 'g'}
{'lw': 3, 'color': 'b'}
#And are exchangeable lw_c = lw_cycler + color_cycler c_lw = color_cycler + lw_cycler for j, (a, b) in enumerate(zip(lw_c, c_lw)): print("({j}) A: {A!r} B:{B!r}".format( j=j, A=a, B=b ))
(0) A: {'lw': 1, 'color': 'r'} B:{'color': 'r', 'lw': 1}
(1) A: {'lw': 2, 'color': 'g'} B:{'color': 'g', 'lw': 2}
(2) A: {'lw': 3, 'color': 'b'} B:{'color': 'b', 'lw': 3}
#Similar operations can be done by passing in multiple parameters of equal length at one time wc = cycler(c=['r', 'g', 'b'], lw=range(1,4)) for s in wc: print(s)
{'c': 'r', 'lw': 1}
{'c': 'g', 'lw': 2}
{'c': 'b', 'lw': 3}
# Multiplication is similar to the definition of "outer product", that is to say, let's take a look at each of them m_cycler = cycler(marker=['s', 'o']) m_c = m_cycler * color_cycler print(len(m_c)) print(m_c.keys) for s in m_c: print(s)
6
{'marker', 'color'}
{'marker': 's', 'color': 'r'}
{'marker': 's', 'color': 'g'}
{'marker': 's', 'color': 'b'}
{'marker': 'o', 'color': 'r'}
{'marker': 'o', 'color': 'g'}
{'marker': 'o', 'color': 'b'}
#The two are not necessarily the same after multiplication exchange c_m = color_cycler * m_cycler for j, (a, b) in enumerate(zip(c_m, m_c)): print("({j}) A: {A!r} B: {B!r}".format( j=j, A=a, B=b ))
(0) A: {'color': 'r', 'marker': 's'} B: {'marker': 's', 'color': 'r'}
(1) A: {'color': 'r', 'marker': 'o'} B: {'marker': 's', 'color': 'g'}
(2) A: {'color': 'g', 'marker': 's'} B: {'marker': 's', 'color': 'b'}
(3) A: {'color': 'g', 'marker': 'o'} B: {'marker': 'o', 'color': 'r'}
(4) A: {'color': 'b', 'marker': 's'} B: {'marker': 'o', 'color': 'g'}
(5) A: {'color': 'b', 'marker': 'o'} B: {'marker': 'o', 'color': 'b'}
#Integer multiplication seems to simply multiply by several times color_cycler * 2 # == 2 * color_cycler
| 'color' |
|---|
| 'r' |
| 'g' |
| 'b' |
| 'r' |
| 'g' |
| 'b' |
color_cycler.concat(color_cycler) #Follow up concat
| 'color' |
|---|
| 'r' |
| 'g' |
| 'b' |
| 'r' |
| 'g' |
| 'b' |
color_cycler.concat(m_cycler) #It seems that concat must have the same key
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-18-c4ba2b85481a> in <module>
----> 1 color_cycler.concat(m_cycler) #It seems that concat must have the same key
C:\Ana\lib\site-packages\cycler.py in concat(self, other)
423 The concatenated `Cycler`
424 """
--> 425 return concat(self, other)
426
427
C:\Ana\lib\site-packages\cycler.py in concat(left, right)
459 just_one=left.keys ^ right.keys)
460
--> 461 raise ValueError(msg)
462
463 _l = left.by_key()
ValueError: Keys do not match:
Intersection: set()
Disjoint: {'marker', 'color'}
# Slicing operation color_cycler[::-1] #Reverse order
| 'color' |
|---|
| 'b' |
| 'g' |
| 'r' |
color_cycler[:2]
| 'color' |
|---|
| 'r' |
| 'g' |
color_cycler[1:]
| 'color' |
|---|
| 'g' |
| 'b' |
#We can view it by the "by key" method. The feeling is to get a key and its value c_m.by_key()
{'marker': ['s', 'o', 's', 'o', 's', 'o'],
'color': ['r', 'r', 'g', 'g', 'b', 'b']}
#This dictionary can be used as a blueprint for creating a new cycler bk = c_m.by_key() bk['color'] = ['green'] * len(c_m) cycler(**bk)
| 'color' | 'marker' |
|---|---|
| 'green' | 's' |
| 'green' | 'o' |
| 'green' | 's' |
| 'green' | 'o' |
| 'green' | 's' |
| 'green' | 'o' |
Some examples
from itertools import cycle import matplotlib.pyplot as plt from cycler import cycler import numpy as np
fig, (ax1, ax2) = plt.subplots(1, 2, tight_layout=True, figsize=(8, 4)) x = np.arange(10) color_cycler = cycler(c=["r", "g", "b"]) for i, sty in enumerate(color_cycler): ax1.plot(x, x*(i+1), **sty) for i, sty in zip(range(1, 5), cycle(color_cycler)): ax2.plot(x, x*i, **sty)
C:\Ana\lib\site-packages\matplotlib\figure.py:2366: UserWarning: This figure includes Axes that are not compatible with tight_layout, so results might be incorrect.
warnings.warn("This figure includes Axes that are not compatible "
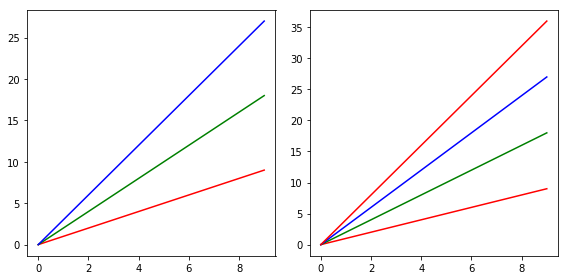
This example uses multiplication
fig, (ax1, ax2) = plt.subplots(1, 2, tight_layout=True, figsize=(8, 4)) x = np.arange(10) color_cycle = cycler(c=['r', 'g', 'b']) ls_cycle = cycler('ls', ['-', '--']) lw_cycle = cycler('lw', range(1, 4)) sty_cycle = ls_cycle * (color_cycle + lw_cycle) for i, sty in enumerate(sty_cycle): ax1.plot(x, x*(i+1), **sty) sty_cycle = (color_cycle + lw_cycle) * ls_cycle for i, sty in enumerate(sty_cycle): ax2.plot(x, x*(i+1), **sty)
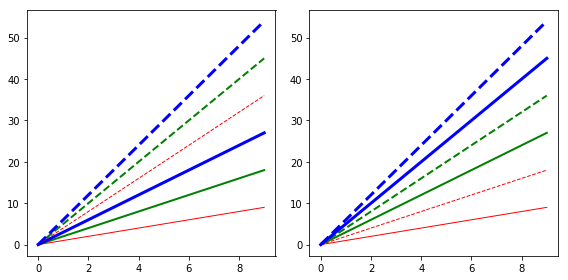
We always want to give different lines different plans
fig, ax = plt.subplots(tight_layout=True) x = np.linspace(0, 2*np.pi, 1024) for i, (lw, c) in enumerate(zip(range(4), ['r', 'g', 'b', 'k'])): ax.plot(x, np.sin(x - i * np.pi / 4), label=r'$\phi = {{{0}}} \pi / 4$'.format(i), lw=lw + 1, #lw linewidth c=c) ax.set_xlim([0, 2*np.pi]) ax.set_title(r'$y=\sin(\theta + \phi)$') ax.set_ylabel(r'[arb]') ax.set_xlabel(r'$\theta$ [rad]') ax.legend(loc=0);
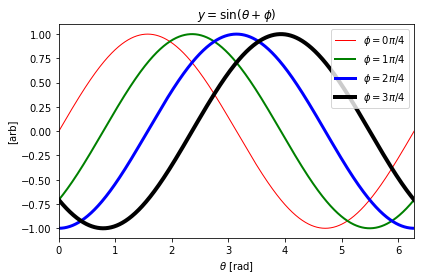
More complex
fig, ax = plt.subplots(tight_layout=True) x = np.linspace(0, 2*np.pi, 1024) for i, (lw, c) in enumerate(zip(range(4), ['r', 'g', 'b', 'k'])): if i % 2: ls = '-' else: ls = '--' ax.plot(x, np.sin(x - i * np.pi / 4), label=r'$\phi = {{{0}}} \pi / 4$'.format(i), lw=lw + 1, c=c, ls=ls) ax.set_xlim([0, 2*np.pi]) ax.set_title(r'$y=\sin(\theta + \phi)$') ax.set_ylabel(r'[arb]') ax.set_xlabel(r'$\theta$ [rad]') ax.legend(loc=0);
Course
import matplotlib.pyplot as plt import numpy as np from cycler import cycler
Our husband makes some sample data
x = np.linspace(0, 2 * np.pi, 50) offsets = np.linspace(0, 2 * np.pi, 4, endpoint=False) yy = np.transpose([np.sin(x + phi) for phi in offsets])
yy.shape
(50, 4)
Prop cycle: the property cycle, which controls some style s in future drawing
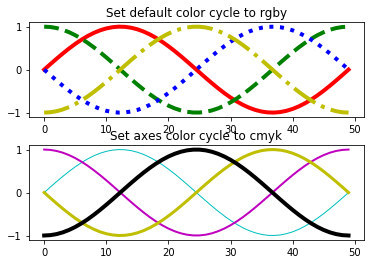
default_cycler = (cycler(color=['r', 'g', 'b', 'y']) + cycler(linestyle=['-', '--', ':', '-.'])) plt.rc('lines', linewidth=4) #Set the style of lines in the future plt.rc('axes', prop_cycle=default_cycler) #Set the style of future axes
adopt matplotlib.axes.Axes.set_prop_cycle You can set the corresponding prop cycle
custom_cycler = (cycler(color=['c', 'm', 'y', 'k']) + cycler(lw=[1, 2, 3, 4])) fig, (ax0, ax1) = plt.subplots(nrows=2) ax0.plot(yy) #default_cycler ax0.set_title('Set default color cycle to rgby') ax1.set_prop_cycle(custom_cycler) ax1.plot(yy) ax1.set_title('Set axes color cycle to cmyk') # Add a bit more space between the two plots. fig.subplots_adjust(hspace=0.3) plt.show()