Monotone queue optimization for multiple knapsack problems
Warm tips: it's better to eat dessert first and then enter the dinner~
0-1 backpack problem (dessert)
https://www.acwing.com/problem/content/2/
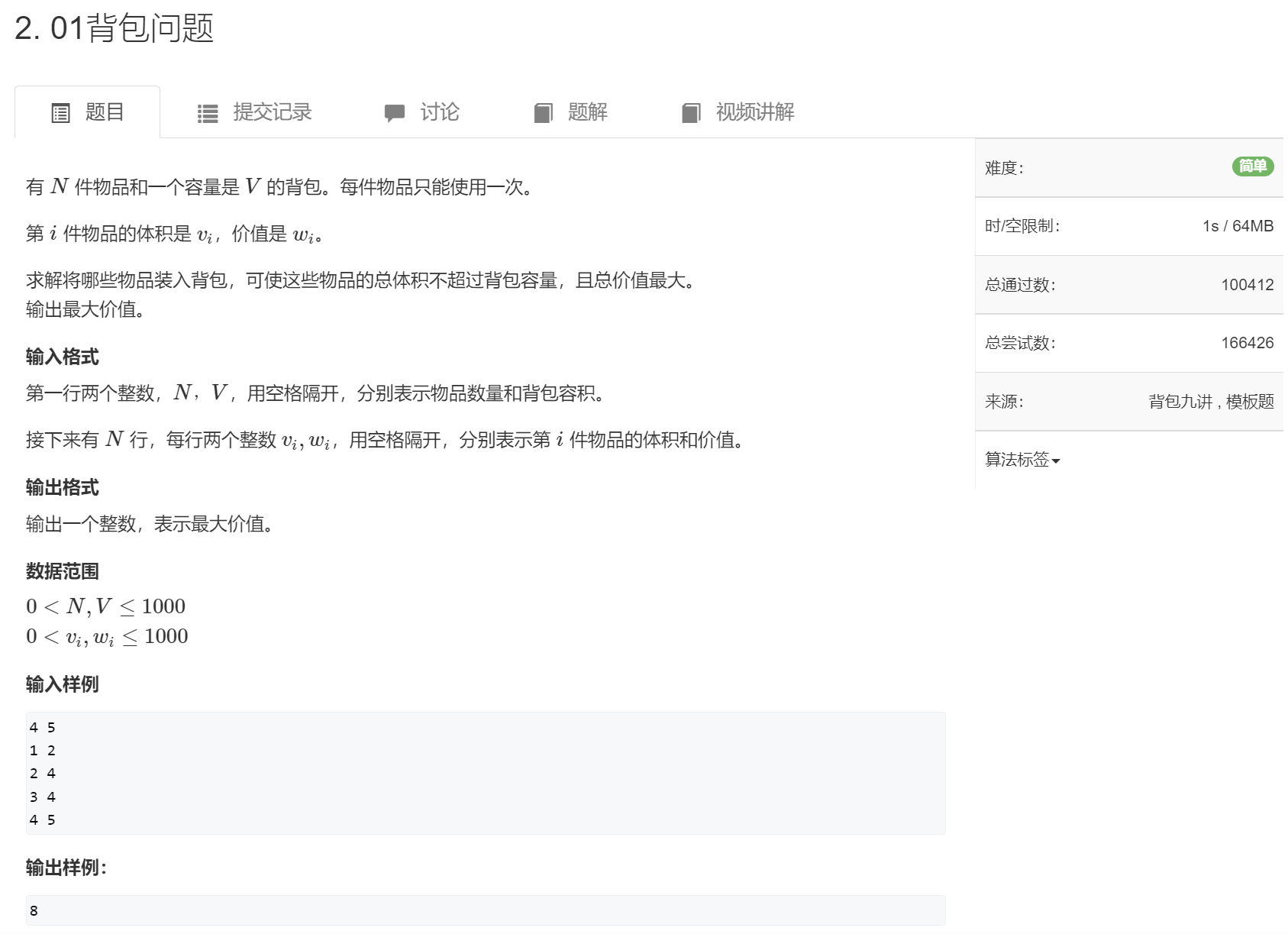
Simple solution
#include <iostream>
using namespace std;
const int N = 1010;
int n, m; //n number of items m maximum capacity of backpack
int dp[N][N]; //dp[i][j] Table: consider the maximum value of the first I items and the backpack capacity is j volume units
int v[N], w[N];
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
for (int i = 1; i <= n; i ++) {
for (int j = 0; j <= m; j ++) {
//If the ith one is not selected, dp[i][j] = dp[i - 1][j];
//Select the ith one, dp[i][j] = dp[i - 1][j - v[i]] + w[i];
dp[i][j] = dp[i - 1][j];
if (j >= v[i]) dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);
}
}
cout << dp[n][m] << endl; //Considering the first n (all) items, the maximum value of the backpack volume capacity of m is the answer
}
Spatial dimensionality reduction
The first dimension of dp is actually redundant, because I only needs the state of i-1, but in fact, at the beginning of the I-round enumeration, the second dimension of dp [i][j] represents the state of i-1, which can be reduced (as shown in the figure below).

However, we can't enumerate from small to large, otherwise the status of i will be used in subsequent status updates (as shown in the figure below).

Descending enumeration can be avoided (as shown in the figure below).

Code after dimensionality reduction and compression:
#include <iostream>
using namespace std;
const int N = 1010;
int n, m; //n number of items m maximum capacity of backpack
int dp[N]; //dp[j] Table: the backpack capacity is the maximum value of j volume units
int main() {
cin >> n >> m;
for (int i = 0; i < n; i ++) {
int v, w; //Volume and value of the ith item
cin >> v >> w;
//If the ith one is not selected, dp[j] = dp[j];
//Select the i th one, dp[j] = dp[j - v] + w;
for (int j = m; j >= v; j --) dp[j] = max(dp[j], dp[j - v] + w); //Enumeration from large to small
}
cout << dp[m] << endl;
}
Multiple knapsack problem (dinner)
https://www.acwing.com/problem/content/4/
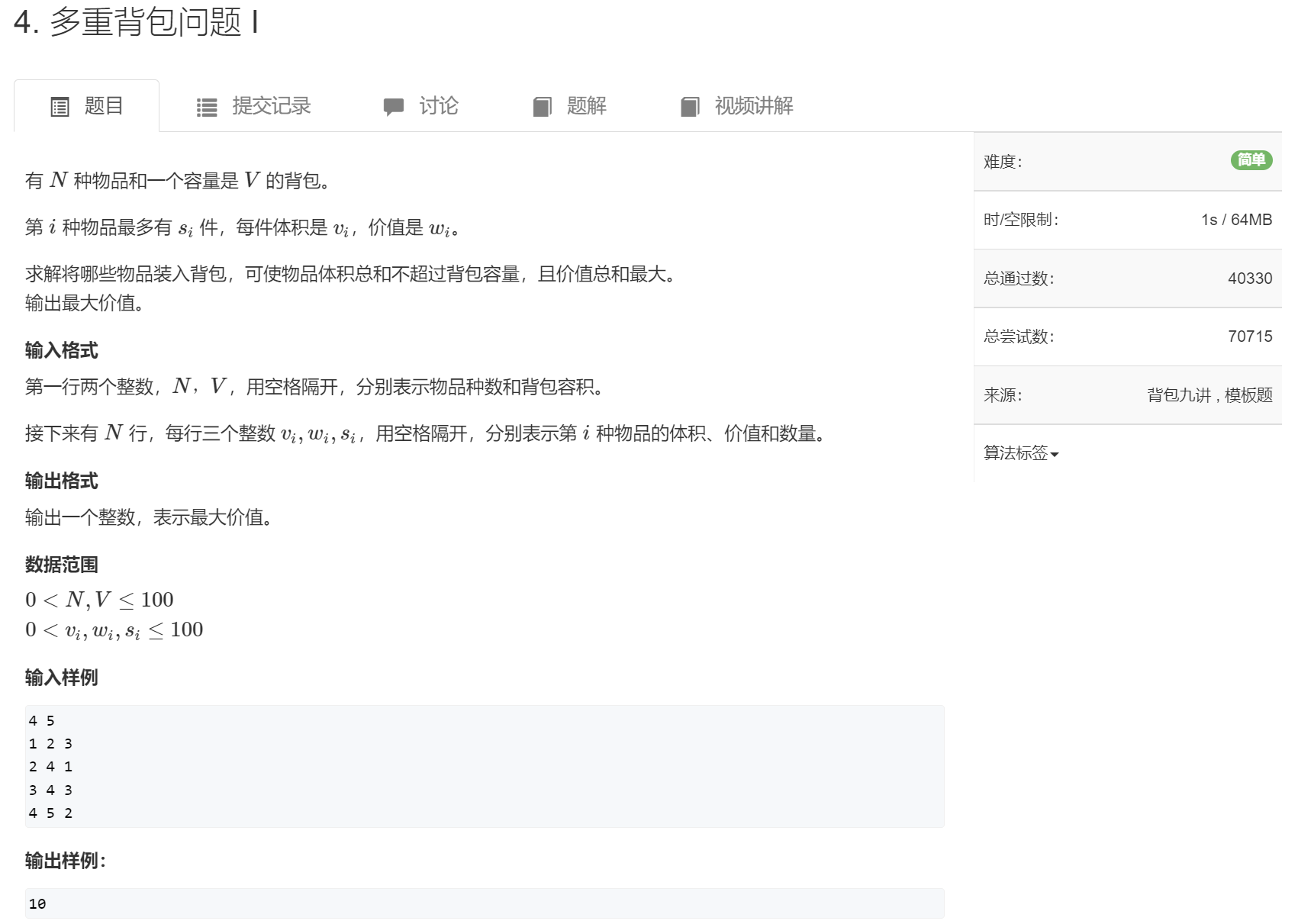
The only difference from 0-1 backpack is that multiple backpacks may have multiple items s.
The selection method is not like the 0-1 backpack: for the i-th item, choose either 0 or 1. There are only two options:
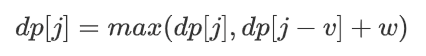
Instead, there are s+1 options [0,s]:
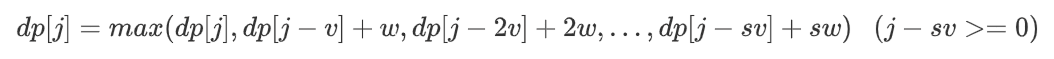
Simple (violent) solution
Add a loop to the code of 0-1 knapsack:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int n, m;
int f[N];
int main() {
cin >> n >> m;
for (int i = 0; i < n; i ++) {
int v, w, s;
cin >> v >> w >> s;
for (int j = m; j >= v; j --) {
for (int k = 1; k <= s && j >= k * v; k ++) { //Enumerate the s selection methods of [1,s] pieces and compare them with the case of not selecting
f[j] = max(f[j], f[j - k * v] + k * w);
}
}
}
cout << f[m] << endl;
}
Time complexity O(NVS) = O(N^3) complexity is very high. Consider optimizing it.
Binary optimization
https://www.acwing.com/problem/content/5/

In fact, we consider grouping each item stack (s), and regard each group as an item and solve it as a 0-1 knapsack.
In order to make the time complexity as small as possible, the number of groups we get must be as small as possible, and the random combination of these groups can continuously represent [0,s], that is, to be an equivalent class.
For example, s=7, according to the simple method above, is equivalent to being divided into seven groups: 1, 1, 1, 1, 1, 1
Here we consider binary splitting, which is divided into: 1, 2 and 4
0 = Not selected 1 = Choose 1 2 = Option 2 3 = Select 1 and 2 4 = Choose 4 5 = Select 1 and 4 6 = Select 2 and 4 7 = Select 1, 2 and 4
In fact, it is divided into:
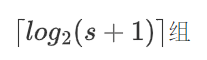
If s+1 is not a power of 2, for example, the division of 10:
Then split it into: 1 2 4 3 Where: 1 2 4 can represent[0, 7] So 1 2 4 3 can represent[0, 10]
After explaining the idea, the code:
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int dp[2010];
struct Good{
int v, w; //Volume and value of goods
};
int main(){
int n, m; //Number of items and maximum capacity of backpack
cin >> n >> m;
vector<Good> goods; //Store grouped items
for(int i = 0; i < n; i++){
int v, w, s;
cin >> v >> w >> s;
for(int j = 1; j <= s; j *= 2){ //Binary split
s -= j;
goods.push_back({v * j, w * j});
}
if(s) goods.push_back({v * s, w * s}); //Save the rest after disassembly (s here is equivalent to the remaining 3 after 10 is disassembled into 1, 2, 4)
}
for(auto good : goods){ //The item groups after equivalent split (binary split) are solved according to 0-1 knapsack method
for(int j = m; j >= good.v; j --) //Note the enumeration from large to small
dp[j] = max(dp[j], dp[j - good.v] + good.w);
}
cout << dp[m] << endl;
return 0;
}
Time complexity O(NV) × log(S))=O(N^2 × log(N)), in fact, the complexity is still not considerable.
Monotone queue optimization of extreme optimization
https://www.acwing.com/problem/content/6/

v[i] (abbreviated as v below) represents the volume of the ith item, where j=v-1 and m represents the maximum capacity of the backpack. Here we assume that m=kv+j, in fact, it may also be kv+j-1,..., kv+1,kv is just for the convenience of the following rectangular demonstration, we might as well assume that m=kv+j.
| dp[0] | dp[v] | dp[2v] | dp[3v] | ... | dp[(k-1)v] | dp[kv] |
| dp[1] | dp[v+1] | dp[2v+1] | dp[3v+1] | ... | dp[(k-1)v+1] | dp[kv+1] |
| dp[2] | dp[v+2] | dp[2v+2] | dp[3v+2] | ... | dp[(k-1)v+2] | dp[kv+2] |
| dp[3] | dp[v+3] | dp[2v+3] | dp[3v+3] | ... | dp[(k-1)v+3] | dp[kv+3] |
| ... | ... | ... | ... | ... | ... | ... |
| dp[j-1] | dp[v+j-1] | dp[2v+j-1] | dp[3v+j-1] | ... | dp[(k-1)v+j-1] | dp[(kv+j-1)] |
| dp[j] | dp[v+j] | dp[2v+j] | dp[3v+j] | ... | dp[(k-1)v+j] | dp[kv+j] |
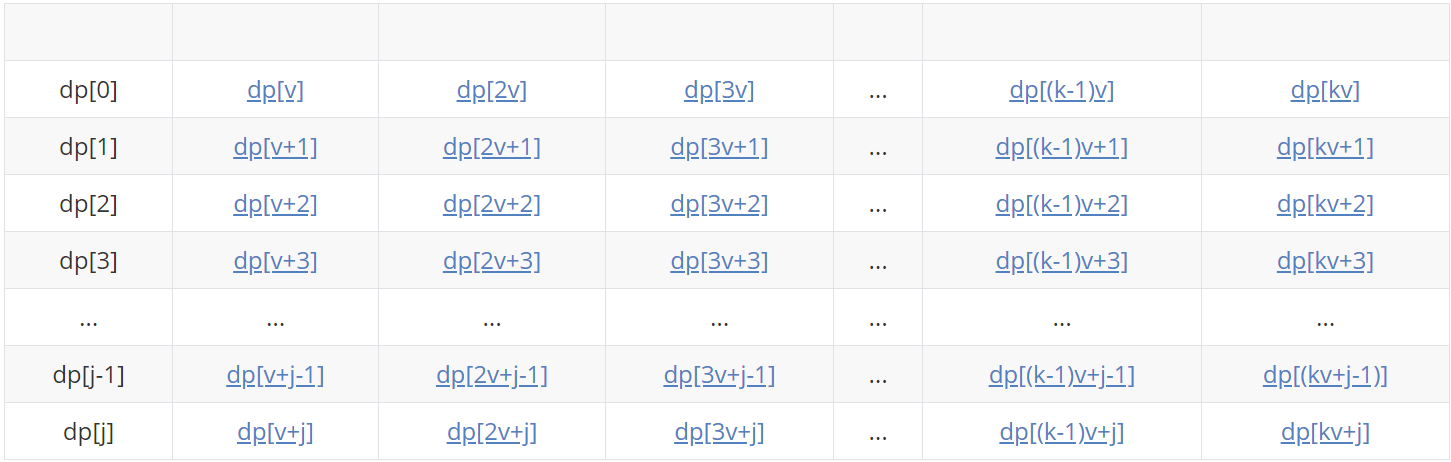
Recalling the solution mentioned above, the dp of the second layer loop implemented in the code is the state transition process: for each item i, the enumeration value will be updated from large to small in all cases of [v,m] (elements marked in blue). The enumeration sequence is shown as follows:
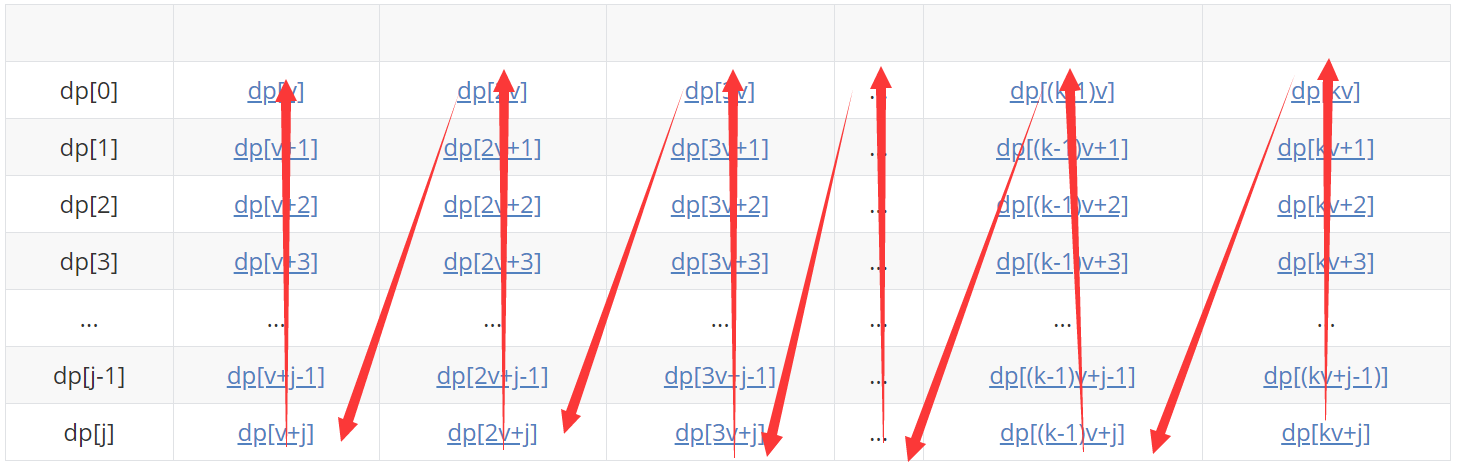
The following is a specific analysis:
The blue element represents the status to be updated (max is required), and the bold element represents the status that can be transferred to the status to be updated (of course, due to the limitation of the number of items, there may not be k, which will not be so long. Here is just for the convenience of demonstration, and the number of items will not be considered temporarily)

dp[kv+j]=max( dp[(k-1)v+j] + w , dp[(k-2)v+j] + 2w , ... , dp[3v+j] + (k-3)w , dp[2v+j] + (k-2)w , dp[v+j] + (k-1)w , dp[j] + kw )

...
...
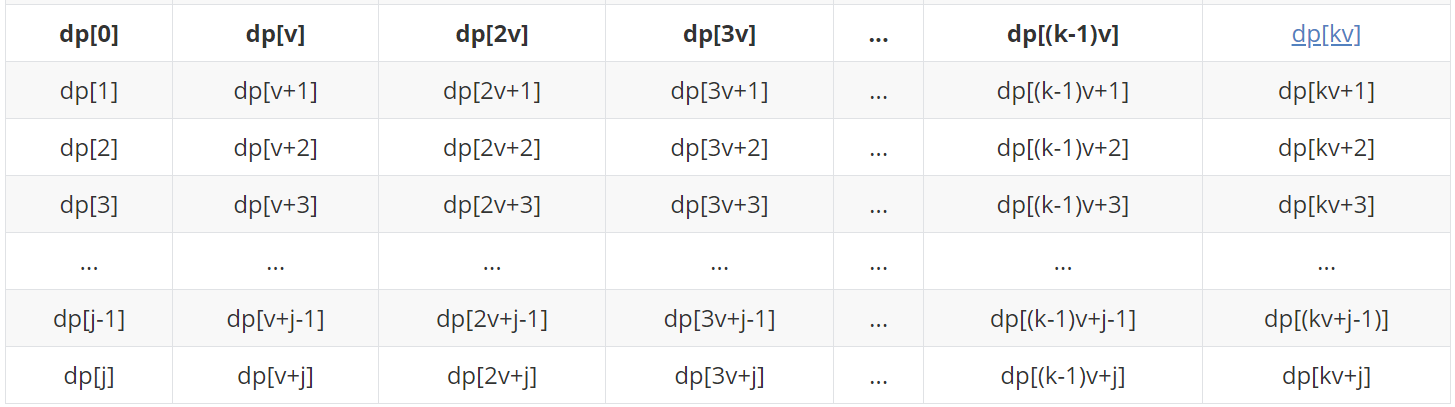

dp[(k-1)v+j]=max( dp[(k-2)v+j] + w , ... , dp[3v+j] + (k-4)w , dp[2v+j] + (k-3)w , dp[v+j] + (k-2)w , dp[j] + (k-1)w )
When you come here, compare the above figure with the following figure. Carefully, you suddenly find that there seem to be a lot of unnecessary (seemingly redundant but have to do) comparisons here. Here's the analysis:
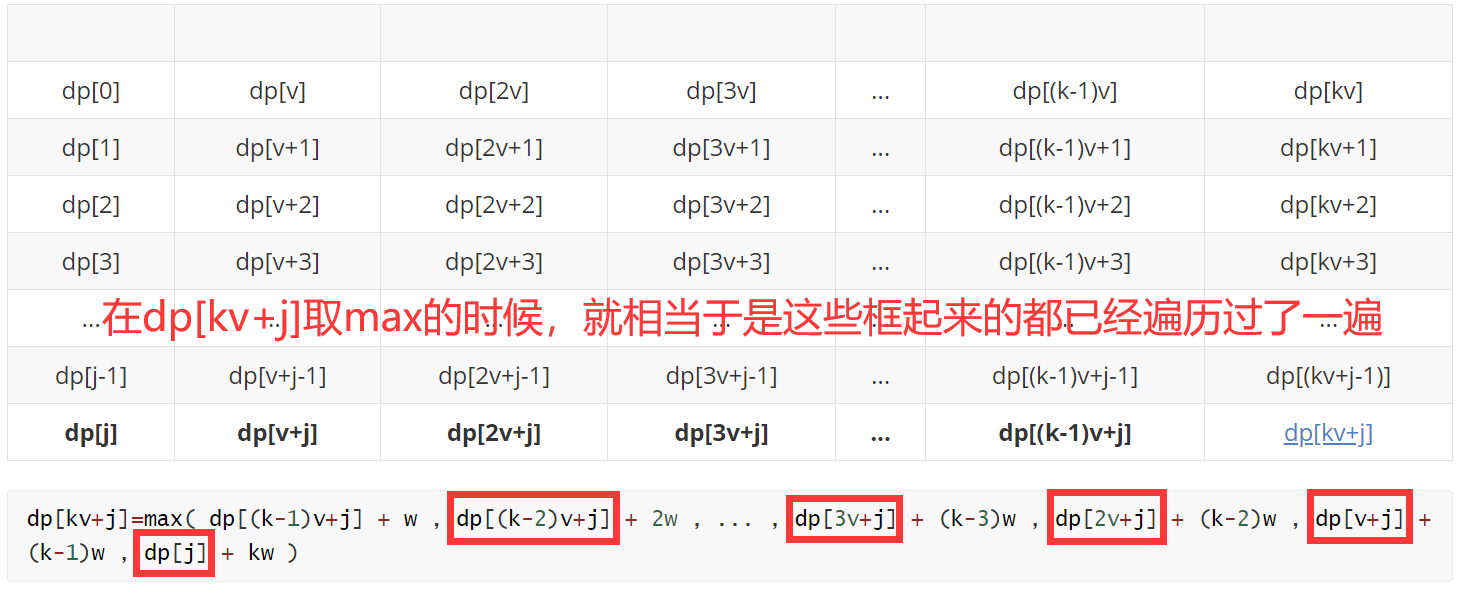
When we update the status of dp[(k-1)v+j] (take max), we traverse them again.
The problem is: each time we take max, we need to compare all elements in the set (the same row) from "0", not on the basis of the previous comparison results.
Cause of the problem: we enumerate from large to small. For example: This is equivalent to that we traverse a set of positive integers to get the maximum value of this set, and then we remove an element from the set. The maximum value of the new set is not certain for us (fine products). We can't use the work done in the last traversal (the labor results can't be used this time).
Thinking: if we do reverse thinking, we traverse a set of positive integers to get the maximum value of this set, and then we add an element to the set. The maximum value of the new set is certain for us. We can use the work done in the last traversal (the labor results can be used this time).
Solution: therefore, we should abandon the idea of "enumerating and compressing space from large to small" described above, choose enumerating from small to large, and use a data structure to simulate this "larger set", and make some restrictions on this basis to limit the number of items. Since the state can be transferred only when the difference is V, we can make an equivalent division of the whole set with the remainder of module V as the division rule, which can be divided into v subsets (module V remainder [0, v-1] represents a subset per row, which is also the purpose of designing this rectangle in this paper), At this time, we will enumerate and update each set from small to large (status update, from left to right in the following table), and also consider the number of items.
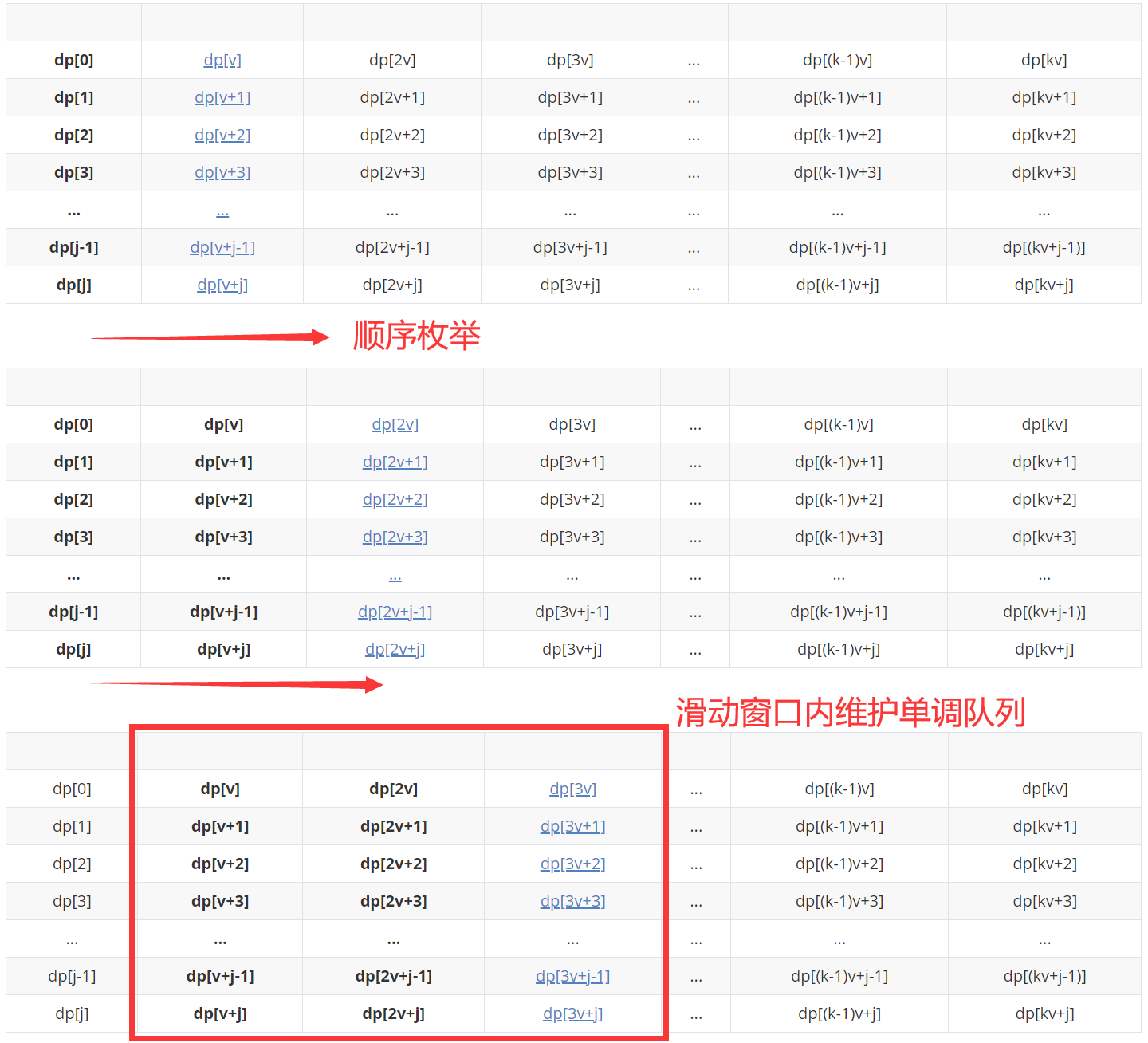
Specific implementation: take a row (a subset of congruence) as an example, set a sliding window, set the window size to the number of items + 1, and maintain a monotonic queue inside the window.
As for why the window size is the number of items + 1, for example: if there are only 2 items and dp[3v+j] is transferred from dp[j], three items need to be installed, so it is impossible to transfer from dp[j]. Therefore, it is not necessary to take dp[j] into account, just maintain a monotonous queue within the window size of 3.

First, explain the monotone queue:
As the name suggests, the focus of monotonic queue is divided into "monotonous" and "queue" "monotonous" Refers to the of an element "law"-Increasing (or decreasing) "queue" This means that the element can only be operated from the head and tail of the queue, but this"queue" Not that queue.
If the maximum value of each consecutive k number is required, it is obvious that when a number enters the range of the maximum value to be "looked for", if this number is larger than the number in front (the first team), it is obvious that the number in front will be out of the team first and can no longer be the maximum value.
In other words - when the above conditions are met, the number in front can be "kicked out" and then push ed into the end of the team.
This is equivalent to maintaining a decreasing queue, which conforms to the definition of monotonous queue and reduces the number of repeated comparisons (the previous "labor achievements" can be used later). Moreover, since the maintained team is within the query range and decreasing, the team head must be the maximum value in the query area, so only the team head needs to be output when outputting. It is obvious that in such an algorithm, each number only enters and exits the team once, so the time complexity is reduced to O(N).
If you don't understand the text interpretation, it doesn't matter. Let's introduce it in combination with simulation: assuming that the number of items is 2, the window size is 3, and the simulation is carried out. In this process, because we update from small to large, we need to back up a copy of the i-1 state of dp to g (space for time).
First, put g[j] at the end of the queue. At this time, there is only g[j] in the monotonic queue. Update dp[j] with queue head g[j]:

dp[j] becomes the state when i is updated. Here we assume (G [J] + W > G [V + J]).
g[v+j] before joining the team, start at the end of the team and kick out all those not bigger than it, and then enter the end of the team (g[j]+w is bigger than it and can't be kicked out).
Take team leader g[j]+w update dp[v+j]:
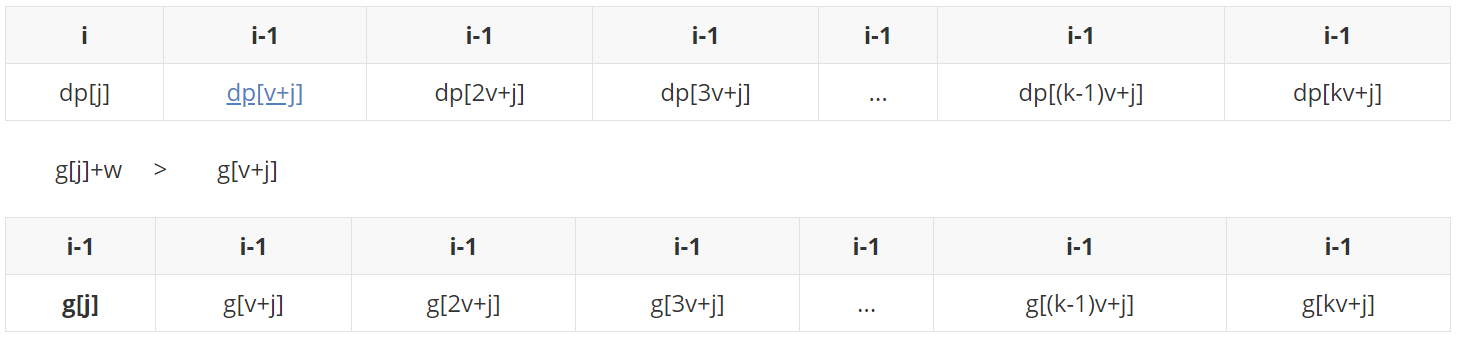
The state when dp[v+j] changes to i after updating.
(case 1) if (G [J] + 2W > G [V + J] + W > G [2V + J]).
g[2v+j] before joining the team, compare it from the end of the team. It is found that the end of the team is bigger than it and can't play. Then join the end of the team obediently.
At this time, take the team head g[j]+2w to update dp[2v+j]:
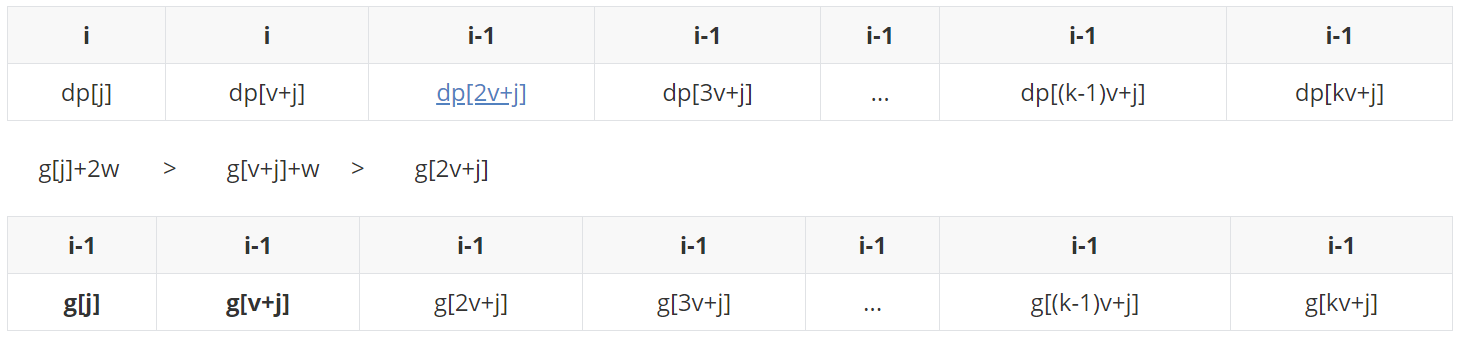
(case 2) if (G [J] + 2W > G [2V + J] > = g [V + J] + W).
Before g[2v+j] joined the team, he found that the g[v+j]+w at the end of the team was not bigger than it, and kicked it out. Then he compared the g[j]+2w at the end of the team, which was bigger than it, and joined the end of the team obediently.
At this time, take the team head g[j]+2w to update dp[2v+j]:

(case 3) if (G [2V + J] > = g [J] + 2W > G [V + J] + W).
Before g[2v+j] joined the team, he found that the g[v+j]+w at the end of the team was not bigger than it and kicked it out. Then he compared the g[j]+2w at the end of the team, which was not bigger than it and kicked it out. At this time, the queue is empty and it enters the queue.
At this time, take the team head g[2v+j] to update dp[2v+j]:
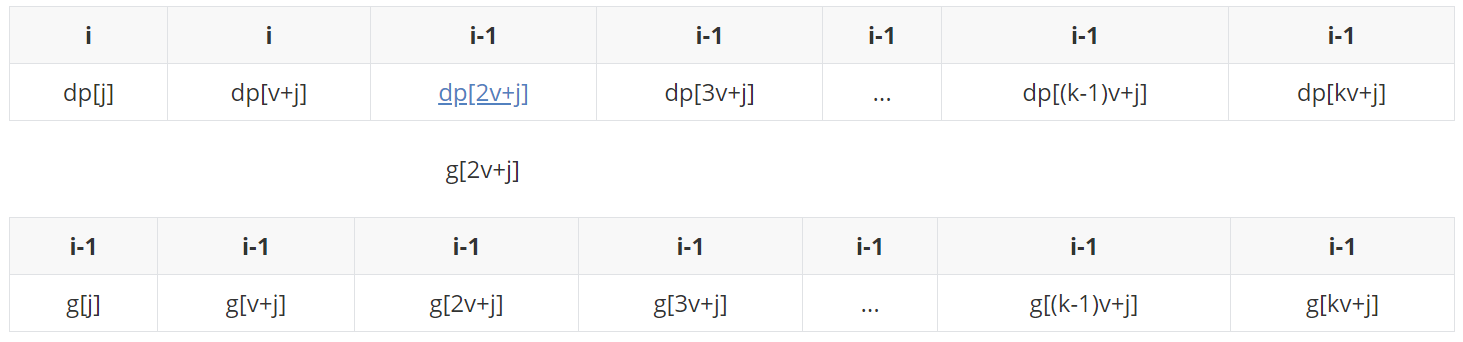
Suppose we end with the first of the above three cases (G [J] + 2W > G [V + J] + W > G [2V + J]):

The state when dp[2v+j] changes to i after updating.
Before g[2v+j] joins the team, check whether all the elements in the monotonic queue are within the window (length is 3). If g[j]+3w is not found, kick it out, and then
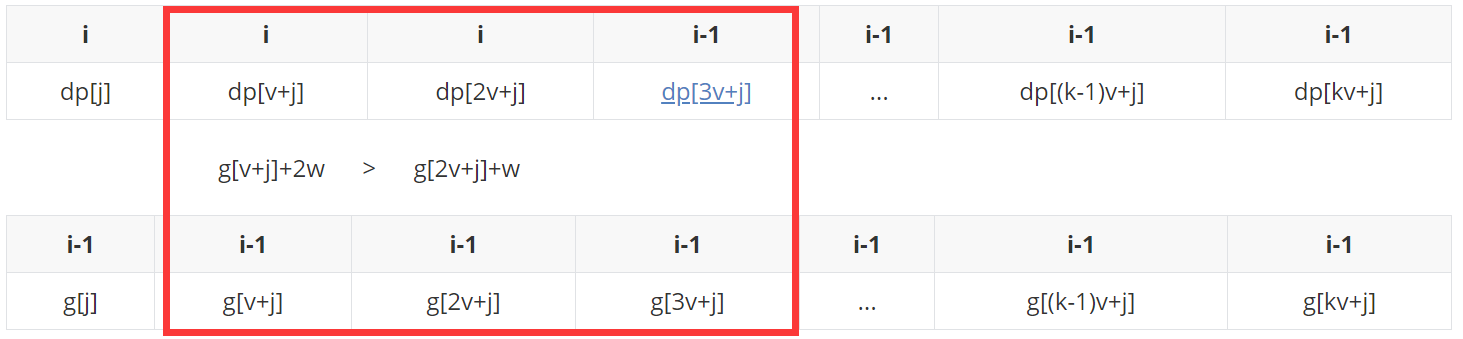
So far, the rules and ideas of monotone queue maintenance in this problem have been demonstrated clearly. The following code is directly shown:
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
//Multiple knapsack problem: limit the number of times each item can be taken
//Extreme Optimization: monotone queue
const int M = 20010, N = 1010;
int n, m;
int dp[M], g[M];
int que[M]; //The queue is only stored in the congruence set, and the corresponding value is not stored
int main() {
cin >> n >> m;
for(int i = 0; i < n; i ++){
int v, w, s;
cin >> v >> w >> s;
//Copy a copy g, because it will grow from small to large, not from large to small like 0-1 backpack, so you must apply for the copy to be saved in i-1 status, otherwise it will be affected
memcpy(g, dp, sizeof dp);
for(int r = 0; r < v; r ++) { //Because only the states of congruence with V can affect each other, congruence 0,1, V-1 is divided into group v
int head = 0, tail = -1;
for(int k = 0; r + k * v <= m; k ++) { //Processing each group is equivalent to processing all States
//Kick out when the team leader is not in the window (the dp of the team leader distance to be updated exceeds the maximum number s, although it should be rounded off no matter how large, because it can't be reached)
if(head <= tail && k - que[head] > s) head++;
//The k-th one is ready to come in and kick out all the tail of the team no larger than it, also in order to maintain the monotony of the queue (the judgment formula is actually subtracting k * w from both sides at the same time)
//The actual meaning should be that G [R + k * V] > = g [R + que [tail] * V] + (k - que [tail]) * W is the judgment condition
while(head <= tail && g[r + k * v] - k * w >= g[r + que[tail] * v] - que[tail] * w) tail --;
que[++ tail] = k; //List the k-th item in the column. The queue is only stored in the congruence. The corresponding value is not stored
//The k-th group of Yu r takes the team head to update, and the team head is always the decision to make it max
dp[r + k * v] = g[r + que[head] * v] + (k - que[head]) * w;
}
}
}
cout << dp[m] << endl;
return 0;
}
Time complexity:
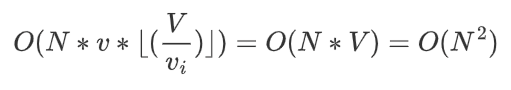
Please correct any mistakes in the above contents.