Directory QWQ
Monotone stack and monotone queue
abstract
Monotone queues and monotone stacks require monotone elements on the basis of ordinary queues and stacks. In fact, the application of monotone queues and monotone stacks is also based on their monotonicity.
In fact, I don't think the difference between these two special data structures is too large (at least from the following examples). Suppose we all use deque's push_back() to add new elements, because to meet the monotonicity, there must be a pop compared with back ()_ Operation of back(). Normally, this is a stack operation (FIFO), which is not allowed in the queue. Traditional queues only allow pop_front(). Therefore, it is found that monotonic queues also need stack like operations.
So when are monotone queues and monotone stacks used? In fact, for monotonous queues, it is precisely because it allows pop_front() operation, so if there is a limit on a length and then a maximum / minimum value is required, it should be a monotonic queue. If there is a feeling of seeking "nearest", it should be monotonous stack.
- deque's common functions are front(), back(), and push()_ front(), push_ back(), pop_ front(), pop_ back(), size(), empty()…
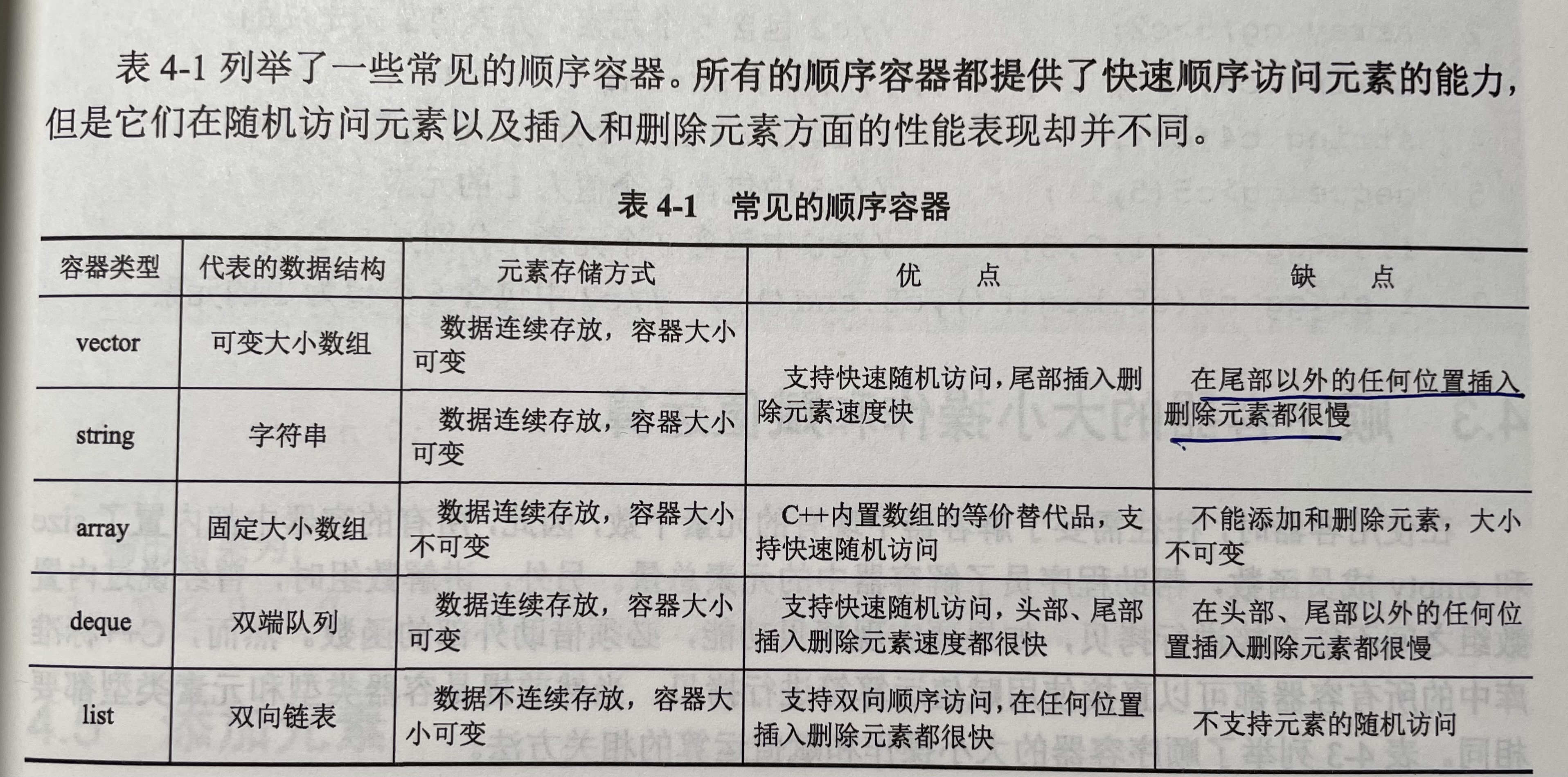
Comparison of common sequential containers:
Monotone stack
-
Monotone stack: as the name suggests, the elements in this stack remain monotonic (monotonic increasing or monotonic decreasing)
Using monotonicity, it is convenient to take the first element larger / smaller than him on the left of the current element (that is, the nearest element larger / smaller than him adjacent to the current element)
-
Idea of maintaining monotone stack: compare the current element with the stack top element. If the stack top element is larger than the current element, the stack top element will be out of the stack; Repeat processing until the stack is empty or the top element is smaller than the current element (monotonically increasing the stack)
E x a m p l e − 1 Example -1 Example − 1 query
| Title Description | For a sequence of n positive numbers, ask the first number to the left of each number that is smaller than it. If not, output - 1. |
|---|---|
| sample input | 6 1 2 3 4 5 6 |
| sample output | -1 1 2 2 3 4 |
-
Problem analysis:
Find the nearest number on the left that is smaller than the current element, a typical application of monotone stack.
-
code:
(this question is a question on the PPT, so the code is a general idea of the monotonous stack, and the preciseness is not guaranteed!)
#include <bits/stdc++.h>
using namespace std;
int num[100];
deque<int> de;//Monotone stack
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; i++)
scanf("%d", &num[i]);
for (int i = 1; i <= n; i++) {
//Compare the top element of the stack with the current element to ensure the monotonicity of the stack after adding the current element
//(if the stack is not empty) take the top element of the stack, which is the nearest value to the current element that is smaller than the current element
//Stack the current element
while(!de.empty()&&num[de.back()]>num[i])
de.pop_back();
if(de.empty()) printf("-1");
else printf("%d", num[de.back()]);
de.push_back(i);
if(i!=n) printf(" ");
}//for
}
E x a m p l e − 2 Example -2 Example − 2 happiness index
| Title Description | What is the happiest time in life? Happiness index may help you find out. Happiness index requirements: give a happiness value to your daily life. The greater the happiness value, the happier it is. The happiness index for a period of time is the sum of the happiness value for this period of time multiplied by the minimum value of the happiness value for this period of time. The period with the greatest happiness index may be the happiest time in life. |
|---|---|
| Input format | In line 1, an integer n, 1 ≤ n ≤ 100000, indicates the number of days to be investigated. Line 2, n integers H i H_i Hi, separated by spaces, H i H_i Hi = happiness value on day i, 0 ≤ H i ≤ 1000000 0≤H_i≤1000000 0≤Hi≤1000000. |
| Output format | The first line, an integer, represents the maximum happiness index. In line 2, two integers l and r, separated by spaces, represent the interval corresponding to the maximum happiness index [ l , r ] [l,r] [l,r]. If there are multiple such intervals, the longest and leftmost interval is output. |
| sample input | 7 6 4 5 1 4 5 6 |
| sample output | 60 1 3 |
| limit | Time limit: 100 ms Memory limit: 64 MB |
(Ps: as like as two peas of last semester's data structure, it's impossible to find OJ exactly the same.
-
Problem analysis:
How to seek happiness? It's natural to think, first determine the interval [ l , r ] [l,r] [l,r], then find the minimum value in the interval and find the happiness value. This idea is pure violence, no skills, time complexity O ( n 2 ) O(n^2) O(n2) .
We might as well change our thinking: first determine a number a i a_i ai, then find the interval [ l i , r i ] [l_i,r_i] [li, ri], let a i a_i ai becomes the minimum value in this interval. How to base a i a_i ai , find the interval [ l i , r i ] [l_i,r_i] What about [li, ri]?
We are a i a_i ai , find a number on the left l i ′ l_i' He is with a i a_i ai = nearest $< A_ I $; Again in a i a_i ai , find a number on the right r i ′ r_i' ri ', also with $a_i $nearest $a_i $. It can be concluded that, l i ′ l_i' li 'to $r_i '$this interval (excluding l i ′ , r i ′ l_i',r_i' In the number of li ′, ri ′, $a_i $is the smallest. There should be a simple proof here, but it seems to understand, so it's omitted.
So, l i , r i l_i,r_i li and ri are respectively l i ′ l_i' The number after li 'and $R_ S the previous number, so we can roughly determine the interval. But there are some details to consider carefully:
-
First of all, pay attention to this l i ′ l_i' li ′ and $r_i '$is $< A_ I $or $\ leq a_i $, because there may be consecutive repeated numbers.
For example... 0 6 6... Here are 5 6, if you want to judge the left section of the third 6, if yes ≤ \leq ≤, the left interval is the second 6; If it is < < < the left section is the first 6. We want the interval to be longer, so the interval sum will be larger, so it is $< a_ i$.
During programming, it will be reflected in judging while (! De.empty() & & num [de.back()] > = num [i]) when maintaining monotone stack. You can't > judge here! Of course, you can also try both the greater than sign and greater than or equal to, and you'll know it's right.
-
Also consider if a i a_i If there is no smaller element on the left side of ai , then he himself is the boundary on the left. For the boundary processing method, you can directly use if/else, or skillfully handle the num value of the edge (num[0] and num[n+1]). You can refer to the second code.
Seeking the nearest value smaller than the current element is monotonically increasing the stack! So you can consider writing code. Normally, the time complexity of a monotone stack is O ( n ) O(n) O(n).
-
-
Problems needing attention:
- When comparing the current element with the top element of the stack, you should use > = instead of >
- Read the question carefully and pay attention to the sentence "if there are multiple such intervals, output the longest and leftmost interval". It takes up a whole 40 40 40 points! The interval length should be considered carefully, α \alpha α reach β \beta β The interval length is β − α + 1 \beta-\alpha+1 β − α+ 1. Consider specific issues (see notes for details)
-
My code:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MaxN = 1e5+5;
const int inf = 0x3f3f3f3f;
deque<ll> de;
ll num[MaxN], sum[MaxN], qian[MaxN], hou[MaxN];
//num is used to store numbers. sum[i] is the prefix and sum of the first I numbers
//qian/hou are the intervals on both sides of the i-th element, which are obtained through the monotone stack
//You can directly save the subscript of the nearest element smaller than the current element in these two arrays
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; i++) {
scanf("%lld", &num[i]);
sum[i] = sum[i-1]+num[i];
}
//Monotone stack
for (int i = 1; i <= n; i++) {
//Just do it again
while (!de.empty() && num[de.back()]>=num[i])
de.pop_back();
//(when the stack is not empty) at this time, the element at the top of the stack is the nearest value (subscript) smaller than the current element
if (de.empty()) qian[i] = 1;
else qian[i] = de.back()+1;//The situation is discussed
de.push_back(i);
}
while (!de.empty()) de.pop_back();
for (int i = n; i >= 1; i--) {//Error 1 is written here as i++
//Do it the other way around
while (!de.empty() && num[de.back()]>=num[i])
de.pop_back();
if (de.empty()) hou[i] = n;
else hou[i] = de.back()-1;
de.push_back(i);
}
//output
ll f,r,res=-inf;
for (int i = 1; i <= n; i++) {
ll a = qian[i]-1;
ll b = hou[i];
ll c = (sum[b]-sum[a])*num[i];
if (res<c) res=c,f=a+1,r=b;
else if (res==c && (b-a)>(r-f+1)) f=a+1,r=b;
//It's a big pit here... I forgot to consider 60 points at first, then compared it with (b-a) and (r-f), and then 80 points
//But in fact, the number of elements in the interval x to y should be y-x+1
//Because b-a already contains a 1 (in fact, the calculation interval sum needs to make a=qian[i]-1), so + 1 is not used here
//But r-f needs to add 1!
//Of course, if you directly compare hou[i]-qian[i] and r-f, you may not consider it so detailed
//This tells us not to set so many letters blindly
}
cout << res << endl << f << " " << r;
}
- Another big man's code:
#include <bits/stdc++.h>
using namespace std;
const int INF = 1e9;
const int mod = 1e9 + 7;
const int maxn = 1e5 + 5;
typedef long long ll;
ll sum[maxn];
int h[maxn],l[maxn],r[maxn];
int n;
ll ma, posl, posr;
stack<int> q;
int main() {
scanf("%d", &n);
h[0] = h[n+1] = -INF;
for (int i = 1; i <= n; ++i) {
scanf("%d", &h[i]);
sum[i] = sum[i-1] + h[i];
}
q.push(0);
for (int i = 1; i <= n; ++i) {
while (!q.empty() && h[q.top()] >= h[i]) q.pop();
l[i] = q.top();
q.push(i);
}
while (!q.empty()) q.pop();
q.push(n+1);
for (int i = n; i >= 1; --i) {
while (!q.empty() && h[q.top()] >= h[i]) q.pop();
r[i] = q.top();
q.push(i);
}
ll tmp = 0; ma=0;
for (int i = 1; i <= n; ++i) {
tmp = (sum[r[i]-1] - sum[l[i]])*h[i];
if (tmp > ma) {
ma = tmp;
posl = l[i]+1;
posr = r[i]-1;
}
else if (tmp == ma) {
if (posr-posl < r[i]-1-l[i]-1) {
ma = tmp;
posl = l[i]+1;
posr = r[i]-1;
}
}
}//for
printf("%lld\n%lld %lld\n", ma, posl, posr);
}
Monotone queue
-
Monotone queue: a special queue in which the elements keep monotonically increasing or decreasing
Using monotonicity, the first element of a monotonic queue is the maximum / extreme value of a continuous number (for example, the first element of a monotonically increasing queue is the minimum)
-
Maintenance of monotonic queue:
Monotonicity maintenance: compare the current element with the tail element. If the tail element is larger than the current element, the tail element will be out of the queue; repeat the processing until the queue is empty or the tail element is smaller than the current element; the current element will be in the queue. (monotonically increasing queue)
Interval maintenance: if the position of the first element of the team is not in the interval, the first element of the team will be out of the team; repeat the processing until the first element of the team is in the interval
-
(monotone queues have other applications, such as optimal dynamic programming)
E x a m p l e − 1 Example -1 Example − 1 minimum value in interval m
| Title Description | The number sequence of n numbers outputs the minimum value in each interval of length m from left to right |
|---|---|
| sample input | 6 3 1 2 5 3 4 6 |
| sample output | 1 2 3 3 |
-
Idea:
A typical application of monotone queue requiring the minimum value in a given interval.
-
code:
(this question is on the PPT, so the code is a general idea of monotonous queue, and the preciseness is not guaranteed!)
#include <bits/stdc++.h>
using namespace std;
int n,m;
int num[100];
deque<int> de;
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
scanf("%d",&num[i]);
//The current element is compared with the element at the end of the queue to ensure monotonicity
//Join the current element
//Delete the team head element outside the interval and maintain the interval
while(!de.empty() && num[de.back()]>=num[i])
de.pop_back();
de.push_back(i);
if(i<m) continue;
while(i-de.front() >= m) de.pop_front();//Subscript variance maintenance interval
printf("%d",num[de.front()]);
if(i!=n) printf(" ");
}
}
E x a m p l e − 2 Example -2 Example − 2 favorite sequence
| Title Description | Xiao Tang has been studying sequences for a while. He takes a sequence of N integers and assigns a favorite value to each integer in the sequence. The favorite value is also an integer, positive and negative. The larger it is, the more he likes. He wants to know how to continuously take up to m numbers from the sequence, and he obtains the maximum favorite value. 1 ≤ n ≤ 500000, 1 ≤ m ≤ n. |
|---|---|
| Input format | The first line is two integers n and M. they represent the number of numbers in the sequence and the maximum number that can be taken. The second line is N integers separated by spaces. The ith integer Li represents his favorite value for the ith number. │ Li │≤ 1000 |
| Output format | One line and three numbers represent the maximum favorite value and the first interval to take the maximum favorite value. |
| sample input | 5 2 1 4 5 2 3 |
| sample output | 9 2 3 |
| limit | Time limit: 400 ms Memory limit: 64 MB |
(Ps: it is also a topic of data structure computer experiment)
-
Title Meaning:
Find the maximum value of a continuous number sum in the sequence, which limits the length of the sequence to no more than m.
(if the sequence length is not limited, it should be another solution. It is said to be DP. Topic link: P1115 maximum sub segment and - Luogu)
-
Idea:
The problem is well understood. It must be what skills should be used to solve this problem.
First, you can use prefix and optimize the sum of consecutive numbers. The sum from A to B (including A and b) is s u m [ A ] − s u m [ B − 1 ] sum[A]-sum[B-1] sum[A] − sum[B − 1] (note here B − 1 B-1 B − 1), which is easy to think of.
The next step is how to solve it. We can let I traverse from 1 to n, take the i-th number as the end of a continuous number, and then find the j-th number( j ≤ i j\leq i j ≤ i), so that the sum of the numbers from j to i is the largest.
It is simpler to use sum array to express the above statement: given sum[i], find a j to make sum[i]-sum[j-1] maximum. Because the value of sum[i] can be understood as a fixed value, if you want to know J, you must ensure that sum[j-1] and sum[i] differ the most. Because the range m is limited in the topic, sum[j-1] In this way, we transform the problem into the minimum value problem in m in the interval of sum array solved by monotone queue.
-
code:
#include <bits/stdc++.h> using namespace std; typedef long long ll; const int inf = 0x3f3f3f3f; const int MaxN = 5e5+5; ll sum[MaxN]; int n,m,f,r; deque<ll> de; int main() { cin >> n >> m; for (int i = 1; i <= n; i++) { scanf("%lld",&sum[i]); sum[i] += sum[i-1]; } ll res = -inf; for (int i = 1; i <= n; i++) {//Monotone queue part while (!de.empty() && sum[de.back()]>sum[i])//Maintain monotonicity de.pop_back(); de.push_back(i); while (de.back()-de.front() >= m)//Maintenance interval de.pop_front(); if (sum[de.back()]-sum[de.front()-1] > res || (sum[de.back()]-sum[de.front()-1]==res)&&(de.front()<f)) { res = sum[de.back()]-sum[de.front()-1]; f = de.front(); r = de.back(); }//The de.back() in lines 20, 22, 23, 24 and 26 can be replaced by i } cout << res << " " << f << " " << r; } -
Extension:
Simple two-dimensional prefix and (I named it myself, but it seems to have it). I met it in the second question of water CSP. The question is: 202104-2 neighborhood mean.
This problem is to repeat the addition operation on the two-dimensional matrix. If it is written violently, it can only score 70 points, so it should be optimized in the summation place.
My own method is to define a two-dimensional prefix and. The details are as follows:
s u m [ m ] [ n ] sum[m][n] sum[m][n] represents the sum of the elements of the matrix of the first m rows and N columns.
Calculation method when entering: s u m [ i ] [ j ] = s u m [ i − 1 ] [ j ] + s u m [ i ] [ j − 1 ] − s u m [ i − 1 ] [ j − 1 ] sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1] sum[i][j]=sum[i−1][j]+sum[i][j−1]−sum[i−1][j−1]
(it's about adding the sum of the two matrices and subtracting the weighted part)Calculate the upper left coordinate as ( a , b ) (a,b) (a,b), the coordinates of the lower right corner are ( c , d ) (c,d) Sum of matrices of (c,d): s u m [ c ] [ d ] − s u m [ a − 1 ] [ d ] − s u m [ c ] [ b − 1 ] + s u m [ a − 1 ] [ b − 1 ] sum[c][d]-sum[a-1][d]-sum[c][b-1]+sum[a-1][b-1] sum[c][d]−sum[a−1][d]−sum[c][b−1]+sum[a−1][b−1]
(the method is the same as that of input.)Be sure to draw a diagram here to deepen your understanding (pay attention to the subscript - 1)
After this optimization, you can easily complete this problem.