MP method viscosity calculation of Lammps

This article is written by D r . X i a n \color{Violet} \rm Dr. Xian Written by Dr.Xian, mainly introduces l a m m p s \color{Violet} lammps lammps MP method for calculating viscosity. ♡ \heartsuit ♡
E m a i l : \rm \color{Violet}Email: Email: Victor_Xian285@163.com

preface

The physical quantity that measures the viscosity of a fluid is called viscosity. Generally speaking, viscosity is the measure of internal friction that hinders fluid flow. In the study of molecular dynamics, the analysis of fluid transport properties and thermal properties is inseparable from the calculation of viscosity. In some research fields (lubrication, nanofluids, etc.), the accurate calculation of system viscosity is very important. This blog first introduces the principle of MP method for calculating viscosity, and takes Ar system as an example to introduce the MP method of lammps for calculating viscosity. Compared with GK method, this method is faster and easier to analyze and deal with.

Note: the following is the main content of this article. The following case takes the calculation of viscosity of Ar system at 100K as an example for reference.

1, Calculation method and principle of viscosity MP

In short, the MP method calculates the viscosity by constructing the shear field and combining the transverse linear momentum flux. The relationship between the three can be described by the following formula, in which the momentum flux j z ( p x ) \color{red}{j_{z}(p_{x})} jz (px) is momentum p x \color{red}p_{x} The x component of px, which transports in the z direction in a given time; ∂ v x ∂ z \color{red}{ \frac{\partial v_{x}}{\partial z}} ∂ z ∂ vx ∂ is x \color{red}{x} The gradient of velocity in x direction in Z direction can be transformed to obtain the second formula below, which is l a m m p s lammps The formula used to calculate shear viscosity in lammps is more understandable.

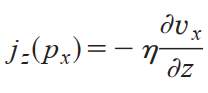
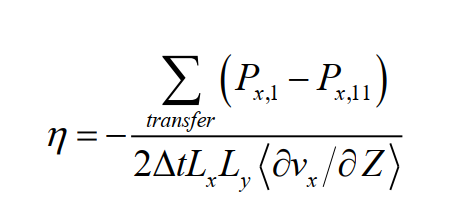
In general, for the calculation of viscosity, we need to construct a shear field in the system and count the momentum flux perpendicular to the shear direction, as shown in the figure below.

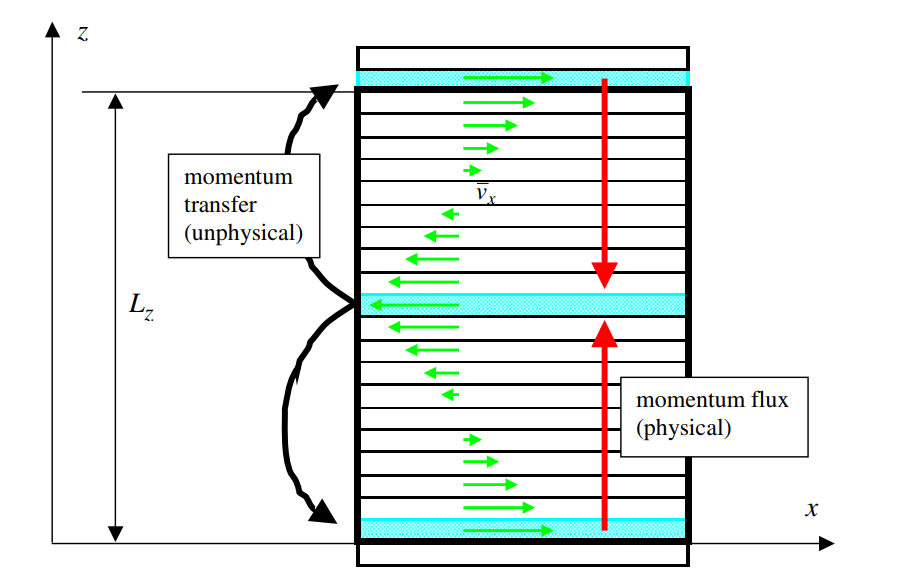
2, LAMMPS realizes the construction of shear field and counts the momentum exchange

stay M P MP In MP method, the system along z z The z direction (any coordinate direction) can be divided into 20 b i n s bins bins, by exchanging numbers 1 and 20 b i n bin bin and No. 11 b i n bin Atom in bin x x The momentum component in x direction realizes the construction of velocity gradient and then forms shear field. This momentum exchange process is non physical and artificially constructed by us. At the same time, the momentum exchange in the z direction of statistical physics is used for calculation.

Specific use f i x   v i s c o s i t y \rm fix\ viscosity The fix visibility command is used to exchange momentum and count momentum transfer in a certain direction c o m p u t e   c h u n k / a t o m \rm compute\ chunk/atom Use the compute chunk/atom command to realize region division f i x   a v e / c h u n k \rm fix\ ave/chunk The fix save / chunk command will x x The velocity and momentum exchange in the x direction are output for viscosity calculation. The command uses the following:

fix MP_v all viscosity 10 x z 20                                          #The momentum in the x direction is exchanged every 10 steps, and the momentum transfer direction is the z direction
compute layers_eta all chunk/atom bin/1d z center 0.05 units reduced      #It's divided into 20 pieces in the z direction
fix ave_vx all ave/chunk 20 50 1000 layers_eta vx file MP_vx.txt          #The output is the speed in the x direction

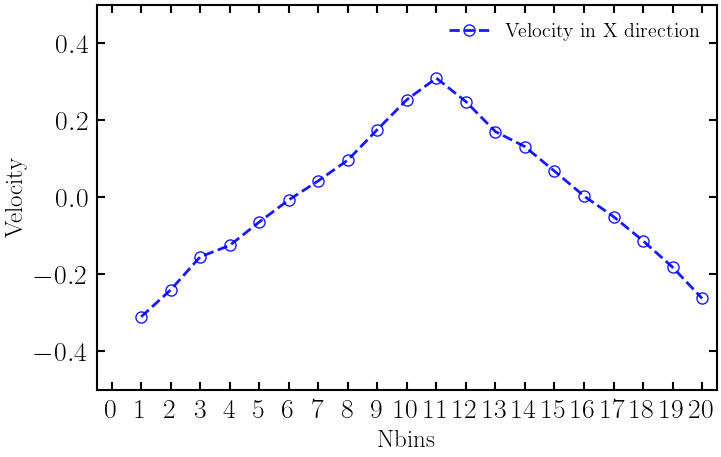
Of particular note is the momentum exchange frequency N N The choice of N has a certain influence on the calculation results of system viscosity. In practical calculation, we should choose different sizes of n N N N is calculated and compared N N Output under N x x The velocity gradient in x direction shall be selected with good linearity of velocity gradient as far as possible N N N to obtain more accurate calculation results.

3, Ar viscosity calculation case display

1.   i n writing piece as lower \color{red}{1.\ in file is as follows} 1. The documents are as follows:

# Created on Sun Jan  9 19:24:44 2022
# @author: a Lei works hard

echo              screen
units             metal
dimension           3
boundary          p p p
atom_style        full

# Define several parameters 
variable    T  equal 100                              # The temperature is 100 K
variable    A  equal 5.4                              # The lattice constant is about 5.4 A
variable    DT equal 0.01                             # The integration step is 10 fs

#Read model
read_data Ar4000.data

#Force field setting
pair_style   lj/cut 10.0                               # The cutoff radius of LJ potential is 10 A
pair_coeff   * * 1.032e-2 3.405                        # epsilon and sigma
velocity     all create ${T} 12345                     
timestep     ${DT}                                     
thermo          1000
thermo_style	custom step temp pe ke etotal density

#Simple relaxation
fix 1 all npt temp 100 100 1 iso 1 1 10
run 50000

#Viscosity calculation
reset_timestep  0
variable    dt equal 0.01 
variable   KB equal 8.625e-5              
variable bars2Pa equal 1e5         
variable A2m equal 1.0e-10
variable ps2s equal 1.0e-12 
variable ev2J equal 96438.5/6.02214e23
variable g_mol2kg equal 1.0e-3/6.02214e23
variable    convert_eta equal ${g_mol2kg}/${ps2s}/${A2m} 

compute mytemp all temp/partial  0 0 1                 #The temperature is calculated after excluding the velocity components in x and y directions
fix fxnvt all nvt temp  100 100 1
fix_modify fxnvt temp mytemp                           #Removing the velocity component essentially calculates the temperature after the "bias" of the atomic velocity is removed

#The response is measured by the off diagonal component of the stress tensor proportional to the momentum flux.
fix MP_v all viscosity 10 x y 20                       #The momentum in the x direction is exchanged every 0.1ps, and the momentum transfer direction is the y direction
compute layers_eta all chunk/atom bin/1d y center 0.05 units reduced      #20 blocks in y direction
fix ave_vx all ave/chunk 20 50 1000 layers_eta vx file MP_vx.txt          #The output is the speed in the x direction

# equilibration run 

variable	dVx equal (2*f_ave_vx[11][3]-f_ave_vx[1][3]-f_ave_vx[20][3])/2             
thermo          1000
thermo_style	custom step temp pe ke etotal f_MP_v v_dVx               
thermo_modify temp mytemp                                
run		100000
unfix		MP_v

# data gathering run
fix		MP_v all  viscosity 10 x y 20
variable	eta equal -(f_MP_v/(2*((step-100000)*${dt})*lx*lz+1.0e-10))/(v_dVx/(ly/2))*${convert_eta}

thermo_style	custom step temp pe ke etotal f_MP_v v_dVx v_eta
thermo_modify temp mytemp

run	        100000

2.   x square towards speed degree ladder degree \Color {red} {2. \ velocity gradient in X direction} 2. Velocity gradient in x direction

3.   l o g writing piece in Department branch meter count junction fruit exhibition show \Color {red} {3. \ display of some calculation results in log file} 3. Display of some calculation results in the log file

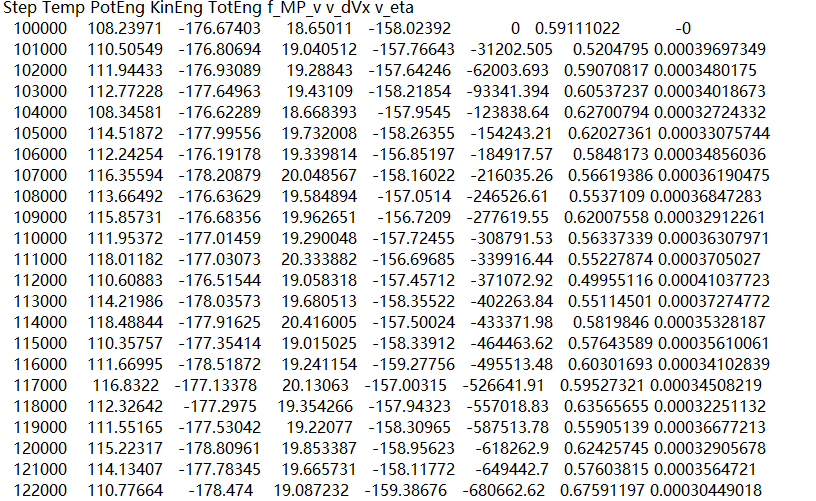
4, Summary

Share this time M P MP The principle of MP method for calculating viscosity and a calculation case are given. Friends who need to calculate shear viscosity can modify it directly on the basis of this code. If you have any questions, please communicate.

Tutorial / code download address( click here.)
Extraction code: yaek