I believe that friends with development experience have encountered such a demand. Suppose you are developing a comment function for a news website. Readers can comment on the original text and even reply to each other.

This demand is not simple. Replying to each other will lead to infinite branches and infinite ancestor offspring relationships. This is a typical recursive relational data.

For this problem, several solutions are given below, which you can choose after objective consideration.

1, Adjacency table: dependent parent node

The scheme of adjacency table is as follows (only to illustrate the problem):

CREATE TABLE Comments(
    CommentId int PK,
    ParentId　 int,　 --Record parent node　ArticleId　int,
    CommentBody nvarchar(500),
    FOREIGN KEY (ParentId)  REFERENCES Comments(CommentId)  --Self join. Primary keys and foreign keys are in their own tables　　　　
    FOREIGN KEY (ArticleId) REFERENCES Articles(ArticleId)
)

Due to laziness, the figure in the book is adopted. Bugs is Articles:

　　

This design method is called adjacency table. This is probably the most common solution for storing tiered data.

Here are some data to show the hierarchical data in the comment table. Example table:

　　

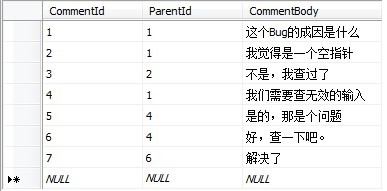
Picture description storage structure:

　　

Advantages and disadvantages analysis of adjacency table

For the above adjacency table, many programmers have taken it as the default solution, but even so, it still has problems in the past.

Analysis 1: how to query all descendants (subtrees) of a node?

Let's first look at the previous SQL statements for querying two-tier data:

SELECT c1.*,c2.* FROM Comments c1 LEFT JOIN Comments2 c2 ON c2.ParentId = c1.CommentId

Obviously, every time you need to check one more layer, you need to join the table one more time. The join times of SQL query are limited, so we can't get all descendants infinitely deep. Moreover, it is quite difficult to execute aggregation functions such as Count() in this connection.

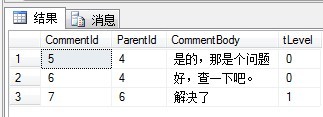
It's the past. What era is it now? After SQLServer 2005, a common table expression is solved. In addition, the problem of aggregate function (aggregate function such as Count() can also be simple and practical) is solved. For example, query all child nodes of comment 4:

WITH COMMENT_CTE(CommentId,ParentId,CommentBody,tLevel) AS (    --Basic statement
    SELECT CommentId,ParentId,CommentBody,0 AS tLevel FROM Comment WHERE ParentId = 4
    UNION ALL  --Recursive statement
    SELECT c.CommentId,c.ParentId,c.CommentBody,ce.tLevel + 1 FROM Comment AS c 
    INNER JOIN COMMENT_CTE AS ce  --recursive query 
    ON c.ParentId = ce.CommentId
)SELECT * FROM COMMENT_CTE

The display results are as follows:

　　

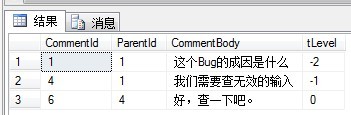
So how to query the ancestor node tree? For example, check all the ancestor nodes of node 6:

WITH COMMENT_CTE(CommentId,ParentId,CommentBody,tLevel) AS (    --Basic statement
    SELECT CommentId,ParentId,CommentBody,0 AS tLevel FROM Comment WHERE CommentId = 6
    UNION ALL
    SELECT c.CommentId,c.ParentId,c.CommentBody,ce.tLevel - 1 FROM Comment AS c 
    INNER JOIN COMMENT_CTE AS ce ON ce.ParentId = c.CommentId --recursive query 
    where ce.CommentId <> ce.ParentId   
)SELECT * FROM COMMENT_CTE ORDER BY CommentId ASC

The results are as follows:

　　

Moreover, because the common table expression can control the depth of recursion, you can simply obtain any level of subtree.

OPTION(MAXRECURSION 2)

It seems that brother came for the rehabilitation of adjacency table.

Analysis 2: of course, the adjacency table also has its advantages. For example, it is very convenient to add a record.

INSERT INTO Comment(ArticleId,ParentId)...  --Only the parent node needs to be provided Id Can be added.

Analysis 3: modifying the location of a node or a subtree is also very simple

UPDATE Comment SET ParentId = 10 WHERE CommentId = 6　--Modify only one node's ParentId，The subsequent child nodes are automatically reasonable.

Analysis 4: delete subtree

Imagine if you delete an intermediate node, what about the child nodes of the node (who are their parent nodes). Therefore, if you want to delete an intermediate node, you have to find all descendants and delete them first before deleting the intermediate node.

Of course, this process can also be automatically completed through a foreign key constraint of cascade deletion of ON DELETE CASCADE.

Analysis 5: delete intermediate nodes and promote child nodes

For the promoted child node, we need to modify the ParentId of the direct child node of the intermediate node before deleting the node:

SELECT ParentId FROM Comments WHERE CommentId = 6;　--Search for the parent node of the node to be deleted, assuming that 4 is returned
UPDATE Comments SET ParentId = 4 WHERE ParentId = 6;　--Modify the of the child node of the intermediate node ParentId To delete an intermediate node
ParentId DELETE FROM Comments WHERE CommentId = 6;  --Finally, the intermediate node can be deleted

From the above analysis, we can see that the adjacency table is basically very powerful.

2, Path enumeration

The design of path enumeration is to combine the information of all ancestors into a string and save it as an attribute of each node.

Path enumeration is a complete path composed of continuous direct hierarchical relationships. For example, "/ home/account/login", where home is the direct father of account, which means that home is the ancestor of login.

There is also the example of news review just now. We use path enumeration to replace the design of adjacency table:

CREATE TABLE Comments(
    CommentId int PK,
    Path varchar(100), --Only the field was changed and the foreign key was deleted　ArticleId int,
    CommentBody nvarchar(500),
    FOREIGN KEY (ArticleId) REFERENCES Articles(ArticleId)
)

The data sheet briefly describing the problem is as follows:

CommentId	Path	CommentBody
1	1/	What is the cause of this Bug
2	1/2/	I think it's a null pointer
3	1/2/3	No, I checked
4	1/4/	We need to check for invalid input
5	1/4/5/	Yes, that's a problem
6	1/4/6/	OK, check it out.
7	1/4/6/7/	Solved

Advantages of path enumeration:

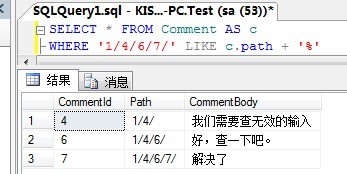
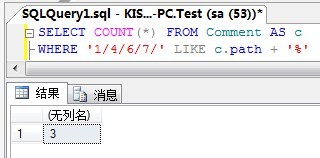
For the above table, suppose we need to query all the ancestors of a node. The SQL statement can be written as follows (suppose all the ancestors of query 7):

SELECT * FROM Comment AS cWHERE '1/4/6/7/' LIKE c.path + '%'

The results are as follows:

　　

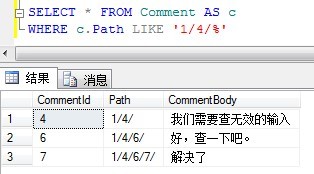
Suppose we want to query all descendants of a node. Suppose that the descendants of 4:

SELECT * FROM Comment AS cWHERE c.Path LIKE '1/4/%'

The results are as follows:

　　

Once we can easily obtain a subtree or the path from the descendant node to the ancestor node, we can easily implement more queries, such as calculating the number of all nodes in a word (COUNT aggregate function)

　　

Inserting a node can also be as simple as using an adjacency table. You can insert a leaf node without modifying any other rows. All you need to do is copy the logical parent node path of the node to be inserted, and append the Id of the new node to the end of the path. If the Id is generated by the database during insertion, you may need to insert the record first, then obtain the Id of the record and update its path.

Disadvantages of path enumeration:

1. The database cannot ensure that the format of the path is always correct or that the nodes in the path do exist (if the intermediate node is deleted, there is no foreign key constraint).

2. It is necessary to rely on high-level programs to maintain the string in the path, and it is very expensive to verify the correctness of the string.

3. It is difficult to determine the length of VARCHAR. No matter how large the length of VARCHAR is, it cannot be expanded indefinitely.

The design method of path enumeration can be easily sorted according to the hierarchy of nodes, because the distance between the nodes on both sides of the path is always 1. Therefore, the depth of the hierarchy can be known by comparing the string length.

3, Nested set

Nested set solution is to store the information of descendant nodes, not the direct ancestors of nodes. We use two numbers to encode each node to represent this information. You can call these two numbers nsleft and nsright.

Take the above news comments as an example. For nested sets, the table can be designed as follows:

CREATE TABLE Comments(
    CommentId int PK,
    nsleft int,  --Previous parent node
    nsright int,  --Into two　ArticleId　int,
    CommentBody nvarchar(500),
    FOREIGN KEY (ArticleId) REFERENCES Articles(ArticleId)
)

Determination of nsleft value: the value of nsleft is less than the Id of all descendants of the node.

Determination of nsright value: the value of nsright is greater than the Id of all descendants of the node.

Of course, the above two numbers are not related to the value of CommentId. The way to determine the value is to perform a depth first traversal of the tree, allocate the value of nsleft incrementally in the process of layer by layer, and allocate the value of nsright incrementally in return.

Use the diagram in the book to illustrate the following situation:

　　

Once you assign these numbers to each node, you can use them to find the ancestors and descendants of a given node.

Advantages of nested sets:

I think it's the only advantage. It's convenient to query ancestor trees and subtrees.

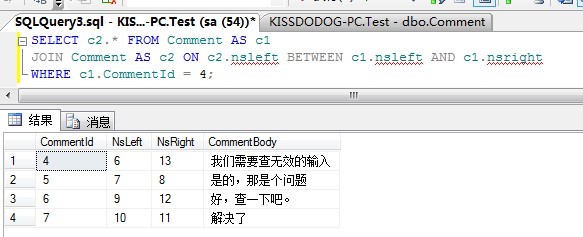
For example, by searching the concentid of those nodes, you can get them and all their descendants between nsleft and nsright in comment 4:

SELECT c2.* FROM Comments AS c1 
JOIN Comments AS c2 ON cs.neleft BETWEEN c1.nsleft AND c1.nsright 
WHERE c1.CommentId = 1;

The results are as follows:

　　

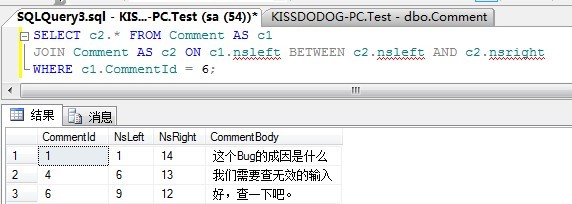
By searching which node's nsleft and nsright ranges the Id of comment 6 is, you can get comment 6 and all its ancestors:

SELECT c2.* FROM Comment AS c1 
JOIN Comment AS c2 ON c1.nsleft BETWEEN c2.nsleft AND c2.nsright 
WHERE c1.CommentId = 6;

　　

Another advantage of this nested set design is that when you want to delete a non leaf node, its offspring will automatically replace the deleted node, which is called the direct offspring of its direct ancestor node.

Nested set designs do not have to preserve hierarchical relationships. Therefore, when deleting a node causes numerical discontinuity, it will not have any impact on the structure of the tree.

Disadvantages of nested sets:

1. Query direct father.

In the design of nested sets, the idea of realizing this requirement is that the direct father of a given node c1 is an ancestor of this node, and there should be no other nodes between the two nodes. Therefore, you can query a node with a recursive extranet, which is the ancestor of c1 and the descendant of another node y, Then we make y=x query until the query returns null, that is, there is no such node. At this time, y is the direct parent node of c1.

For example, to find the direct parent node of comment 6: to be honest, the SQL statement is long and smelly. The line must be the line, but I really can't write it.

2. Operate on the tree, such as inserting and moving nodes.

When inserting a node, you need to recalculate the adjacent siblings, ancestors and brothers of its ancestors of the newly inserted node to ensure that their left and right values are greater than the left value of the new node. At the same time, if the new node is a non leaf node, you also need to check its descendant nodes.

Enough, enough. It is difficult to check the direct parent node, which is very popular. I'm sure I won't use this design.

4, Closure table

Closure table is a simple and elegant solution for tiered storage. It records all node relationships in the table, not just direct parent-child relationships.
In the design of closure table, an additional TreePaths table (space for time) is created, which contains two columns. Each column is a foreign key pointing to the CommentId in Comments.

CREATE TABLE Comments(
    CommentId int PK,
    ArticleId int,
    CommentBody int,
    FOREIGN KEY(ArticleId) REFERENCES Articles(Id)
)

Parent child relationship table:

CREATE TABLE TreePaths(
    ancestor int,
    descendant int,
    PRIMARY KEY(ancestor,descendant), --Composite primary key
    FOREIGN KEY (ancestor) REFERENCES Comments(CommentId),
    FOREIGN KEY (descendant) REFERENCES Comments(CommentId)
)

In this design, the Comments table will no longer store the tree structure, but store the ancestor descendant relationship in the book as a row of TreePaths, even if there is no direct parent-child relationship between the two nodes; At the same time, a line is added to point to the node itself. Can't you understand? It is the TreePaths table that stores records of all ancestor offspring relationships. As shown below:

　　

Comment table:

　　

TreePaths table:

　　

advantage:

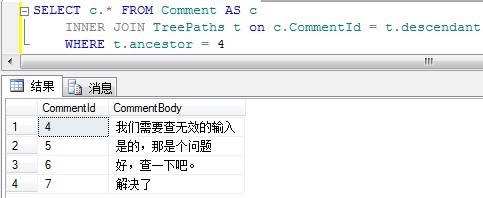
1. Query all descendant nodes (query tree):

SELECT c.* FROM Comment AS c INNER JOIN TreePaths t on c.CommentId = t.descendant 
WHERE t.ancestor = 4

The results are as follows:

　　

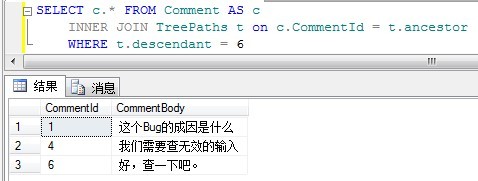
2. Query all ancestors of comment 6 (query ancestor tree):

SELECT c.* FROM Comment AS c INNER JOIN TreePaths t on c.CommentId = t.ancestor 
WHERE t.descendant = 6

The display results are as follows:

　　

3. Insert new node:

To insert a new leaf node, you should first insert a relationship between yourself and yourself, then search the node in the TreePaths table where the descendant is comment 5, and add the "ancestor descendant" relationship between the node and the new node to be inserted.

For example, the following is the TreePaths TABLE statement for inserting a child node of comment 5:

INSERT INTO  TreePaths(ancestor,descendant) SELECT t.ancestor,8 FROM TreePaths AS t 
    WHERE t.descendant = 5 
    UNION ALL 
    SELECT 8,8

After execution:

　　

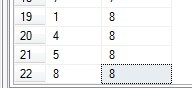
As for the Comment table, it's too simple to say.

4. Delete leaf node:

For example, to delete leaf node 7, delete all rows with descendant 7 in the TreePaths table:

DELETE FROM TreePaths WHERE descendant = 7

5. Delete subtree:

To delete a complete subtree, such as comment 4 and all its descendants, delete all rows with descendants of 4 in the TreePaths table and those with descendants of comment 4 as descendants:

DELETE FROM TreePaths 
WHERE descendant IN(SELECT descendant FROM TreePaths WHERE ancestor = 4)

In addition, for mobile nodes, it is not difficult to write SQL statements that first disconnect the relationship with the original ancestor and then establish a relationship with the new node.

In addition, the closure table can also be optimized, such as adding a path_ In the length field, the self reference is 0, the direct child node is 1, and the lower layer is 2. By analogy, the query directly from the child node becomes very simple.

summary

In fact, in previous work, I have seen different types of designs, such as adjacency table, path enumeration, adjacency table and path enumeration.

Each design has its own advantages and disadvantages. If the choice of design depends on which operation in the application needs performance optimization most. 　

A table is given below to show the difficulty of various designs:

Design	Number of tables	Query sub	Query tree	insert	delete	Referential integrity
Adjacency table	1	simple	simple	simple	simple	yes
Enumeration path	1	simple	simple	simple	simple	no
Nested set	1	difficulty	simple	difficulty	difficulty	no
Closure table	2	simple	simple	simple	simple	yes

1. Adjacency table is the most convenient design, and many software developers know it. With the help of recursive query, the query of adjacency table is more efficient.

2. Enumerating paths can intuitively show the paths from ancestors to descendants, but the design is fragile because the referential integrity cannot be guaranteed. Enumeration paths also make the storage of data redundant.

3. Nested set is a smart solution, but it cannot ensure referential integrity, and can only be used in situations where query performance is high and other requirements are general.

4. Closure table is the most common design, and it is the most flexible and easy to expand. Moreover, a node can belong to multiple trees, which can reduce the redundant calculation time. But it requires an additional table to store relationships, which is a scheme of space for time.