Original text from:< Old cake explanation neural network >

catalogue

I Normalization and inverse normalization

II Practical examples

III Complete code example

IV Inverse normalization of network expression

In order to facilitate better network training, the input and output data will be normalized before training. After training, when using network prediction, it is also necessary to inverse normalize the predicted value of the network.

This paper describes the normalization and inverse normalization of neural networks

I Normalization and inverse normalization

Before training, in order to avoid the large order of magnitude difference of each input variable and affect the effect of the solution algorithm, the data will generally be normalized to the interval of [- 1,1].

PASS: the benefits of normalization are not just to avoid orders of magnitude. See the article for details< Why should neural networks be normalized >

(1) Normalization formula of data before training

(2) When used, y is inversely normalized

Because we use the normalized data for training. Therefore, the network is aimed at the normalized data.

Therefore, when we use the trained network to make prediction, the input and output must be subject to data conversion. We need to:

(1) Input normalization during prediction

(2) Inverse normalization of output

Output inverse normalization function:

 

II Practical examples

1. Normalize the data before training

Suppose our original data are as follows:

x1	5	-2	3	8
x2	4	2	1	6
y	0	5	2	-5

knowable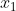If the maximum value of is 8 and the minimum value is - 2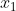The normalized values are as follows:

Original data: x1	5	-2	3	8
After normalization: (x1-(-1)) / (8-(-2))-1	0.4	-1	0	1

Same treatment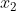 And y, the normalized data are as follows:

Normalized data
x1	0.4	-1	0	1
x2	0.2	-0.6	-1	1
y	0	1	0.4	-1

2. Anti normalization during use after training

For example, to predict X1 = 2 and X2 = 3, do the following:

(1) First normalize X1 and X2, and then input them into the network

When normalizing, we know that the maximum value of x1 is 8, the minimum value is - 2, the maximum value of x2 is 6, and the minimum value is 1,

Then the normalized values of X1 and X2 are:

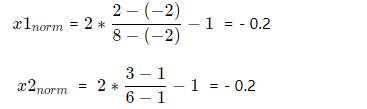
The value of input network during prediction is sim(net,[-0.2,-0.2])

(2) It is assumed that the above network output is 0.5, but this is for normalized data. In order to obtain the real predicted value, we need to reverse normalization.

When normalizing, we know that the maximum value of y is 5 and the minimum value is - 5,

Then y:

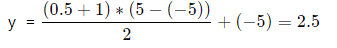
III Complete code example

x1 = linspace(-3,3,100);           % stay[-3，3]Generate 100 data linearly between
x2 = linspace(-2,1.5,100);         % stay[-2，1.5]Generate 100 data linearly between
y = sin(x1)+0.2*x2.*x2;            % generate y

inputData  = [x1;x2];              % take x1,x2 As input data
outputData = y;                    % take y As output data

%Normalization:
inputMax = max(inputData,[],2);    % Maximum value entered
inputMin = min(inputData,[],2);    % Minimum value entered

outputMax = max(outputData,[],2);  % Maximum value of output
outputMin = min(outputData,[],2);  % Minimum value of output

[varNum,sampleNum] = size(inputData);
inputDataNorm  = inputData;        % initialization inputDataNorm
outputDataNorm = outputData;       % initialization outputDataNorm

%Normalize
for i = 1 : sampleNum
 inputDataNorm(:,i)  = 2*(inputData(:,i)-inputMin)./(inputMax-inputMin)-1;   
 outputDataNorm(:,i) = 2*(outputData(:,i)-outputMin)./(outputMax-outputMin)-1;      
end

%Use input / output data( inputDataNorm,outputDataNorm)Establish the network and set the number of hidden nodes to 3.The nodes from the input layer to the hidden layer and from the hidden layer to the output layer are tansig and purelin，use trainlm Method training.
net = newff(inputDataNorm,outputDataNorm,3,{'tansig','purelin'},'trainlm');

%Set some common parameters
net.trainparam.goal = 0.0001;     % Training objective: the mean square error is less than 0.0001
net.trainparam.show = 400;        % Show results every 400 workouts
net.trainparam.epochs = 15000;    % Maximum training times: 15000.

[net,tr] = train(net,inputDataNorm,outputDataNorm);%call matlab Neural network toolbox comes with train Function training network

figure;

%Fitting effect of training data
simoutNorm = sim(net,inputDataNorm);
%Inverse normalization:

simout=(simoutNorm+1).*(outputMax-outputMin)/2+outputMin;

title('Neural network prediction results')
hold on
t=1:length(simout);
plot(t,outputData,t,simout,'r')%Draw a picture and compare it with the original one y And network prediction y

IV Inverse normalization of network expression

After the neural network is normalized, the trained model coefficients correspond to the normalized data. In order to obtain the model coefficients corresponding to the original data, the model coefficients need to be de normalized. See< Inverse normalization of network expression>