New solution of sequence query

Topic background

The previous question "sequence query" said: A=[A0,A1,A2 ···, An] is a sequence composed of n+1 integers in the range of [0,N], which satisfies 0 = A0 < A1 < A2 < ·· < An < n. Based on sequence a, for any integer x within the range of [0,N], the query f(x) is defined as the subscript of the largest number of integers less than or equal to X in sequence a.

For A given sequence A and integer x, the query f(x) is A very classic problem, which can be easily solved within the time complexity of O(log n) using binary search. But when the IT Department discussed how to realize this function, little P put forward some new ideas.

Title Description

Input format

Read in data from standard input.

The first line of input contains two positive integers n and N separated by spaces.

The second line of input contains n integers A1,A2, ···, AN separated by spaces.

Note that A0 is fixed to 0, so A0 is not included in the input data.

Output format

Output to standard output.

Only one integer is output to represent the value of error(A).

Example 1 input

3 10
2 5 8

Sample 1 output

5

Example 1 explanation

Example 2 Input

9 10
1 2 3 4 5 6 7 8 9

Sample 2 output

0

Sample input 3

2 10
1 3

Sample 3 output

6

Sample 3 output

Subtask

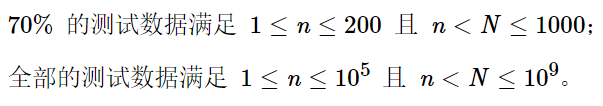
Tips

It should be noted that the input data [A1,A2 ····, An] are not necessarily evenly distributed in the (0,N) interval, so the total error(A) may be very large.

code

#include <bits/stdc++.h>
using namespace std;
long long n, N;
const long long Maxn = 1e5 + 5;
long long arr[Maxn] = { 0 };
long long vi[Maxn] = { 0 };
long long r;
long long num = 0;
long long add(long long first, long long count) {//First represents the first g (x) - f (x), and count represents that the interval contains several equally divided intervals
    long long last = first + count - 1;//Last term, if the interval is in an average partition, last is equal to 2*first
    long long final;
    if (last * first >= 0)//The same symbol indicates that the starting point and the ending point are in the same partition
        return final = abs((first + last) * count / 2 * r);//That is, the sum of all absolute values from the starting point to the end is calculated, * r represents all sums in the interval
    else//Different symbols, first is a negative number, indicating that the two points are not in the same partition
        return final = (abs(first) + 1) * abs(first) / 2 * r + last * (last + 1) / 2 * r;//Calculate positive and negative numbers separately
}
int main()
{
    cin >> n >> N;
    arr[0] = 0;
    long long lea = 0;//Represents the final result
    long long co,k;
    r = N / (n + 1);
    for (long long i = 1; i <= n; i++) {
        cin >> arr[i]; 
        vi[i] = arr[i] - arr[i - 1];//Using vi array to store the length of interval
    }
    vi[n+1]= N - arr[n];//The length of the section in which the last read data is stored is greater than the last read data
    for (long long i = 1; i <= n+1; i++) {
        co = (vi[i]+ lea)/r;//Calculate how many equal intervals the current interval is equivalent to
        k = arr[i - 1] / r;//Calculate the value corresponding to g(x) of the first element at the beginning of the interval
        num += add(k - i + 1, co);//Calculate and add the error value of the interval
        if(k-i+1>=0)num += lea;//If G (x) > F (x) of the current interval, add the number of extra numbers between the average partitions
        else num -= lea;//Otherwise, the current interval subtracts the number of extra digits in the average partition
        lea = (vi[i] + lea) % r;//lea indicates the number of numbers not in the first part of the partition
    }
    k += co;
    num += abs(k - n) * lea;//Finally, add the absolute value of the difference between g(x) and f(x) multiplied by the number of remaining uncomputed numbers
    cout<<num;
    return 0;
}

thinking

The idea is to calculate the r in the topic first, and divide the section of [0,N] into N/r equally divided sections. In the corresponding section, the values of g(x) corresponding to all numbers are the same. Then, another segmentation is carried out for the section of [0,N] through the read array. This segmentation determines f(x) and divides the same number of f(x) into an interval. Then, take one segment of the second segment each time, judge whether the left and right ends of the interval belong to the same equally divided interval, then judge the positive and negative of the difference between g(x) and f(x) in the interval, then calculate the sum of the absolute values of the difference in the interval, and finally cycle calculation.