What is text clustering?
Text clustering is to transform the original natural language text information into mathematical information, which is displayed in the form of high-dimensional spatial points. By calculating the distance between those points, those points are clustered into a cluster, and the center of the cluster is called the cluster center. A good clustering should ensure that the distance between the points in the cluster is as close as possible, but the points between clusters should be as far as possible.
What are the difficulties of text clustering?
Clustering is a kind of unsupervised learning, that is to say, we don't know how to cluster into several categories, and we can only try it out a little bit. However, sometimes machines think that these two piles of points can be regarded as two clusters, but human understanding may be one cluster, so text clustering is difficult. The understanding of machines and people is different. Generally, people who can see this blog have learned the basic clustering algorithm. Take k-means as an example. The selection of cluster center is a very random process, resulting in different clustering results every time when the k value is the same, and it is not easy to take an average, so it is difficult to evaluate the quality of clustering.
How to evaluate clustering?
http://blog.csdn.net/chixujohnny/article/details/51852633 S, who talked about everything_ I haven't tried the DBW evaluation index yet. Students who are interested can try it. In short, it should be used sooner or later.
Text clustering process
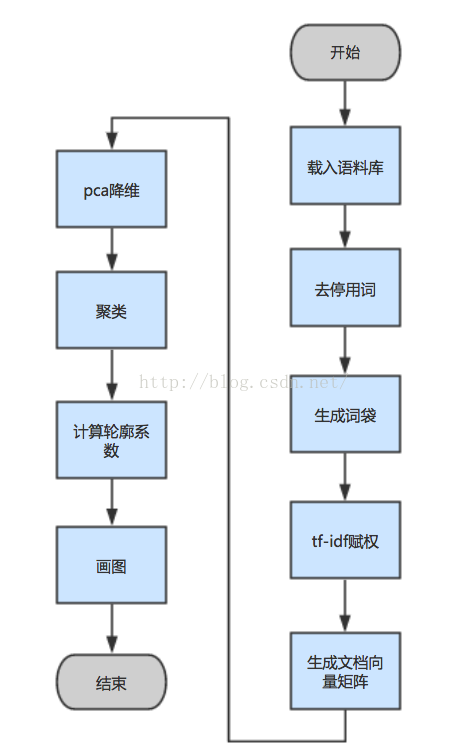
Word weighting method and textrate are useless. jieba comes with it. It looks good to the naked eye. You can try it.
The above figure shows several parts. Generally, the format of generating document vector matrix is that each row represents a document, and each column is a dimension, representing the weight of the word "document". If the word does not appear, it is 0, and thousands of file dimensions are more than 10 w Left and right (see the size of the document). With such a large dimension, the human brain thought and thought that the matrix would be extremely sparse. That is to say, in a high-dimensional space, thousands of points almost gather together. Although there is a distance between them, the distance is very small. Obviously, the clustering effect must be very poor. It has been measured, which is the same as the probability of coin tossing. So I thought of making the matrix a little denser pca Dimensionality reduction, pca It is the abbreviation of principal component analysis, which roughly means to take the direction with the largest variance in this high-dimensional vector, retain the useful part and discard the useless part after some mathematical transformation. This method is also suitable for finding the most hanging features in the classification algorithm. The specific details I saw in the book "machine learning practice" (the book of a little brother carrying a sack), I didn't speak in detail, but I understood it roughly. Why not SVD Dimensionality reduction, SVD Suitable for dense matrix, such as image matrix or recommendation system, take 80%Useful information, suitable for image compression algorithm (if you don't know deeply, please slap your face). I actually saw the concept of contour coefficient in the blog of this Beiyou student: buptguo.com/2016/05/31/learn-ml-from-scikit-learn-silhouette-analysis/ Just click in and have a look. He speaks better than me. I read some data about clustering. Those of Baidu are all used k-means Do text clustering, I just want to ask if you do school homework? Thousands of dimensional vectors k-means Do? Funny? I measured it, the effect is very poor, the accuracy of throwing the sieve. Later, I began to check the literature. One kind is called BIRCH Hierarchical clustering algorithm, the algorithm can be better solved k-means The deviation of each clustering result is too large dbscan The number of clusters can be set (of course, the threshold can also be set). The most important thing is sklearn There are ready-made library calls, and the speed is very fast. Give it a try, Billy kmeans OK, but I'm not particularly satisfied. After checking, it's still not suitable for high-dimensional space. I'm ready to check the data again.
There are several points that may need to be tried:
The threshold of clustering algorithm can be set. Try any other clustering algorithm, especially the high-dimensional clustering algorithm.
Assign the weight with textrate to see how the effect is
code:
# coding:utf-8
# 2.0 use jieba for word segmentation, completely abandon the inefficient NLPIR, and assign the weight with textrank algorithm (the measured textrank effect is better)
# 2.1 make tfidf with gensim
# 2.2 sklearn does tfidf and kmeans
# 2.3 change kmeans to BIRCH and use traditional tfidf
import logging
import time
import os
import jieba
import glob
import random
import copy
import chardet
import gensim
from gensim import corpora,similarities, models
from pprint import pprint
import jieba.analyse
from sklearn import feature_extraction
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.feature_extraction.text import CountVectorizer
import os
from sklearn.decomposition import PCA
# logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
start = time.clock()
print '#----------------------------------------#'
print '# #'
print '# Loading corpus #'
print '# #'
print '#----------------------------------------#\n'
def PreprocessDoc(root):
allDirPath = [] # The left and right folder paths under the corpus dataset folder, string,[1:] is the required path
fileNumList = []
def processDirectory(args, dirname, filenames, fileNum=0):
allDirPath.append(dirname)
for filename in filenames:
fileNum += 1
fileNumList.append(fileNum)
os.path.walk(root, processDirectory, None)
totalFileNum = sum(fileNumList)
print 'The total number of documents is: ' + str(totalFileNum)
return allDirPath
print '#----------------------------------------#'
print '# #'
print '# Synthetic corpus document #'
print '# #'
print '#----------------------------------------#\n'
# Each document has one line, and the first word is the category of the document
def SaveDoc(allDirPath, docPath, stopWords):
print 'Start synthesizing corpus documents:'
category = 1 # Category of document
f = open(docPath,'w') # Put all the text together in this document
for dirParh in allDirPath[1:]:
for filePath in glob.glob(dirParh + '/*.txt'):
data = open(filePath, 'r').read()
texts = DeleteStopWords(data, stopWords)
line = '' # Reduce these words to one line. The first position is the document category, separated by spaces
for word in texts:
if word.encode('utf-8') == '\n' or word.encode('utf-8') == 'nbsp' or word.encode('utf-8') == '\r\n':
continue
line += word.encode('utf-8')
line += ' '
f.write(line + '\n') # Write this line into the file
category += 1 # After scanning a folder, category + 1
return 0 # Generate document without return value
print '#----------------------------------------#'
print '# #'
print '# participle+De stop word #'
print '# #'
print '#----------------------------------------#\n'
def DeleteStopWords(data, stopWords):
wordList = []
# Divide the words first
cutWords = jieba.cut(data)
for item in cutWords:
if item.encode('utf-8') not in stopWords: # The word segmentation code shall be consistent with the stop word code
wordList.append(item)
return wordList
print '#----------------------------------------#'
print '# #'
print '# tf-idf #'
print '# #'
print '#----------------------------------------#\n'
def TFIDF(docPath):
print 'start tfidf:'
corpus = [] # Document corpus
# Read the corpus, and one line of corpus is a document
lines = open(docPath,'r').readlines()
for line in lines:
corpus.append(line.strip()) # There are no spaces before and after strip(), but the middle space is still reserved
# Convert the words in the text into word frequency matrix, and the matrix element a[i][j] represents the word frequency of j words under class I text
vectorizer = CountVectorizer()
# This class will count the tfidf weight of each word
transformer = TfidfTransformer()
# First fit_transform is the second fit to calculate TF IDF_ Transform is to convert text into word frequency matrix
tfidf = transformer.fit_transform(vectorizer.fit_transform(corpus))
# Get all words in the word bag model
word = vectorizer.get_feature_names()
# The TF IDF matrix is extracted, and the element w[i][j] represents the TF IDF weight of j words in class I text
weight = tfidf.toarray()
print weight
# # Output all words
# result = open(docPath, 'w')
# for j in range(len(word)):
# result.write(word[j].encode('utf-8') + ' ')
# result.write('\r\n\r\n')
#
# # Output all weights
# for i in range(len(weight)):
# for j in range(len(word)):
# result.write(str(weight[i][j]) + ' ')
# result.write('\r\n\r\n')
#
# result.close()
return weight
print '#----------------------------------------#'
print '# #'
print '# PCA #'
print '# #'
print '#----------------------------------------#\n'
def PCA(weight, dimension):
from sklearn.decomposition import PCA
print 'Original dimension: ', len(weight[0])
print 'Start dimensionality reduction:'
pca = PCA(n_components=dimension) # Initialize PCA
X = pca.fit_transform(weight) # Return dimension reduced data
print 'Dimensionality after dimensionality reduction: ', len(X[0])
print X
return X
print '#----------------------------------------#'
print '# #'
print '# k-means #'
print '# #'
print '#----------------------------------------#\n'
def kmeans(X, k): # X=weight
from sklearn.cluster import KMeans
print 'Start clustering:'
clusterer = KMeans(n_clusters=k, init='k-means++') # Set clustering model
# X = clusterer.fit(weight) # According to the text vector fit
# print X
# print clf.cluster_centers_
# Cluster to which each sample belongs
y = clusterer.fit_predict(X) # Throw the weight matrix into fit and output label
print y
# i = 1
# while i <= len(y):
# i += 1
# It is used to evaluate whether the number of clusters is appropriate. The better the distance is, the number of clusters at the critical point is selected
# print clf.inertia_
return y
print '#----------------------------------------#'
print '# #'
print '# BIRCH #'
print '# #'
print '#----------------------------------------#\n'
def birch(X, k): # Lattice to be clustered, number of clusters
from sklearn.cluster import Birch
print 'Start clustering:'
clusterer = Birch(n_clusters=k)
y = clusterer.fit_predict(X)
print 'Output clustering results:'
print y
return y
print '#----------------------------------------#'
print '# #'
print '# Contour coefficient #'
print '# #'
print '#----------------------------------------#\n'
def Silhouette(X, y):
from sklearn.metrics import silhouette_samples, silhouette_score
print 'Calculate contour coefficient:'
silhouette_avg = silhouette_score(X, y) # Average contour coefficient
sample_silhouette_values = silhouette_samples(X, y) # Contour coefficient of each point
pprint(silhouette_avg)
return silhouette_avg, sample_silhouette_values
print '#----------------------------------------#'
print '# #'
print '# Draw a picture #'
print '# #'
print '#----------------------------------------#\n'
def Draw(silhouette_avg, sample_silhouette_values, y, k):
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
# Create a subplot with 1-row and 2-column
fig, ax1 = plt.subplots(1)
fig.set_size_inches(18, 7)
# First subplot contour coefficient point
# The range is [- 1, 1]
ax1.set_xlim([-0.2, 0.5])
# The following (k + 1) * 10 is to show these points more clearly
ax1.set_ylim([0, len(X) + (k + 1) * 10])
y_lower = 10
for i in range(k): # Traverse these clusters respectively
ith_cluster_silhouette_values = sample_silhouette_values[y == i]
ith_cluster_silhouette_values.sort()
size_cluster_i = ith_cluster_silhouette_values.shape[0]
y_upper = y_lower + size_cluster_i
color = cm.spectral(float(i)/k) # Make a color
ax1.fill_betweenx(np.arange(y_lower, y_upper),
0,
ith_cluster_silhouette_values,
facecolor=color,
edgecolor=color,
alpha=0.7) # I don't know what this coefficient does
# Add the cluster category number to the contour coefficient point
ax1.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
# Calculate the y of the next point_ Lower Y-axis position
y_lower = y_upper + 10
# Make a vertical dotted line in the figure
ax1.axvline(x=silhouette_avg, color='red', linestyle="--")
plt.show()
if __name__ == "__main__":
root = '/Users/John/Desktop/test'
stopWords = open('/Users/John/Documents/NLPStudy/stopwords-utf8', 'r').read()
docPath = '/Users/John/Desktop/test/doc.txt'
k = 3
allDirPath = PreprocessDoc(root)
SaveDoc(allDirPath, docPath, stopWords)
weight = TFIDF(docPath)
X = PCA(weight, dimension=800) # Dimensionality reduction of original weight data
# y = kmeans(X, k) # y = class label after clustering
y = birch(X, k)
silhouette_avg, sample_silhouette_values = Silhouette(X, y) # Contour coefficient
Draw(silhouette_avg, sample_silhouette_values, y, k)
end = time.clock()
print 'Running time: ' + str(end - start)
reference material:
Text clustering tutorial