Description:

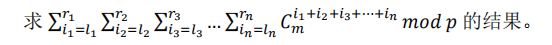
p < = 10 and p is prime, n < = 7, l, R < = 1e18

Explanation:

Lucas theorem:

\(C_{n}^m=C_{n~mod~p}^{m~mod~p}*C_{n/p}^{m/p}\)

If \ (n,m \) is decomposed in the p-base, it is \ (\ prod C {n [i]} ^ {m [i]} \).

For \ (∈ [l,r] \), the restriction is \ (< R \).

Considering the digit dp from the low to the high bit, set \ (f[i][S][j] \) to indicate that the first I bit has been made, and the number selected for the i-th number of S[i] is < = or >, and enter the coefficient sum of the j-bit.

If you want to transfer, you can enumerate what is selected for each digit. Of course, enumeration is < = or >, which is slow.

Let's use another dp to transfer. Let \ (g[i][S][j] \) denote that the number of the first I is considered. Now the state of pressure is s, the sum of this bit is j, and the initial value is \ (g[0][S][j]=f[i][S][j] \).

So the total time complexity is about \ (O (2 ^ n * log \ p ^ m * 2 ^ n * (PN) ^ 2) \)

It's a good run anyway.

Code:

#include<bits/stdc++.h>
#define fo(i, x, y) for(int i = x, B = y; i <= B; i ++)
#define ff(i, x, y) for(int i = x, B = y; i <  B; i ++)
#define fd(i, x, y) for(int i = x, B = y; i >= B; i --)
#define ll long long
#define pp printf
#define hh pp("\n")
using namespace std;

int jx[11][11];
int n, p;
ll m, l[101], r[11], a[11];
int b[101], b0, c[11][101], c0[11];
int a2[10];
int ans;
int f[2][1 << 7][8], o;
int g[2][1 << 7][60], o2;

#define mem(a) memset(a, 0, sizeof a)
void dp(int xs) {
    mem(c);
    fo(i, 1, n) {
        ll v = a[i];
        c0[i] = 0;
        for(; v > 0; v /= p) c[i][++ c0[i]] = v % p;
    }
    mem(f); f[o][0][0] = 1;
    fo(i, 1, b0) {
        mem(f[!o]);
        mem(g);
        ff(j, 0, a2[n]) fo(k, 0, n - 1) g[o2][j][k] = f[o][j][k];
        fo(j, 1, n) {
            mem(g[!o2]);
            ff(s, 0, a2[n]) fo(k, 0, 48) if(g[o2][s][k]) {
                g[o2][s][k] %= p;
                int s2 = s & (a2[n] - 1 - a2[j - 1]); 
                int ns = s2;
                int l = 0, r = c[j][i] - 1;
                fo(u, l, r) g[!o2][ns][k + u] += g[o2][s][k];
                ns = s;
                l = r = c[j][i];
                g[!o2][ns][k + l] += g[o2][s][k];
                ns = s2 + a2[j - 1];
                l = c[j][i] + 1, r = p - 1;
                fo(u, l, r) g[!o2][ns][k + u] += g[o2][s][k];
            }
            o2 = !o2;
        }
        ff(s, 0, a2[n]) fo(k, 0, 48) {
            f[!o][s][k / p] += g[o2][s][k] * jx[b[i]][k % p];
        }
        ff(s, 0, a2[n]) fo(k, 0, p - 1) f[!o][s][k] %= p;
        o = !o;
    }
    ff(s, 0, a2[n]) {
        int ky = 1;
        fo(j, 1, n) if((s >> (j - 1) & 1) && c0[j] <= b0) { ky = 0; break;}
        if(ky) ans = (ans + f[o][s][0] * xs) % p;
    }
}

void dg(int x, int xs) {
    if(x > n) {
        dp(xs);
        return;
    }
    a[x] = l[x] - 1; dg(x + 1, -xs);
    a[x] = r[x]; dg(x + 1, xs);
}

int main() {
    freopen("combination.in", "r", stdin);
    freopen("combination.out", "w", stdout);
    fo(i, 0, 7) a2[i] = 1 << i;
    scanf("%d %lld %d", &n, &m, &p);
    fo(i, 0, 10) {
        jx[i][0] = 1;
        fo(j, 1, i) jx[i][j] = (jx[i - 1][j - 1] + jx[i - 1][j]) % p;
    }
    fo(i, 1, n) scanf("%lld %lld", &l[i], &r[i]);
    for(; m; m /= p) b[++ b0] = m % p;
    dg(1, 1);
    ans = (ans % p + p) % p;
    pp("%d\n", ans);
}