T2: Given an undirected graph with n points and m edges, find the necessary points from 1 to n.

(n <= 200,000 m <== 2*n) (there may be self-rings and double edges)

At first glance, it is obvious that naked tarjan, happy heart 5 minutes to complete the tarjan cut point board, output all cut points, and then run through the sample to see T3:)

T3 can't imagine, idle boredom began to build T2 data, and as a result, a random group of them killed themselves...

As shown in the figure:

　　

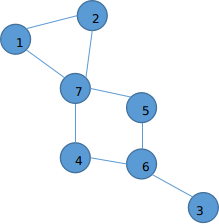
An awkward discovery is not necessarily a cut-off point!

So Ctrl+A, Delete:(

(Refactoring is good o_o#)

 

To reconstruct, we still need tarjan, which involves cut points, but is not a simple calculation and judgment, that is, point double shrinkage points or square trees.

Nevertheless, after learning the garden square tree, I have never written double-indentation points which are complex, detailed, space-occupying and difficult to write.

So I began to think about how to use the square tree to calculate the answer.

　　

Because the square tree will turn the original picture into a tree, it is easy to find that the answer is the dots on the chain from 1 to n on the square tree.

So it's done.

 

What? You said you couldn't make a square tree?

Laikang Little Pink Rabbit's Blog

　　

What? You don't tarjan yet? Please skip this question...

　　

　　

 1 #include<cstdio>
 2 #include<iostream>
 3 #include<cmath>
 4 #include<algorithm>
 5 #include<cstring>
 6 #include<vector>
 7 #include<queue>
 8 #define ll long long
 9 using namespace std;
10 const int MAXN=200005;
11 int T,n,m,dfn[MAXN],low[MAXN],stk[MAXN],fa[MAXN*2],num,tp,dcc_cnt;
12 bool flag;
13 inline int R() {
14     int a=0;char c=getchar();
15     while(c>'9'||c<'0')c=getchar();
16     while(c>='0'&&c<='9')a=a*10+c-'0',c=getchar();
17     return a;
18 }
19 struct node {
20     int to,nxt;
21 }mp[MAXN*8];
22 int h[MAXN*2],tot;
23 void add(int x,int y) {
24     mp[++tot].to=y;mp[tot].nxt=h[x];h[x]=tot;
25 }
26 void tarjan(int u) {
27     dfn[u]=low[u]=++num;
28     stk[++tp]=u;
29     for(int i=h[u];i;i=mp[i].nxt) {
30         int v=mp[i].to;
31         if(!dfn[v]) {
32             tarjan(v);
33             low[u]=min(low[u],low[v]);
34             if(low[v]==dfn[u]) {
35                 ++dcc_cnt;
36                 int tmp;
37                 do {
38                     tmp=stk[tp--];
39                     add(dcc_cnt+n,tmp); add(tmp,dcc_cnt+n);
40                 }while(tmp!=v);
41                 add(dcc_cnt+n,u); add(u,dcc_cnt+n);
42             }
43         }
44         else low[u]=min(low[u],dfn[v]);
45     }
46 }
47 void dfs(int u) {
48     if(u==n) {
49         flag=1;
50         return;
51     }
52     for(int i=h[u];i;i=mp[i].nxt) {
53         int v=mp[i].to;
54         if(v==fa[u]||(u<=n&&v<=n)) continue;
55         fa[v]=u;
56         dfs(v);
57         if(flag) return;
58     }
59 }
60 int main() {
61     T=R();
62     while(T--) {
63         n=R();m=R();
64         for(int i=1,aa,bb;i<=m;i++) {
65             aa=R(),bb=R();
66             add(aa,bb); add(bb,aa);
67         }
68         tarjan(1);
69         dfs(1);
70         int p=fa[n];
71         tp=0;
72         while(p!=1) {
73             if(p<n) stk[++tp]=p;
74             p=fa[p];
75         }
76         sort(stk+1,stk+tp+1);
77         printf("%d\n",tp);
78         for(int i=1;i<=tp;i++) printf("%d ",stk[i]);
79         printf("\n");
80         memset(dfn,0,sizeof(dfn));
81         memset(low,0,sizeof(low));
82         memset(h,0,sizeof(h));
83         memset(fa,0,sizeof(fa));
84         num=0;tot=0;tp=0;flag=0;dcc_cnt=0;
85     }
86     return 0;
87 }

t2 Code