Title Description

Flappy Bird is a popular casual mobile game. Players need to constantly control the frequency of clicking on the screen to adjust the bird's flight altitude, so that the bird can smoothly pass through the gap in the pipeline on the right side of the screen. If a bird accidentally bumps into a water pipe or falls to the ground, it fails.

In order to simplify the problem, we simplify and modify the rules of the game.

1. The game interface is a two-dimensional plane with a length of n and a height of m, in which there are k pipes (ignoring the width of the pipes).

2. Birds always move in the game interface. The bird starts at any integer height on the left side of the game interface and arrives at the right side of the game interface. The game is completed.

3. The distance of each bird moving to the right along the abscissa direction per unit time is 1, and the distance of vertical movement is controlled by the player. If you click on the screen, the bird will rise to a certain height X, each unit time can be clicked many times, the effect is superimposed;
If you don't click on the screen, the bird will drop to a certain height Y. When the bird is located in different positions in the abscissa direction, the rising height X and the falling height Y may be different from each other.

4. When the bird's height is equal to 0 or the bird touches the pipe, the game fails. When the bird's height is m, it can't rise any more.

Now, please judge if you can finish the game. If you can, output the least number of clicks on the screen; otherwise, output birds can pass through the maximum number of pipe slots.

Input and output format

Input format:

The input file is named bird.in.

Line 1 has three integers n, m and k, representing the length, height and number of pipes of the game interface, each of which has two integers.

Integers are separated by a space.

The next n rows, two integers X and Y separated by a space in each row, are represented in turn at the abscissa position of 0~n-1.

When the player clicks on the screen, the bird rises to the next position X, and when the player does not click on the screen at that position,

The height Y of the bird descending in the next position.

Next, k lines, each with three integers P, L, H, separated by a space between each two integers. Each line represents one

P represents the abscissa of the pipeline, L represents the height of the lower edge of the pipeline gap, H represents the pipeline gap.

The height of the upper edge (input data guarantees that P is different, but not given in order of size).

Output format:

The output file is named bird.out.

A total of two lines.

The first line contains an integer. If the game can be successfully completed, output 1, otherwise output 0.

The second line contains an integer. If the first action is 1, the number of screen clicks needed to complete the game successfully is minimum. Otherwise, how many slots can the output bird pass through?

Input and Output Samples

Input sample #1:

10 10 6
3 9
9 9
1 2
1 3
1 2
1 1
2 1
2 1
1 6
2 2
1 2 7
5 1 5
6 3 5
7 5 8
8 7 9
9 1 3

Output sample #1:

1
6

Input sample #2:

10 10 4
1 2
3 1
2 2
1 8
1 8
3 2
2 1
2 1
2 2
1 2
1 0 2
6 7 9
9 1 4
3 8 10

Output sample #2:

0
3

Explain

[Sample description of input and output]

As shown in the figure below, the blue line represents the bird's flight trajectory, and the red line represents the pipeline.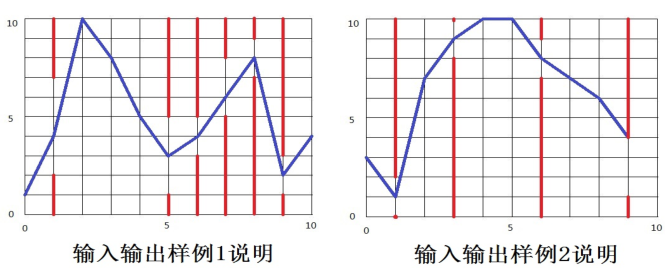

[Data Scope]

For 30% of the data: 5 < n < 10, 5 < m < 10, k = 0, there is a set of optimal solutions to ensure that the screen is clicked at most three times in the same unit time.

For 50% of the data: 5 < n < 20, 5 < m < 10, there is a set of optimal solutions to ensure that the screen is clicked three times at most in the same unit time.

For 70% of the data: 5 < n < 1000, 5 < m < 100;

For 100% data: 5 < n < 100 000, 5 < m < 100 00, 0 < K < n, 0

Thoughts (Draw lessons from xm dalao's PT)

For each coordinate on a non-pipeline, set it to (x, y), then enumerate the points with abscissa x-1.

If we can start from this point, then the equation of state transition is:

if(j>k&&(j-k)%up[i-1]==0)f[i][j]=min(f[i][j],f[i-1][k]+(j-k)/up[i-1]);

(Vertical coordinates are j and vertical coordinates of points with abscissa x-1 are k)

The state transition equation falling from above is better written. Find (x, y+down[i-1]) and write a state transition equation:

I f (k-down [i-1]== j) f [i] [j]= min (f [i] [j], f [i-1] [k]); (This is very understandable, I won't say much)

And then because it can't jump after jumping to the m boundary, we have to make a special judgment on this.

if(k==m&&down[i-1]==0)f[i][j]=min(f[i][j],f[i-1][k]);

else if(k==m&&down[i-1]!=0)f[i][j]=min(f[i][j],f[i-1][k]+1);

else {if((j-k)%up[i-1]==0)f[i][j]=min(f[i][j],f[i-1][k]+(j-k)/up[i-1]);

else f[i][j]=min(f[i][j],f[i-1][k]+(j-k)/up[i-1]+1);}

But if you do that, you will be overtime, and you can only get 70 points at most. Of course, if you write well, you can get 75 points.

The optimization here is a difficult point, it's hard to think about. The answer to each point can only be inferred from the next one.

For example, jump from column 3 to three squares in one step. (3,5) dp[3][5]=0 in this lattice, then (4,11) how to find it?

dp[4][8]=min(dp[4][8]，min(dp[3][5]，dp[4][5])+1)=1

dp[4][11]=min (dp[4][11], min (dp[3][8], dp[4][8]) +1) = 2 state transition equation:

dp[i][j]=min(dp[i][j],dp[i-1][j-up[i-1]]+1);

dp[i][j]=min(dp[i][j],dp[i][j-up[i-1]]+1);

Drop and Special Judgement are the same as before, but pay attention to one thing: the rise should be written before the fall, otherwise the rise may be deduced from the fall, max=80 points!

In this way, O (nano ^ 2) is reduced to O (nano), and the 100-minute program is written!

Seventy versions of the code (not written by myself)

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
const int maxn=10000+10,maxm=1000+10;  //Easy to write
int n,m,i,j,k,pipe,f[maxn][maxm],x;
struct apipe{int downpos,uppos;};
int up[maxn],down[maxn]; apipe p[maxn];
void readdata()  //Read in data, initialize
{
    scanf("%d %d %d",&n,&m,&pipe); for(i=0;i<n;i++)scanf("%d %d",&up[i],&down[i]);
    for(i=0;i<=n;i++){p[i].downpos=-1; p[i].uppos=m+1;}
    for(i=1;i<=pipe;i++){scanf("%d",&x); scanf("%d %d",&p[x].downpos,&p[x].uppos);}
    for(i=0;i<=m;i++)f[0][i]=0;  //Take-off at Arbitrary Height in the First Row
}
bool check(int x,int y)  //Not in the pipeline anymore.
{
    if(p[x].downpos<y&&p[x].uppos>y)return true; return false;
}
void work()  //Main process
{
    for(i=1;i<=n;i++) for(j=1;j<=m;j++)    for(k=1;k<=m;k++)
    if(check(i,j)&&check(i-1,k)) if(j!=m)  //Not on the pipeline
    {
        if(k-down[i-1]==j)f[i][j]=min(f[i][j],f[i-1][k]);  //Fall off
        if(j>k&&(j-k)%up[i-1]==0)f[i][j]=min(f[i][j],f[i-1][k]+(j-k)/up[i-1]);  //Jump up
    }
    else  //j=m special judgment
    {
        if(k==m&&down[i-1]==0)f[i][j]=min(f[i][j],f[i-1][k]);
        else if(k==m&&down[i-1]!=0)f[i][j]=min(f[i][j],f[i-1][k]+1);
        else {if((j-k)%up[i-1]==0)f[i][j]=min(f[i][j],f[i-1][k]+(j-k)/up[i-1]);
        else f[i][j]=min(f[i][j],f[i-1][k]+(j-k)/up[i-1]+1);}
    }
}
int findpipe(int num)  //There are several pipes from 0 to num-1
{
    int tot=0; for(k=0;k<num;k++) if(p[k].uppos!=m+1)tot++; return tot;
}
void find()  //Find the answer
{
    bool flag; int minimum=1000000000; for(i=1;i<=n;i++)
    {
        flag=false; for(j=1;j<=m;j++)flag|=f[i][j]<10000000;
        if(!flag){cout<<0<<endl; cout<<findpipe(i)<<endl; break;}
    }
    if(flag) {for(j=1;j<=m;j++)minimum=min(minimum,f[n][j]);
    cout<<1<<endl; cout<<minimum<<endl;}
}
int main()
{
    memset(f,sizeof(f),10000000); readdata(); work(); find(); return 0;
}

Full Score code

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int M=10005,N=1005,Inf=0x3f3f3f3f;
int topp[M],endd[M],have[M];
int dp[M][N];
int up[M],down[M];
int n,m,k,maxx;
int main()
{
    scanf("%d%d%d",&n,&m,&k);
    for(int i=0;i<n;i++) scanf("%d%d",&up[i],&down[i]);
    for(int i=0;i<=n;i++) topp[i]=m+1;
    for(int i=1;i<=k;i++){
        int x;scanf("%d",&x);
        scanf("%d%d",&endd[x],&topp[x]);have[x]=1;   //Record whether there is a pipe or not
    }
    for(int i=1;i<=n;i++)
     for(int j=0;j<=m;j++)
      dp[i][j]=Inf;
    dp[0][0]=Inf; //Initialization

    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)//Rise
        {
            if(j>up[i-1])
            {
                dp[i][j]=min(dp[i][j],dp[i-1][j-up[i-1]]+1);    
                dp[i][j]=min(dp[i][j],dp[i][j-up[i-1]]+1);
            }
            if(j==m)//Special judgement
            {
                for(int d=m-up[i-1];d<=m;d++)
                {
                    dp[i][j]=min(dp[i][j],dp[i-1][d]+1);    
                    dp[i][j]=min(dp[i][j],dp[i][d]+1);
                }
            }
        }

        for(int j=endd[i]+1;j<=topp[i]-1;j++)//decline
        { 
            if(j+down[i-1]<=m)
             dp[i][j]=min(dp[i][j],dp[i-1][j+down[i-1]]);
        }
        for(int j=1;j<=endd[i];j++) dp[i][j]=Inf;
        for(int j=topp[i];j<=m;j++) dp[i][j]=Inf;
    }
    int ans=Inf,tot=k;  //Find the answer
    for(int i=n;i>=1;i--)
    {
        for(int j=endd[i]+1;j<=topp[i]-1;j++) 
        ans=min(ans,dp[i][j]);
        if(ans!=Inf) break;
        if(have[i]) tot--;
    }
    if(tot==k) printf("1\n%d\n",ans);
    else printf("0\n%d\n",tot);
    return 0;
}