sort

How to analyze a "sorting algorithm"?

1. Execution efficiency of sorting algorithm
   1.1 time complexity of best case, worst case and average case
   1.2 coefficient, constant and low order of time complexity
   1.3 comparison times and exchange (or movement) times
2. Memory consumption of sorting algorithm
3. Stability of sorting algorithm

Why investigate the stability of sorting algorithm?
A: in real software development, what we need to sort is often not a simple integer, but a group of objects. We need to sort according to a key of the object. For example, there are two attributes: order time and commodity price. If you need to ensure the order time within the same price after sorting the price, you need a stable sorting algorithm.

Bubble sorting

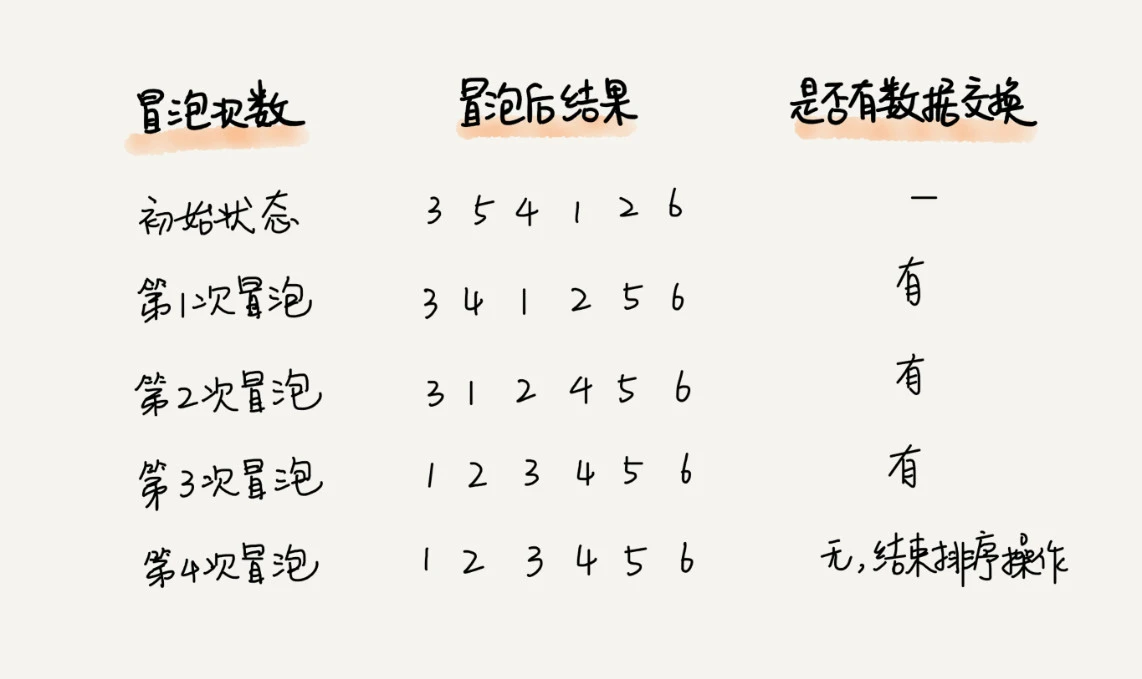
Fake sort code
isOrderly is used to end the sorting ahead of time when the array is found to be ordered

static void bubbleSort(int[] arr){
        int len=arr.length;
        for(int i=0;i<len;i++){
            boolean isOrderly=true;
            for(int j=0;j<len-i-1;j++){
                if(arr[j]>arr[j+1]){
                    isOrderly=false;
                    int tmp=arr[j];
                    arr[j]=arr[j+1];
                    arr[j+1]=tmp;
                }
            }
            if(isOrderly){ break; }
        }
    }

Algorithm analysis:
1. Spatial complexity: only exchange operation and several temporary variables, i.e. O(1)
2. Stability: when two adjacent numbers in the code are equal, they will not be exchanged, maintaining stability
3. Time complexity:
Best case O(n) (at least one traversal)
Worst case O(n^2) (pure reverse order)

Here, the author introduces a method to analyze the average time complexity: using reverse order numbers and ordinal numbers
Reverse order pair: a [i] > = a [J] and I < J, then it is called a reverse order pair here
Reverse order number: the number of reverse order pairs in the array. The same is true for ordered pairs
We can also get a formula: reverse order degree = full order degree - order degree. Our sorting process is a process of increasing the degree of order, reducing the degree of reverse order, and finally reaching the full degree of order,

Insert sort

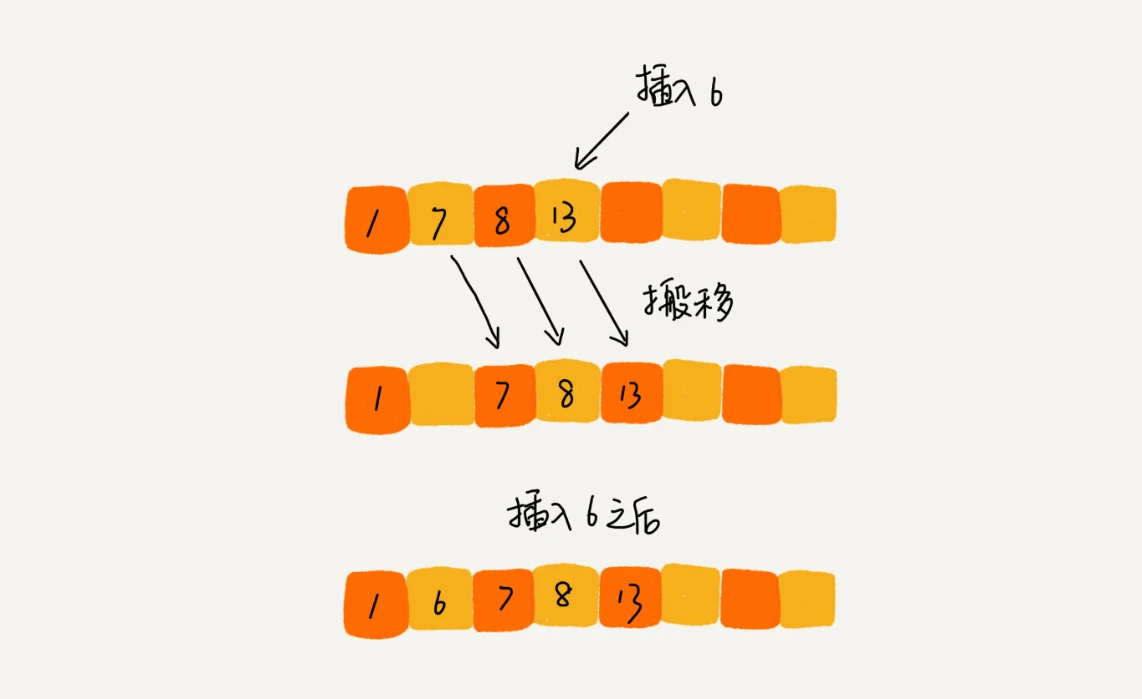
Idea: divide the data in the array into two intervals, sorted interval and unordered interval. Take the elements in the unordered interval, find the appropriate insertion position in the sorted interval, insert them, and ensure that the data in the sorted interval is always in order. Repeat this process until the element in the unordered interval is empty and the algorithm ends.

static void insertionSort(int[] arr){
        int len=arr.length;
        for(int i=1;i<len;i++){
            int temp=arr[i];
            int j=i-1;
            for(;j>=0;j--){
                if(arr[j]<=temp){
                    break;
                }
                arr[j+1]=arr[j];
            }
            //Note that it must be written outside, not before break
            arr[j+1]=temp;
        }
    }

Algorithm analysis:
1. Space complexity: O(1)
2. Stability: for elements with the same value, we can choose to insert the following elements into the back of the previous elements, so as to keep the original sequence unchanged. Therefore, insertion sorting is a stable sorting algorithm.
3. Time complexity: best O(n), worst and average O(n^2)

Select sort

It also divides the array into ordered and unordered parts, but each time, the most value is selected from the unordered and placed at the end of the ordered part. However, because this "put" is actually an exchange operation, the selection sorting is not stable

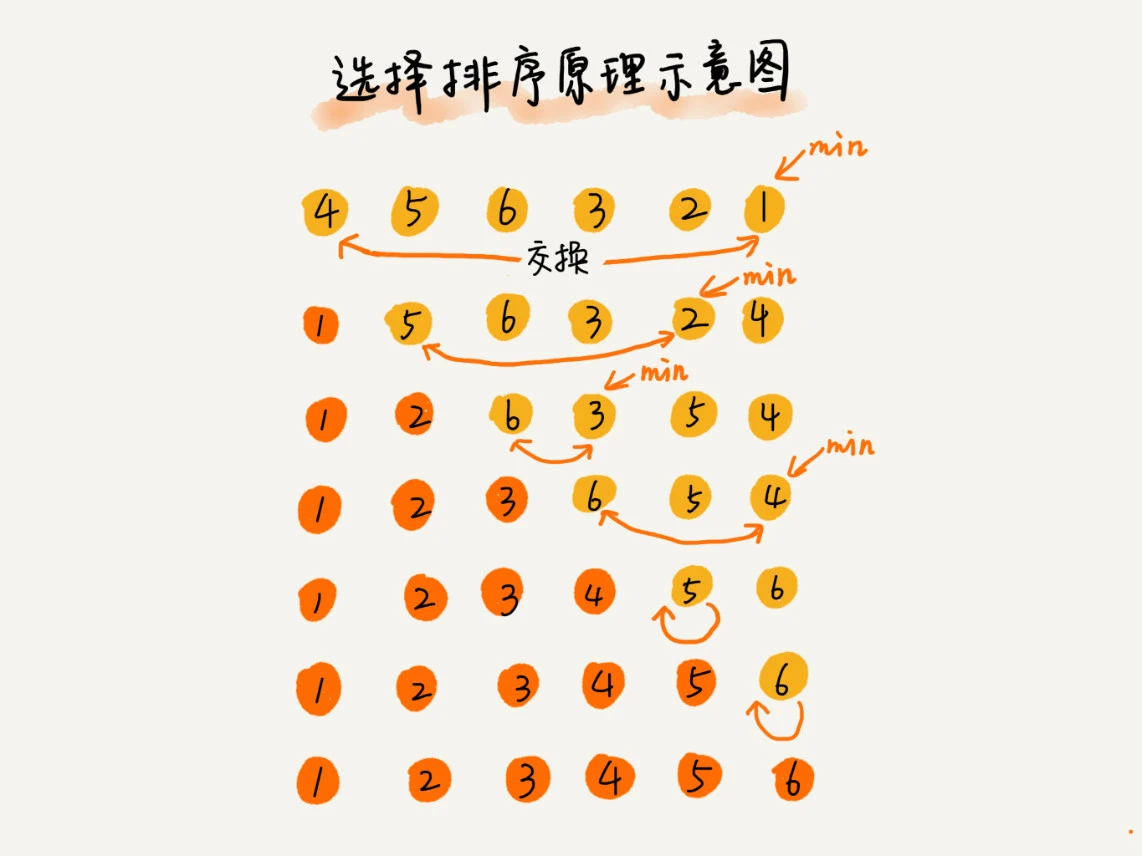
static void selectionSort(int[] arr){
  	int len=arr.length;
    for(int i=0;i<len-1;i++){
        int min=Integer.MAX_VALUE;
        int tag=i;
        //Get the minimum value of the unordered part
        for(int j=i;j<len;j++){
            if(min>arr[j]){
                min=arr[j];
                tag=j;
            }
        }
        if(tag!=i){
            int temp=arr[tag];
            arr[tag]=arr[i];
            arr[i]=temp;
        }
    }
}

Algorithm analysis:
1. Space complexity: O(1)
2. Stability: unstable
3. Time complexity: best O(n), worst and average O(n^2)

Here the author also said

We roughly count the time of executing an assignment statement as unit_time, and then use bubble sort and insert sort to sort the array with the same reverse order degree of K. Bubble sorting requires K exchange operations and 3 assignment statements each time, so the total time of exchange operation is 3*K unit time. The data movement operation in insertion sorting only needs K unit time.
This is just our very theoretical analysis. For the experiment, for the above Java code of bubble sorting and insertion sorting, I wrote a performance comparison test program, randomly generate 10000 arrays, each array contains 200 data, and then sort them with bubble sorting and insertion sorting algorithms on my machine. The bubble sorting algorithm can be executed in about 700ms, The insertion sorting only takes about 100ms!
Therefore, although bubble sort and insert sort have the same time complexity, both of which are O(n2), if we want to optimize the performance to the extreme, insert sort must be the first choice.

Then turn out the Hill sort I wrote before (it can be regarded as the optimization of insertion sort)
Spatial complexity O(1), average time complexity O(nlogn)
The following is a demo I copied from someone else's blog

void ShellSort(int N,int *a)
{
	int gap,temp;
	int i,j;
	for(gap=N/2;gap>0;gap/=2)
	{
		for(i=gap+1;i<=N;i++)
		{
			temp=a[i];
			for(j=i-gap;j>=0&&a[j]>temp;j-=gap)
			{
				a[j+gap]=a[j];
			}
			a[j+gap]=temp;
		}
	}
}