Number Number Number

In python's documentation, there are several points to note:

• The Math module does not support functions of complex numbers, which are calculated using cmath.So most of them don't support complex numbers.
• Under the math module, floating-point numbers are returned unless the label is displayed.

number Definition

• number is used to define data, and data is not allowed to change.Only memory space can be reclaimed.number is immutable data.str is also immutable data.
• Variables are created when they are assigned
• Delete the variable del var1,varr2, you can delete more than one at the same time, will delete memory space, subsequent use will not define

value type

• Integer (int): No decimal point, can be positive or negative, or can be expressed in hexadecimal, octal, binary integers
• Floating-point type: Integer and decimal components, which can be scientific counting
• Complex: The real and imaginary parts of a complex number are floating point numbers.a+bj or complex(a,b)

# 28-hexadecimal represents integer of type int
print(0xA0f)#2527
print(type(0xA0f))#<class int>
print(type(0o37))# int
print(type(0b 10))#int

Binary Representation

Binary: 0b
Octal: 0o
Hexadecimal: 0x

int range/float range, etc.

1. The value range of int is -231 ~ 231-1, i.e. -2147483648 - 2147483647. int occupies 4 bytes, 8 bits per byte, or 32 bits.Each int data can be represented in 32-bit binary. Detailed range of int s The link goes into more detail.
2. float range, Baidu out of the attitude answer, but also need to find a supplement again

Number Type Conversion

• Ability to convert various data types using functions
• int(x): converted to an integer
• float(x): converted to floating point number
• complex(x): converts to a complex number, the imaginary part is 0
• complex(x,y): converted to complex x+yj

int(x) transformation definition

• int(x), comes in two forms.int(x) is converted to decimal by default, and int(x,base) to base.
• The int conversion returns an int type.
• int() =0
• int(x, base) converts numbers and strings to int type; if x is a number, use
  x.int(); if x is not a number and a second parameter is given, the type of the first parameter should be string, byte, byte array
• base has a default value of 10 and a range of 0, 2-36; 0 represents the conversion to decimal.

class int(object)
 |  int(x=0) -> integer  # Return is of type int
 |  int(x, base=10) -> integer #Return is of type int
 |  Convert a number or string to an integer, or return 0 if no arguments are given.  If x is a number, return x.__int__().  For floating point numbers, this truncates towards zero.
 # int(x) converts numbers and strings to int type and returns 0 if no parameter int() is given
 #If x is a number, X. u int_() 
 |  If x is not a number or if base is given, then x must be a string,  bytes, or bytearray instance representing an integer literal in the given base.  The literal can be preceded by '+' or '-' and be surrounded by whitespace.  The base defaults to 10.  Valid bases are 0 and 2-36.
 # int (x, base) If x is not a number and is based on the second parameter, the first parameter is a string, byte, byte array, representing integer text in a given cardinality.Parameters can be integers or negative numbers, binary numbers are decimal by default, and the value orientation is 2-36.
 |  Base 0 means to interpret the base from the string as an integer literal. # base=0 means to convert a string to a decimal integer
 |  >>> int('0b100', base=0)
 |  4

int(x) example

• int() rounding, not rounding, is the direct discarding of decimal parts.That is, rounding to zero
• Complex cannot be cast to int type, complex is a floating point number, but cannot be cast to floating point can't convert complex to float/int
• Int() can only convert a string of pure numbers to an integer, meaning it does not convert a string of decimals, or it will not convert to ASCII code if invalid literal for int() with base 10:'12.3'.
• Binary consists of only 0,1, or binary encoding.
• If you want to do binary conversion, that is, when you have the second parameter, x must be a string, byte, byte array or else you will get an error Oh TypeError: int() can't convert non-string with explicit base type error, you cannot convert data of non-string type.
• If you want to convert the corresponding binary, the representation should correspond to the binary, that is, 0x12 is represented in 8-digit, which is an error!Binary type should correspond to format
• You can convert bool, True=1;False=0; note that capitalization is not a variable!
• 0b 0o 0x corresponds to binary, octal, and hexadecimal respectively. It must be used with the base parameter, otherwise it will be a person string, the base range is 0~36
• print(int('1'*2,2)) pays attention to repeated output of strings, repeating before converting.
• Cannot convert Roman characters, unicode characters or
• If there are numbers and letters, error will occur, 11a does not have the same implicit conversion as js

#print(help(int))
print(int())#0
print(int(2))#2
print(int(2.1))#2
print(int(-2.1))#-2
print(int(2.6))#2
#print(int(1+2j)) can;t convert complex to int
#print(float(1+2j))

#character
print(int('15'))#15
#print(int('12.3')) #invalid literal for int() with base 10: '12.3'
#print(int('s'))
#print(int(12,8))TypeError: int() can't convert non-string with explicit base
print(int('12',8))#10
print(int('121',8))#81
#print(int('0x12'))#ValueError: invalid literal for int() with base 10: '0x12'
# This is mistaken for a character and must be brought into production
print(int('0x12',16))#18
#print(int('0x12',8))# Binary type should correspond to
print(int('0o12',8))#10
print(int('0b11',2))#3
#print(int([0b10,0b11,0b01],2)) typearray??
#print(int(b'\x01\x02\x03')) does not understand need to be supplemented
# Various Binary
print(int('12',3))#5
print(int('1234',36))#49360
print(int(True))#1
print(int(False))#0
# Note that the string *represents multiple outputs
print(int('1'*2,2)) # Converts 2 under binary to corresponding 10
#11=3
#Convert to decimal in the case of x-ary
print(int('1'*3,2)) #Represents a total of 3 bits  
#(111) = 1*2 square + 1*2 power + 1*2 zero power

print(int('1'*64,2)) 
#Represents a total of 64 1 and adds them to the second power multiplied by 2

print(int('three')) # Cannot convert Roman characters Hahaha

float(x) conversion definition

• float(x) returns a floating point number
• Decimal points are precise, they are ignored when they exceed the computer's precision and only read the previous numbers
• Complex numbers cannot be converted to floating point numbers
• float has only one parameter and no binary conversion function.
• Cannot convert Roman characters, etc.It is also not possible to convert letters using ASCII codes
• There is no implicit conversion 12q can't convert string to flaot like js

class float(object)
 |  float(x) -> floating point number
 |  #Return floating point number
 |  Convert a string or number to a floating point number, if possible.
 # Convert String, Number to Floating Point
 #

float(x) example

#print(help(float))
print(float(1))#1.0
print(float(-2.1))#-2.1
#print(float(1+2j)) can't conver complex to float
#print(float('12',8))
print(float('12.1'))#12.1 int can't
#print(float('0o12')) could not convert string to float
#print(float('three'))
#print(float('12a'))
print(float(True))#1.0
print(float(False))#0.0

complex(x,y) definition

• Returns a complex number in two forms.x is the real part, y is the imaginary part, and is a floating point number; in either case, it returns a complex number.
• complex(x):x is a number, y is 0 by default, output form x+0j
• complex(x,y): output form x+yj
• Decimals and integers can be used as real and imaginary parts, string-type data can also be used; string types are converted to floating-point numbers.No implicit conversion exists for strings.
• If the first parameter is a string type number, then there cannot be a second parameter can;t take second arg if first is a string; when string data is the first parameter, it can be a pure real number or a complex number, i.e.'a+bj'
• complex(a,b) = a+b*j, and finally returns the data.j*j = -1 child: print (complex (1,2j)#-1+0j J = 1+2j*j = 1-2 = -1

class complex(object)
 |  complex(real[, imag]) -> complex number
 |  #Return complex numbers
 |  Create a complex number from a real part and an optional imaginary part.
 # Create a negative number with a real part and an optional imaginary part
 |  This is equivalent to (real + imag*1j) where imag defaults to 0.
 # This is equivalent to the imaginary part defaulting to 0
 

complex(x) example

Insert Generation Here#print(help(complex))
print(complex(1))#1+0j
print(complex(1,1.1)) #(1+1.1j)
print(complex('1.1'))# Strings that are pure numbers are converted to float types
print(complex('1.1+2j'))#1.1+2j
#print(complex('1.1',2))#can't take second arg if first is a string
print(complex('2'))#2+0j
#print(complex('2q')) value error
print(complex(1,2j))#-1+0jj =  1+2j*j = 1-2 = -1
print(complex(1+2,2j)) # 3-2 = 1+0j
#Chips

Data type in operation

• The real part and the imaginary part of a complex number are floating point numbers
• Floating-point operations on different machines have different results, depending on accuracy, /returns floating-point numbers, //gets data depending on the type of data, but any calculation involving floating-point numbers returns floating-point numbers.
• Integers are converted to floating-point numbers when mixed with different types of numbers

Numeric function - math.ceil() returns an integer greater than or equal to

• Math.ceil definition, which is a Math function, requires math.ceil(x) when it is written; returns an integer greater than or equal to import math when it is used

ceil(x)
Return the ceiling of x, the smallest integer greater than or equal to x. If x is not a float, delegates to x.__ceil__(), which should return an Integral value.
#Returns the upper limit of X (ceiling), an integer greater than or equal to X.If x is not a floating point number, then using the X. u ceil_() method requires an integer to be returned

• Complex numbers and strings cannot be used
• ceil means the ceiling and returns an integer greater than or equal to.

import math
print(math.ceil(1))#1
print(math.ceil(2.1))#3
print(math.ceil(2.5))#3
# Not rounded
print(math.ceil(-0.1))#0
print(math.ceil(-1.1))#-1
#print(math.ceil('2')) # must be real number not str
#print(math.ceil(1+2j))# cnat' conver complex to float
#print(math.ceil((1+2j)))# can't

Numeric Function - math.exp() Exponential to x

• math.exp Definition: Returns the ex index

Return e**x  # Return e**x

• import math needs to be imported to invoke methods through static objects
• The x parameter cannot be a string, a complex number, or an int and float type.

#exp
print(math.exp(2))
print(math.exp(2.1))
#print(math.exp('12')) must be real number not str
#print(math.exp(1+2j))can't convert complex to float
print(math.exp(-2))

Mathematical function--math.fabs() for absolute values

• math.fabs(x) definition, import math required

math.fabs(x)
Return the absolute value of x. # Returns the absolute value of x

• All returned are floating point numbers, valid only for int, float types, complex numbers, strings

# fabs
print(math.fabs(1))#1.0 #
print(math.fabs(1.1))#1.1
print(math.fabs(-1.2))#1.2
#print(math.fabs('12.1'))# must be rral number not str
#print(math.fabs(1+2j))can't convert complex to float

Differences between math.fabs and abs

abs() is a built-in function.The fabs() function is defined in the math module.

• The fabs() function is only valid for floating-point and integer values.All returned are floating point numbers
• abs() can also be used in complex numbers.Return based on actual data

Math Function - math.floor returns integers less than or equal to

• math.floor definition, returns an integer less than or equal to, requires import math

Return the floor of x, the largest integer less than or equal to x. If x is not a float, delegates to x.__floor__(), which should return an Integral value.
# Returns an integer that is the smallest or equal to X. If x is not a floating point number and X. u floor_u, it should return a floating point number, that is, a string can be used?

• Floor means floor and returns an integer less than or equal to; there is no rounding
• Cannot use complex numbers, strings, only int, flaot

# floor
print(math.floor(1.1))#1
print(math.floor(2.7))#2
print(math.floor(-3.5))#-4
print(math.floor(-0.1))#-1
#print(math.floor('12'))#must be ral number not str
#print(math.floor(1+2j))# can't convert complex to float

Numeric function - math.modf(x) returns the fractional and integer parts of a floating point number

• math.modf(x) definition, a math function, requires import math
• Returns the integer and decimal portions of x, all returned as floating-point numbers, with symbols.
• Can't string numbers oh

Return the fractional and integer parts of x. Both results carry the sign of x and are floats.
#Returns the fractional and integer parts of x, both of which are symbolized with X and are floating point types.

#modf
print('modf')
print(math.modf(1))# 0.0 1.0
print(math.modf(2.1))# 0.1 18 Bit 2.0
print(math.modf(-1.3))# -0.3000000...  -1.0
#print(math.modf('1.1')) must be real number
#print(math.modf(1+2j)) #cmath

Math Function - math.copysign(x,y) x Gets the symbol of Y

• math.copysign(x,y) definition: Returns the number of x, the symbol is determined by y.
• All returned are floating point numbers
• Results for 0, 0.0, -0, -0.0 may be different on different platforms

Return a float with the magnitude (absolute value) of x but the sign of y. On platforms that support signed zeros, copysign(1.0, -0.0) returns -1.0.
#Returns x with size, but the sign of X depends on y.Support data is 0,

#math.copysign
print(math.copysign(1,2))#1.0
print(math.copysign(2,-23))#-2.0
#print(math.copysign(2,1+2j)) complex cant
#print(math.copysign(1,'23')) not str

Numeric function - math.factorial(x) factorial

• math.factorial(x), returns the factorial of 1-x, x cannot be negative and floating point numbers, only integers

Return x factorial. Raises ValueError if x is not integral or is negative.
#Returns the factorial of X and errors valueError if x is not of type int and negative

print(math.factorial(3))#6
print(math.factorial(4))#24
print(math.factorial(2.0))# Equals 2
#print(math.factorial(2.3))# not can only be an integer

Numerical function-math.fmod(x,y) modulus complement

• math.fmod(x,y) definition: Ability to redundantly model data, mainly floating point numbers.import math is required and returns a floating point number.
• %Remaining floating-point numbers is not accurate, so fmod is used to calculate floating-point numbers.% for integers
• math.fmod (x,y) differs from%
  (1) math.fmod returns floating-point numbers,%is returned from the data, and if they are all of type int, returns type int, and if one of the data is a floating-point number, returns a floating-point number.
  (2) the sign (+/-) of math.fmod(x,y) result is the same as x;%sign is the same as y.And the same data (negative numbers) are different in calculation.As shown below
  (3) math.fmod(x,y) is calculated as |x|%|y|;
  %: If the x, y symbols (+/-) are the same, the result |x|% |y|
  If the x,y symbols are different, the result is |y| - (|x|% |y|)
  Note, however, that when x and y are different, |y| - (|x|% |y|), the following two conditions need to be met:
  1. |x| is much smaller than |y|;
  2. At least one of X and Y is a floating point number (only floating points cause loss of precision).At this point, the resulting (|x|% |y|) value is relatively small (i.e., equal to |x|), but because |y| is relatively large and the computer loses precision in floating point calculations, the final result of'|y| - (|x|% |y|)) is truncated to a strange phenomenon of'|y|', as shown below.
  Here's an example!

# fmod
print(1%2)#1
print(10%3)#1
print(10.1%3)#1.099999999999..6
print(math.fmod(10,3))#1
print(math.fmod(10.1,3))#1.09999..6
print(math.fmod(100.02,2))
print(math.fmod(-100.01,3))#-1.01000...
print(math.fmod(100.01,-3))#1.01...The symbol is related to x
print(-100.01 %3)#1.98
print(100.01%-3)#-1.98
# 100.3 % 3   -100.3%3  100.3%-3  -100.3%-3
print(math.fmod(100.3,3)) #1.299...72
print(100.3%3) #1. 299...72
#The results are the same
print(math.fmod(-100.3,3)) 
# -(|-100.3|% |3|)=-1.2999 equals approximately 1.3 Symbol x prevails
print(-100.3%3)
# Symbols differ in positive and negative based on y|y| - (|x|% |y|) = 3-1.2999 =1.7..


# Example reload, not tested.
print('"%"Exceptions to modulo operators:     -0.0000000001 % 10000000 =', 
      -0.0000000001 % 10000000, '(Is equivalent to the result directly equal to the second number)')
# Using fmod to model does not happen
print('Use fmod Modeling, normal: math.fmod(-0.0000000001, 10000000) = ', 
      math.fmod(-0.0000000001, 10000000), '(The result is equal to the first number)')
print('"%"Exceptions to modulo operators: 10   % -10000000000000000000000.0 =', 
      10 % -10000000000000000000000.0, '(Is equivalent to the result directly equal to the second number)')
print('"%"Exceptions to modulo operators:-10.0 %  10000000000000000000000   =', 
      -10.0 % 10000000000000000000000, '(Is equivalent to the result directly equal to the second number)')
#This is not true for non-floating point numbers:
print('"%"Modulo operator, normal:    10    % -10000000000000000000000   =', 10 % -10000000000000000000000)
print('"%"Modulo operator, normal: , -10    %  10000000000000000000000   =', -10 % 10000000000000000000000)

Portability of Numeric Functions - math.frexp(x)/math.ldexp(x,i) Floating Point

• math.frexp(x) definition, x = m * 2e; find m,e from x, return the ancestor (m,e), m range: 0.5 <= abs(m) < 1, m is a floating point number, e is an integer; make the floating point number split
• Math.frexp(x) splits floating point x into (m,e) ancestors, which can then be merged using ldexp.
• math.ldexp(x,i) is the inverse operation of math.frexp(x).Returns a floating point number.

Return the mantissa and exponent of x as the pair (m, e). 
#Returns the tail and exponent of x as a pairing (m, e).
m is a float and e is an integer such that x == m * 2**e exactly.
# M is a floating point number, e is an integer, x == m *(2**e)
 If x is zero, returns (0.0, 0), otherwise 0.5 <= abs(m) < 1. This is used to "pick apart" the internal representation of a float in a portable way.
 # A portable way to represent a floating point number is to split a floating point number into exponential forms.
 # If x is 0, return (0.0, 0); repeat

print(math.frexp(10)) #x = m * 2 **e (0.625,4)
print (math.frexp(100)) # 0.71825 ,7
print(math.frexp(10.2))
#print(math.frexp('12')) not str complex
 print(math.ldexp(0.625,4))#10.0

Numeric Functions - Accumulation of math.fsum(iterable) iterators

• The math.fsum(iterable) parameter is iterative; returns the sum in iterative data.Iterative: string, dictionary, meta-ancestor, list; import math introduced
• Parameters must be iterative and cannot print(math.fsum(1,2,3,4)) TypeError: fsum() takes exactly one argument (4 given); cannot be strings, nor arrays of string types, and have no implicit conversion
• All returned are floating point numbers
• math.fsum is more accurate than sum

Return an accurate floating point sum of values in the iterable. Avoids loss of precision by tracking multiple intermediate partial sums:
# Returns an exact floating point value.By tracking multiple intermediate parts and avoiding loss of precision.
>>>
>>> sum([.1, .1, .1, .1, .1, .1, .1, .1, .1, .1])
0.9999999999999999
>>> fsum([.1, .1, .1, .1, .1, .1, .1, .1, .1, .1])
1.0 # More precise

# fsum(iterable)
#print(math.fsum(1,2,3,4)) TypeError: fsum() takes exactly one argument (4 given)
#print(sum(1,2,3,4)) typeError at most 2 arguments
print(math.fsum((1,2,3,4)))#10.0
#print(math.fsum(('1','2','3','4'))) must be real number not str
print(math.fsum([1,2,3,4,5]))#15.0
print(math.fsum([.1, .1, .1, .1, .1, .1, .1, .1, .1, .1]))#1.0
print(sum([.1, .1, .1, .1, .1, .1, .1, .1, .1, .1]))#0.99999

math.gcd(a,b) for the greatest common divisor

• math.gcd(a,b) definition, find the greatest common divisor of a, d, return int type, a, d need to be integer
• math.gac(0,0) = 0

Return the greatest common divisor of the integers a and b. # Gcd
If either a or b is nonzero, then the value of gcd(a, b) is the largest positive integer that divides both a and b. gcd(0, 0) returns 0.
#If either a or B is non-zero, then the value of gcd(a, b) is the largest positive integer divided by a and B at the same time.gcd(0,0) returns 0

print(math.gcd(12,3))#3
#print(math.gcd(12.2,3)) TypeError: 'float' object cannot be interpreted as an integer
#print(math.gcd(12,'12')) str can't 

Numeric functions - math.isclose(a, b, *, rel_tol=1e-09, abs_tol=0.0) a, B data approximation

• math.isclose() definition: Compare whether two parameters a and b are close or not.
• Algorithms: abs(a-b) <= Max (rel_tol * Max (abs(a), abs(b)), abs_tol).
• NaN is not close to any number, inf, -inf is infinitely close to itself
• rel_tol: Relative tolerance, the maximum difference that can exist between ab s.The default is 1e-9, making sure that at least nine little trees are the same.
• abs_tol: Absolute tolerance, which is the smallest difference that can exist between ab s, is infinitely close to zero.
• When using, note the format, you must rel_tol =...abs_tol.Otherwise error print (math.isclose (0.1,0.01, rel_tol=1)#true
• I don't know what it means, late supplement

Return True if the values a and b are close to each other and False otherwise.
#  If a and b are close together, return True, otherwise return false

Whether or not two values are considered close is determined according to given absolute and relative tolerances.
#The proximity of two values depends on the absolute and relative tolerances given, namely abs_tol and rel_tol

rel_tol is the relative tolerance – it is the maximum allowed difference between a and b, relative to the larger absolute value of a or b. For example, to set a tolerance of 5%, pass rel_tol=0.05. The default tolerance is 1e-09, which assures that the two values are the same within about 9 decimal digits. rel_tol must be greater than zero.
# Relative tolerance This is the maximum allowable difference between a and b, relative to the larger absolute value of a or b, for example, to set the tolerance to 5%, pass rel_tol=0.05.The rel_tol default value is 1e-09, which ensures that the two values are the same within about 9 decimal places.Rel_tol must be greater than 0

abs_tol is the minimum absolute tolerance – useful for comparisons near zero. abs_tol must be at least zero.
# Absolute tolerance: abs_tol is the minimum absolute tolerance - useful for near-zero comparisons.Abs_tol must be at least zero.
If no errors occur, the result will be: abs(a-b) <= max(rel_tol * max(abs(a), abs(b)), abs_tol).
#If no error occurs, the result will be: abs(a-b) <= Max (rel_tol * Max (abs(a), abs(b)), abs_tol).
the IEEE 754 special values of NaN, inf, and -inf will be handled according to IEEE rules. Specifically, NaN is not considered close to any other value, including NaN. inf and -inf are only considered close to themselves.
#NaN is not considered close to any other value, including NaN.Inf and-inf are only considered close to themselves.

print(math.isclose(0.1,0.01)) #false 9 identical
#print(math.isclose(0.1,0.01,0.1))# Up to two locations???
print(math.isclose(0.1,0.01,rel_tol=0.1))#false
print(math.isclose(0.1,0.01,rel_tol=1))#true

Is the numeric function math.isfinite(x) finite

• Definition of math.isfinite(x): To determine if a number is finite, a finite number returns true, an infinite number returns false

Return True if x is neither an infinity nor a NaN, and False otherwise. (Note that 0.0 is considered finite.)
# Returns True if x is infinite and non-numeric returns false.Note that 0.0 is considered Limited

• Returns bool type
• NaN, positive infinity, negative infinity are infinite, returning false

Numeric function - math.isinf(x) is infinite

• math.inf(x) defines that x is positive infinity, negative infinity returns true, and infinite number returns true
• Returns bool type

Return True if x is a positive or negative infinity, and False otherwise.
# Returns true if x is positive and negative infinity, false otherwise

print(math.isinf(12))#false
# not str complex

Numeric function - math.isnan(x) is not numeric

• math.isnan(x) definition: Place back true if x is not a number, or false if x is not.

Return True if x is a NaN (not a number), and False otherwise.
But it can't be a string either

Numeric function - math.trunc(x) returns the integer part of floating point number x

• math.trunc(x): Returns the integer portion of x, modf outputs integer decimal numbers as a tuple., which returns the type of int

Return the Real value x truncated to an Integral (usually an integer). Delegates to x.__trunc__().
#Returns the real value x truncated to an integer.Represents X. u trunc_ ().

Insert the code snippet print (math.trunc(2)#2 here
print(math.trunc(2.3))#2
print(math.trunc(4.34))#4 ```

Numeric Function - math.log(x,[base])

• math.log(x,[base]), definition., need import math

With one argument, return the natural logarithm of x (to base e).
# A parameter that returns the base e logarithm
With two arguments, return the logarithm of x to the given base, calculated as log(x)/log(base).
# Two parameters, will be defined based on the base data

• In the calculation, the value needs to conform to the interval range (a > 0, and a is not equal to 1) Error: ValueError: math domain error
• All returned are floating point numbers
• There are two parameters, log(x) and log(x, [base]), with base as the base and base as the default;
• Log (x, e) is not allowed and E is considered a variable
• Base > 0 and not equal to 1, related to the interval of logarithm

#log
print(math.log(2))
#print(math.log(-1)) interval error
print(math.log(2.3))
print(math.log(2,2))#1.0
#print(math.log(2,e))# Cannot e
print(math.log(2,10))
print(math.log(2,3))

Numeric Functions - math.log10(x)/math.log2(x)

• math.log10(x), need to import math, base 10
• Math.log2(x), 2 is bottom

Return the base-10 logarithm of x. This is usually more accurate than log(x, 10). 
# Base is base 10, equal to log(x,10)

• Returns a floating point number.
• Same functionality as math.log(x,10)

print(math.log10(100))#2.0  lg100
print(math.log2(100)) #log2100

Numeric Function - math.log1p(x)

• math.log1p(x) = =ln(1+x), which is the base e calculation.

Return the natural logarithm of 1+x (base e). The result is calculated in a way which is accurate for x near zero.

Numeric Functions - math.pow(x,y)/pow(x,y,[z])

• math.pow(x,y) definition, requires import math, returns floating point numbers
• pow(x,y[z]) is a built-in function and does not require the introduction of math modules.The data type returned is related to x, y. When x, y are all of type int, return the type int, depending on the specific situation.
• pow(1.0,x) or pow(x,0.0), whether x is 0 or NaN output is 1.0;
• In math.pow(x,y),x is negative
• Parameters must be numeric, not other types, such as string numbers, complex numbers, not convertible, using cmath.
• math.pow(x,y), when x > 0, y cannot be a decimal, it must be an integer, otherwise it prompts valueError, not within the scope of the defined field.This is not very understood, but the pow built-in function can be calculated.
• pow(x,y,z) z is a remainder operation equal to x**y%z
• 2.0 equals 2, the rest is the same, so be careful when calculating

Return x raised to the power y. Exceptional cases follow Annex 'F' of the C99 standard as far as possible. In particular, pow(1.0, x) and pow(x, 0.0) always return 1.0, even when x is a zero or a NaN. If both x and y are finite, x is negative, and y is not an integer then pow(x, y) is undefined, and raises ValueError.
# Returns the y-th power of x.Exceptions follow Annex F of the C99 standard whenever possible.
#In particular, pow(1.0, x) and pow(x, 0.0) always return 1.0, whether x is 0 or NaN, or floating point numbers
#If X and y are finite, then x is negative and Y is not an integer, then pow(x, y) is undefined and produces a ValueError.

Unlike the built-in ** operator, math.pow() converts both its arguments to type float. Use ** or the built-in pow() function for computing exact integer powers.
#Unlike the built-in ** operator.The POW converts both parameters to floating point numbers.Use **/pow to calculate integer power

#pow  math.pow
print(math.pow(1,2))#1.01
print(pow(1,2))#1
print(pow(1.1,1.1))#1.11...
print(math.pow(1.0,1))#1.0
print(math.pow(-2,-1))#-0.5
#print(math.pow(-3,-2.2)) valueError math domain error value range error
print(pow(-2,-1.2))# What?Built-in functions can return complex numbers
print(math.pow(-2.2,1))#-2.2
print(pow(1,2,3))#1**2%3

Numeric function math.sqrt()

• math.sqrt(x) definition, returns the square root of x, requires import math
• All returned are floating point numbers
• Negative numbers have no square root. valueError:math domain error is known by the defined domain
• math.sqrt(0) = 0

math.sqrt(x)
Return the square root of x.

# sqrt
print('sqrt')
print(math.sqrt(1))#1.0
print(math.sqrt(1.1))
print(math.sqrt(23.23))#4.8
#print(math.sqrt(-123))# math.domain error
#print(math.sqrt('12')) not str

Math Function - math.exp(x)

• math.exp(x) definition: calculates the answer to ex.
• Example: math.exp(2)

Math Function - math.expm1(x)

• Define math.expm1(x) to calculate ex-1, which is more accurate than math.exp(x)-1 and reduces the loss of precision.
• Loss of precision is only shown under large numbers

Return e**x - 1. For small floats x, the subtraction in exp(x) - 1 can result in a significant loss of precision; the expm1() function provides a way to compute this quantity to full precision:
>>>
>>> from math import exp, expm1
>>> exp(1e-5) - 1  # gives result accurate to 11 places
1.0000050000069649e-05
>>> expm1(1e-5)    # result accurate to full precision
1.0000050000166668e-05


print(math.exp(1e-5)-1)
print(math.expm1(1e-5))
#1.0000050000069649e-05
#1.0000050000166668e-05

Numeric Functions - math.acos(x)/math.asin(x)/math.atan(x)

• Returns arccosx(x) arcsin(x) acrtan(x), whose values must conform to the values of the defined field of x, otherwise an error is made: math domain error;
• acrsinx domain [-1,1], range [-pi/2,pi/2]
• acrcosx domain [-1,1], range [0,pi]
• actranx domain negative to positive infinity, range [-pi/2,pi/2]
• actcotx domain definition from negative infinity to positive infinity [0,pi]
• All returned are radians

math.acos(x)
Return the arc cosine of x, in radians.

math.asin(x)
Return the arc sine of x, in radians.

math.atan(x)
Return the arc tangent of x, in radians.

Three images: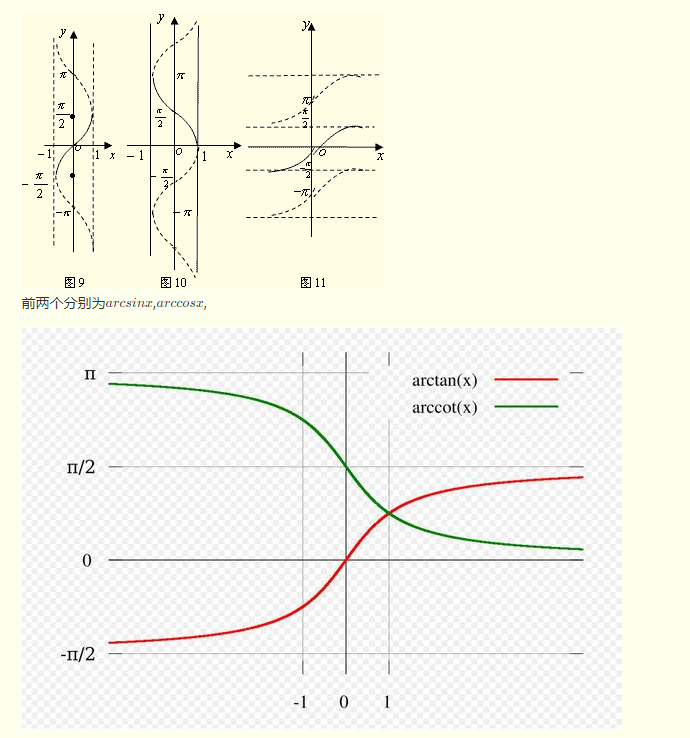

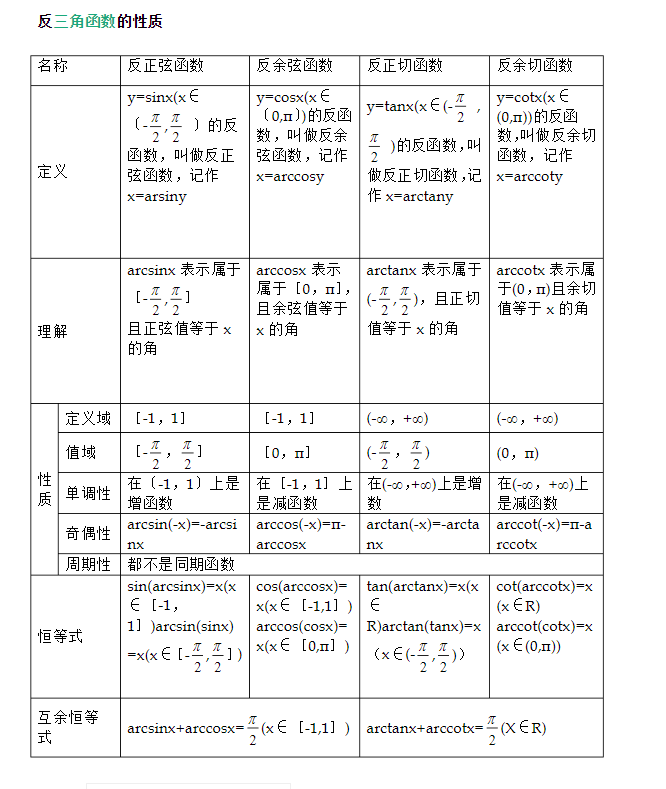
Numeric Function - acrtans2 (y,x)

• Both arctan2 and arctan are used to find the slope.All returned are radian values.However, due to the periodicity of the function, one number corresponds to two radians, etc.For atan (-1), it may be 45 degrees or 225 degrees.[Angles 180 degrees apart have the same tangent and slope]; however, math.atan can only return one value because of "0"; but math.atan2 can calculate two values. Reference file 1Reference File 2

• atan2 = atan2 (y2-y1,x2-x1), so it can generally be used to calculate the slope between two points, math.atan2(y2-y1,x2-x1) is sufficient.

Numeric Functions - math.sin(x)/cos(x)/tanx(x)

• An image, a range defines a domain, and when used, the range of x needs to be satisfied
  
  

Numeric Function - math.hypot(x,y) Distance

• That is, (x x + y y) This is the length of the vector from the origin to the point (x, y)., the distance from the origin to the x,y coordinate point.
• Return floating point number

Return the Euclidean norm, sqrt(x*x + y*y). This is the length of the vector from the origin to point (x, y).

print(math.hypot(3,4)) # 5.0

Numeric Functions - math.degrees(x)/math.radians(x)

• Radian and Angle Conversion

print(math.degrees(math.pi/2))#90.0
print(math.degrees(math.pi/3)) # Question of accuracy 59.999
print(math.radians(90))  # 1.5...

Numeric Function - Hyperbolic Function

• The supplement does not understand its purpose

math.acosh(x)
Return the inverse hyperbolic cosine of x.

math.asinh(x)
Return the inverse hyperbolic sine of x.

math.atanh(x)
Return the inverse hyperbolic tangent of x.

math.cosh(x)
Return the hyperbolic cosine of x.

math.sinh(x)
Return the hyperbolic sine of x.

math.tanh(x)
Return the hyperbolic tangent of x.

Functions that don't know what to do

math.erf(x)
math.erfc(x)
math.gamma(x)
math.lgamma(x)

Numeric Function - Constant

math.pi : π : 3.14...
math.e : e : 2.718...
math.tau:
math.inf: positive infinity
-math.inf: negative infinity
math.nan: Non-numeric

print(math.pi)#3.1415926..
print(math.e)#2.718
print(math.tau)#6.28
print(math.inf)#inf Infinity
print(-math.inf)#-inf
print(math.nan)#nan

Where to add

 |  
 |  Methods defined here:
 |  
 |  __abs__(self, /)
 |      abs(self)
 |  
 |  __add__(self, value, /)
 |      Return self+value.
 |  
 |  __bool__(self, /)
 |      self != 0
 |  
 |  __divmod__(self, value, /)
 |      Return divmod(self, value).
 |  
 |  __eq__(self, value, /)
 |      Return self==value.
 |  
 |  __float__(self, /)
 |      float(self)
 |  
 |  __floordiv__(self, value, /)
 |      Return self//value.
 |  
 |  __format__(...)
 |      float.__format__(format_spec) -> string
 |      
 |      Formats the float according to format_spec.
 |  
 |  __ge__(self, value, /)
 |      Return self>=value.
 |  
 |  __getattribute__(self, name, /)
 |      Return getattr(self, name).
 |  
 |  __getformat__(...) from builtins.type
 |      float.__getformat__(typestr) -> string
 |      
 |      You probably don't want to use this function.  It exists mainly to be
 |      used in Python's test suite.
 |      
 |      typestr must be 'double' or 'float'.  This function returns whichever of
 |      'unknown', 'IEEE, big-endian' or 'IEEE, little-endian' best describes the
 |      format of floating point numbers used by the C type named by typestr.
 |  
 |  __getnewargs__(...)
 |  
 |  __gt__(self, value, /)
 |      Return self>value.
 |  
 |  __hash__(self, /)
 |      Return hash(self).
 |  
 |  __int__(self, /)
 |      int(self)
 |  
 |  __le__(self, value, /)
 |      Return self<=value.
 |  
 |  __lt__(self, value, /)
 |      Return self<value.
 |  
 |  __mod__(self, value, /)
 |      Return self%value.
 |  
 |  __mul__(self, value, /)
 |      Return self*value.
 |  
 |  __ne__(self, value, /)
 |      Return self!=value.
 |  
 |  __neg__(self, /)
 |      -self
 |  
 |  __new__(*args, **kwargs) from builtins.type
 |      Create and return a new object.  See help(type) for accurate signature.
 |  
 |  __pos__(self, /)
 |      +self
 |  
 |  __pow__(self, value, mod=None, /)
 |      Return pow(self, value, mod).
 |  
 |  __radd__(self, value, /)
 |      Return value+self.
 |  
 |  __rdivmod__(self, value, /)
 |      Return divmod(value, self).
 |  
 |  __repr__(self, /)
 |      Return repr(self).
 |  
 |  __rfloordiv__(self, value, /)
 |      Return value//self.
 |  
 |  __rmod__(self, value, /)
 |      Return value%self.
 |  
 |  __rmul__(self, value, /)
 |      Return value*self.
 |  
 |  __round__(...)
 |      Return the Integral closest to x, rounding half toward even.
 |      When an argument is passed, work like built-in round(x, ndigits).
 |  
 |  __rpow__(self, value, mod=None, /)
 |      Return pow(value, self, mod).
 |  
 |  __rsub__(self, value, /)
 |      Return value-self.
 |  
 |  __rtruediv__(self, value, /)
 |      Return value/self.
 |  
 |  __setformat__(...) from builtins.type
 |      float.__setformat__(typestr, fmt) -> None
 |      
 |      You probably don't want to use this function.  It exists mainly to be
 |      used in Python's test suite.
 |      
 |      typestr must be 'double' or 'float'.  fmt must be one of 'unknown',
 |      'IEEE, big-endian' or 'IEEE, little-endian', and in addition can only be
 |      one of the latter two if it appears to match the underlying C reality.
 |      
 |      Override the automatic determination of C-level floating point type.
 |      This affects how floats are converted to and from binary strings.
 |  
 |  __str__(self, /)
 |      Return str(self).
 |  
 |  __sub__(self, value, /)
 |      Return self-value.
 |  
 |  __truediv__(self, value, /)
 |      Return self/value.
 |  
 |  __trunc__(...)
 |      Return the Integral closest to x between 0 and x.
 |  
 |  as_integer_ratio(...)
 |      float.as_integer_ratio() -> (int, int)
 |      
 |      Return a pair of integers, whose ratio is exactly equal to the original
 |      float and with a positive denominator.
 |      Raise OverflowError on infinities and a ValueError on NaNs.
 |      
 |      >>> (10.0).as_integer_ratio()
 |      (10, 1)
 |      >>> (0.0).as_integer_ratio()
 |      (0, 1)
 |      >>> (-.25).as_integer_ratio()
 |      (-1, 4)
 |  
 |  conjugate(...)
 |      Return self, the complex conjugate of any float.
 |  
 |  fromhex(...) from builtins.type
 |      float.fromhex(string) -> float
 |      
 |      Create a floating-point number from a hexadecimal string.
 |      >>> float.fromhex('0x1.ffffp10')
 |      2047.984375
 |      >>> float.fromhex('-0x1p-1074')
 |      -5e-324
 |  
 |  hex(...)
 |      float.hex() -> string
 |      
 |      Return a hexadecimal representation of a floating-point number.
 |      >>> (-0.1).hex()
 |      '-0x1.999999999999ap-4'
 |      >>> 3.14159.hex()
 |      '0x1.921f9f01b866ep+1'
 |  
 |  is_integer(...)
 |      Return True if the float is an integer.
 |  
 |  ----------------------------------------------------------------------
 |  Data descriptors defined here:
 |  
 |  imag
 |      the imaginary part of a complex number
 |  
 |  real
 |      the real part of a complex number

None

Process finished with exit code 0