1, Purpose and requirements:
1. Familiar with the theory and method of solving linear equations;
2. Be able to prepare column principal component elimination method, LU decomposition method, Jacobian and Gauss Seidel iterative Fard procedures;
3. Through practical calculation, we can further understand the advantages and disadvantages of various methods and select the appropriate numerical method.
2, Experimental content
1. Column principal component Gaussian elimination method
- algorithm
The equation is used as an augmented matrix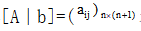
express
1. Elimination process
For k=1,2,..., n-1
① Select the primary element and find the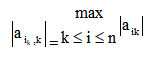
② If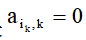
, then matrix A is singular and the program ends; Otherwise, execute ③.
③ If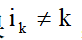
, then swap lines k and
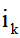Row corresponding element position
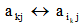j=k,┅,n+1
④ Elimination, calculation for i=k+1,?, n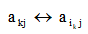
Calculate for j=l+1,?, n+1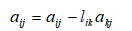
2. Back substitution process
- Programs and examples
- Program code
#include<stdio.h>
double A[10][10];
double B[10];
double X[10];
int n;
void swap_row(int a, int b)
{
double t;
int i;
for (i = 1; i <= n; i++)
{
t = A[a][i];
A[a][i] = A[b][i];
A[b][i] = t;
}
t = B[a];
B[a] = B[b];
B[b] = t;
}
int find_rowmax(int k, int n){
int rowmax = k;
double max = 0;
int i;
for (i = k; i <= n; i++)
{
if (max < fabs(A[i][k]))
{
max = fabs(A[i][k]);
rowmax = i;
}
}
if (rowmax != k)
swap_row(rowmax, k);
if (max == 0)
{
return 1;
}
else return 0;
}
void print_matrix(int k)
{
int i;
int j;
printf("\n step %d\n",k);
printf("Augmented matrix: \n");
for (i = 1; i <= n; i++)
{
for (j = 1; j <= n; j++)
{
printf("%f", A[i][j]);
printf(" ");
}
printf("%lf", B[i]);
printf("\n");
}
}
int main()
{
int i,j,k,l,m;
double t;
clrscr();
printf("Please enter the order of the coefficient matrix:");
scanf("%d", &n);
printf("Please enter augmented matrix: \n");
for (i = 1; i <= n; i++)
{
for (j = 1; j <= n; j++)
{
scanf("%lf", &t);
A[i][j] = t;
}
scanf("%lf", &t);
B[i] = t;
}
for (k = 1; k < n; k++)
{
int flag = find_rowmax(k, n);
if (flag == 1)
{
return 0;
};
for (l = k + 1; l <= n; l++)
{
double q = A[l][k] / A[k][k];
for (m = k; m <= n; m++)
{
A[l][m] -= q * A[k][m];
}
B[l] -= q * B[k];
}
print_matrix(k);
}
for (i = n; i >= 1; i--)
{
for (j = n; j > i; j--)
{
B[i] -= A[i][j] * X[j];
}
X[i] = B[i] / A[i][i];
}
printf("result:");
for (i = 1; i <= n; i++)
{
printf("\nx[%d] = %lf", i,X[i]);
printf(" ");
}
getch();
}- experimental result
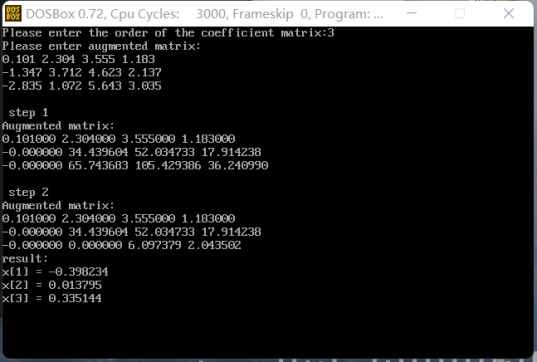
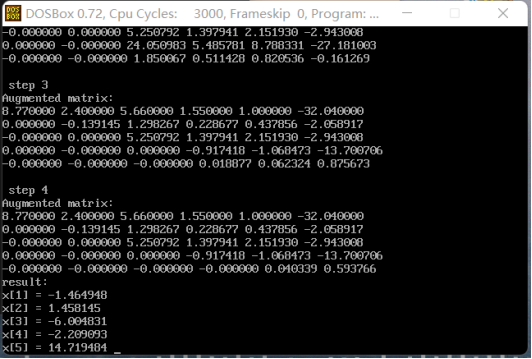
2. Matrix direct triangular decomposition method
- algorithm
Decompose A in the equation set Ax=b into A=LU, where L is the unit lower triangular matrix and U is the upper triangular matrix, then the equation set Ax=b is transformed into solving two equation sets Ly=b and Ux=y. The specific algorithm is as follows:
① Calculate for j=1,2,3,..., n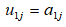
Calculate for i=2,3,..., n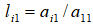
② For k=1,2,3,..., n:
a. Calculate for j=k,k+1,..., n
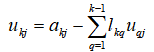
b. Calculate for i=k+1,k+2,..., n
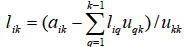
③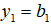
, calculate for k=2,3,..., n
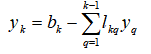
④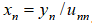
, for k=n-1,n-2,..., 2,1
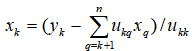
Note: since the formula for calculating u is the same as that for calculating y, the augmented matrix can be calculated directly
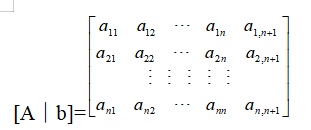
Implement algorithms ② and ③. At this time, the n+1 column element of U is y.
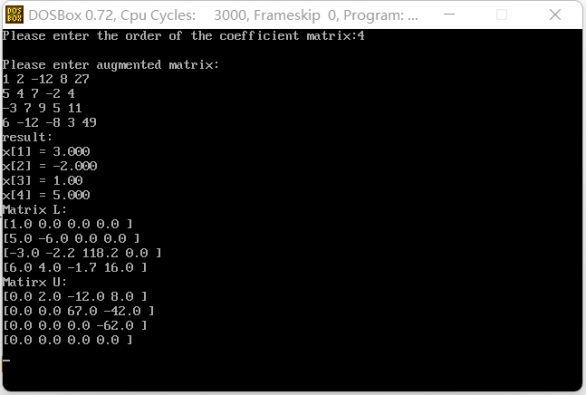
- Programs and examples
- Program code
#include <stdio.h>
#include <stdlib.h>
double a[20][20],x[20];
int main()
{
float aaa,*bbb=&aaa;
int n;
int i, j, k,r;
double* x;
clrscr();
printf("Please enter the order of the coefficient matrix:");
scanf("%d", &n);
if (n > 20)
{
return 1;
}
if (n <= 0)
{
return 1;
}
printf("\nPlease enter augmented matrix: \n");
for (i = 0; i < n; i++) {
for (j = 0; j < n+1; j++)
{
scanf("%lf", &a[i][j]);
}
}
x = (float*)malloc(n * sizeof(float));
for (r = 0; r <= n - 1; r++)
{
for (i = r; i <= n; i++)
for (k = 0; k <= r - 1; k++)
a[r][i] -= a[r][k] * a[k][i];
for (i = r + 1; i <= n - 1; i++)
{
for (k = 0; k <= r - 1; k++)
a[i][r] -= a[i][k] * a[k][r];
a[i][r] /= a[r][r];
}
}
for (i = n - 1; i >= 0; i--)
{
for (r = n - 1; r >= i + 1; r--)
a[i][n] -= a[i][r] * x[r];
x[i] = a[i][n] / a[i][i];
}
printf("result:\n");
for (i = 0; i < n; i++) {
printf("x[%d] = %.3f\n", i+1, x[i]);
}
printf("Matrix L:\n");
for (i = 0; i < n; i++)
{
printf("[");
for (j = 0; j <=i ; j++)
{
printf("%.1f ",a[i][j]);
}
for (j = i+1; j < n; j++)
{
printf("0.0 ");
}
printf("]\n");
}
printf("Matirx U:\n");
for (i = 0; i < n; i++)
{
printf("[");
for (j = 0; j <= i; j++)
{
printf("0.0 ");
}
for (j = i+1; j < n; j++)
{
printf("%.1f ", a[i][j]);
}
printf("]\n");
}
getch();
return 0;
} 
3. Iterative method
3.1} Jacobian iterative method
- algorithm
Let the equation set Ax=b be the diagonal element of the coefficient matrix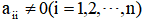
, M is the maximum allowable number of iterations, ε Is the allowable error.
① Take initial vector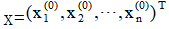
, let k=0.
② Calculate for i=1,2,..., n
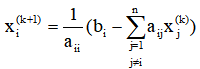
③ If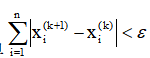
, then output
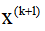, end; Otherwise, execute ④.
④ If k ≥ M, it does not converge and the program is terminated; otherwise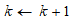
, turn ②.
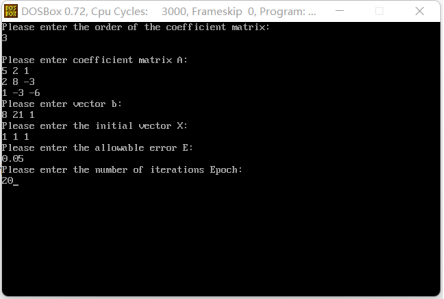
- Programs and examples
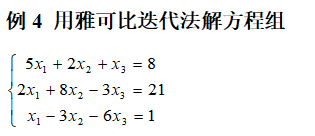
- Program code
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define MaxSize 20
double A[MaxSize][MaxSize];
double B[MaxSize];
double D[MaxSize][MaxSize];
double E[MaxSize][MaxSize];
double F[MaxSize];
double X[MaxSize];
double X1[MaxSize];
float e;
int n;
int epoch;
void InitMatrix()
{
int i, j;
for (i = 0; i < n; i++)
for (j = 0; j < n; j++)
{
if (i == j)
{
D[i][j] = 1 / A[i][i];
E[i][j] = 0;
}
if (i < j)
E[i][j] = A[i][j];
if (i > j)
E[i][j] = A[i][j];
}
}
void Jacobi()
{
int i, j, k, r;
double sum1, sum2 = 0;
for (i = 0; i < n; i++)
for (j = 0; j < n; j++)
{
sum1 = 0;
for (k = 0; k < n; k++)
{
sum1 = sum1 + D[i][k] * E[k][j];
}
E[i][j] = -sum1;
}
for (i = 0; i < n; i++)
{
sum2 = 0;
for (k = 0; k < n; k++)
{
sum2 = sum2 + D[i][k] * B[k];
}
F[i] = sum2;
}
for (r = 1; r < epoch; r++)
{
int flag = 0;
double sum3;
for (i = 0; i < n; i++)
X1[i] = X[i];
for (i = 0; i < n; i++)
{
sum3 = 0;
for (k = 0; k < n; k++)
{
sum3 = sum3 + E[i][k] * X1[k];
}
X[i] = F[i] + sum3;
}
for (j = 0; j < n; j++)
if (fabs(X[j] - X1[j]) < e)
flag++;
if (flag == n)
{
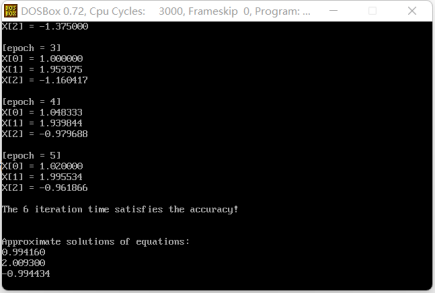
printf("\nThe %d iteration time satisfies the accuracy!\n", r);
break;
}
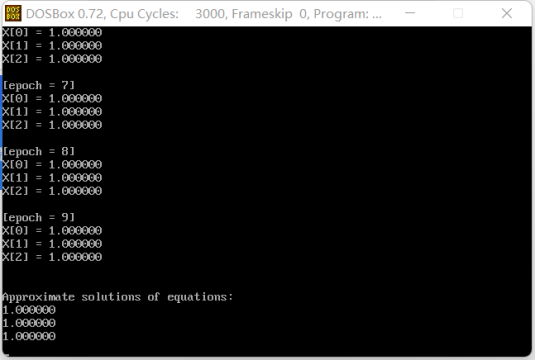
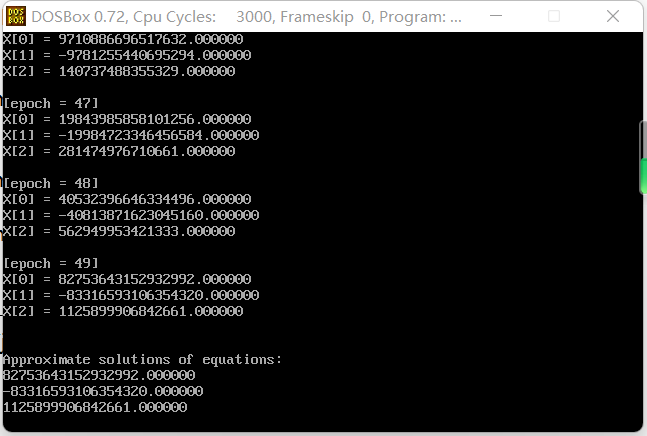
printf("\n[epoch = %d] \n", r);
for (i = 0; i < n; i++)
printf("X[%d] = %lf\n", i, X[i]);
}
}
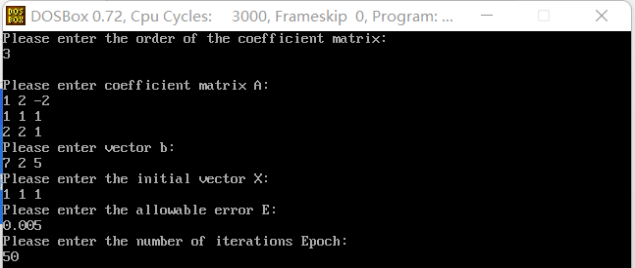
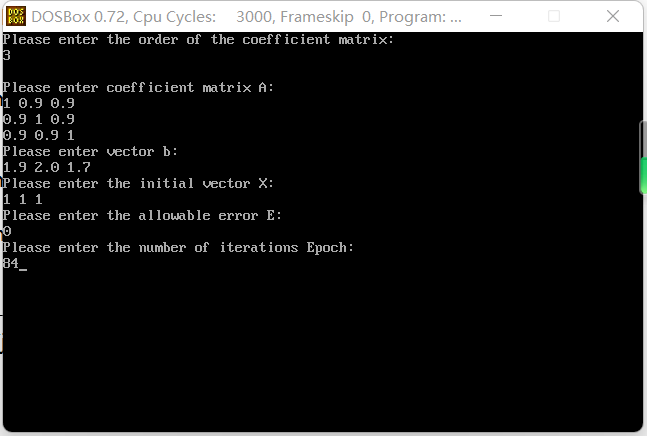
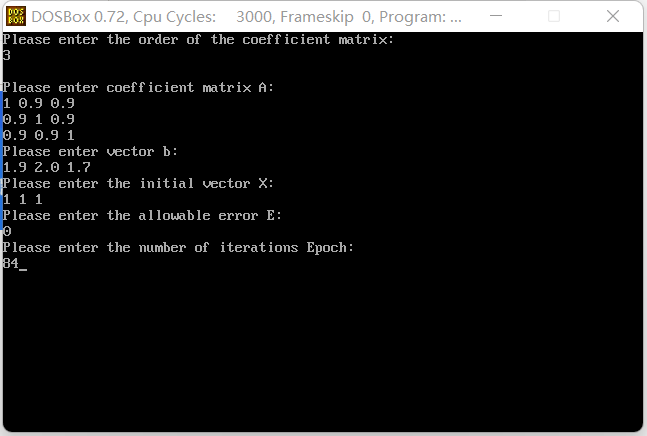
void input()
{
int i, j;
printf("Please enter coefficient matrix A:\n");
for (i = 0; i < n; i++)
for (j = 0; j < n; j++)
scanf("%lf", &A[i][j]);
printf("Please enter vector b:\n");
for (i = 0; i < n; i++)
scanf("%lf", &B[i]);
printf("Please enter the initial vector X:\n");
for (i = 0; i < n; i++)
scanf("%lf", &X[i]);
printf("Please enter the allowable error E:\n");
scanf("%f", &e);
printf("Please enter the number of iterations Epoch:\n");
scanf("%d", &epoch);
}
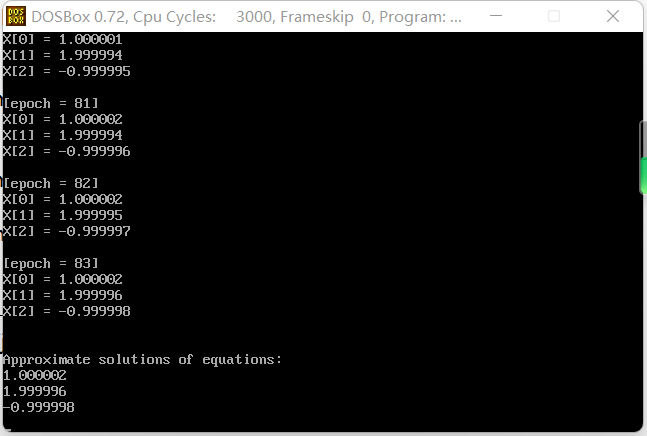
void print()
{
int i;
printf("\n\nApproximate solutions of equations:\n");
for (i = 0; i < n; i++)
printf("%lf\n", X[i]);
}
int main()
{
clrscr();
printf("Please enter the order of the coefficient matrix: \n");
scanf("%d", &n);
printf("\n");
input();
InitMatrix();
Jacobi();
print();
getch();
return 0;
} 
3.2 Gauss zelder iterative method
- algorithm
Let the diagonal elements of the coefficient matrix of the equation system Ax=b,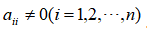
, M is the maximum allowable number of iterations, ε Is the allowable error
① Take initial vector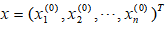
, let k=0.
② Calculate for i=1,2,..., n
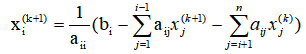
③ If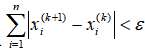
, then output
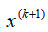, end; Otherwise, execute ④.
④ If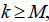
Then it does not converge and the program is terminated; otherwise
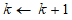, turn ②.
- Programs and examples
- Program code
#include <stdio.h> #include <stdlib.h> #include <math.h> #define MaxSize 20 double A[MaxSize][MaxSize]; double B[MaxSize]; double D[MaxSize][MaxSize]; double E[MaxSize][MaxSize]; double F[MaxSize]; double X[MaxSize]; double X1[MaxSize]; float e; int n; int epoch; void InitMatrix() { int i, j; for (i = 0; i < n; i++) for (j = 0; j < n; j++) { if (i == j) { D[i][j] = 1 / A[i][i]; E[i][j] = 0; } if (i < j) E[i][j] = A[i][j]; if (i > j) E[i][j] = A[i][j]; } } void GauseSeidel() { int i, j, k, r; double sum1, sum2 = 0; for (i = 0; i < n; i++) for (j = 0; j < n; j++) { sum1 = 0; for (k = 0; k < n; k++) { sum1 = sum1 + D[i][k] * E[k][j]; } E[i][j] = -sum1; } for (i = 0; i < n; i++) { sum2 = 0; for (k = 0; k < n; k++) { sum2 = sum2 + D[i][k] * B[k]; } F[i] = sum2; } for (r = 1; r < epoch; r++) { int flag = 0; double sum3; for (i = 0; i < n; i++) X1[i] = X[i]; for (i = 0; i < n; i++) { sum3 = 0; for (k = 0; k < n; k++) { if (k < i) { sum3 = sum3 + E[i][k] * X[k]; } else{ sum3 = sum3 + E[i][k] * X1[k]; } X[i] = F[i]+sum3; } } for (j = 0; j < n; j++) if (fabs(X[j] - X1[j]) < e) flag++; if (flag == n) { printf("\nThe %d iteration time satisfies the accuracy!\n", r); break; } printf("\n[epoch = %d] \n", r); for (i = 0; i < n; i++) printf("X[%d] = %lf\n", i, X[i]); } } void input() { int i, j; printf("Please enter coefficient matrix A:\n"); for (i = 0; i < n; i++) for (j = 0; j < n; j++) scanf("%lf", &A[i][j]); printf("Please enter vector b:\n"); for (i = 0; i < n; i++) scanf("%lf", &B[i]); printf("Please enter the initial vector X:\n"); for (i = 0; i < n; i++) scanf("%lf", &X[i]); printf("Please enter the allowable error E:\n"); scanf("%f", &e); printf("Please enter the number of iterations Epoch:\n"); scanf("%d", &epoch); } void print() { int i; printf("\n\nApproximate solutions of equations:\n"); for (i = 0; i < n; i++) printf("%lf\n", X[i]); } int main() { clrscr(); printf("Please enter the order of the coefficient matrix: \n"); scanf("%d", &n); printf("\n"); input(); InitMatrix(); GauseSeidel(); print(); getch(); return 0; }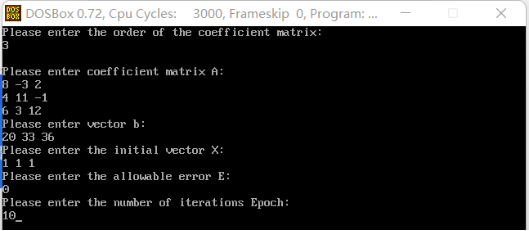
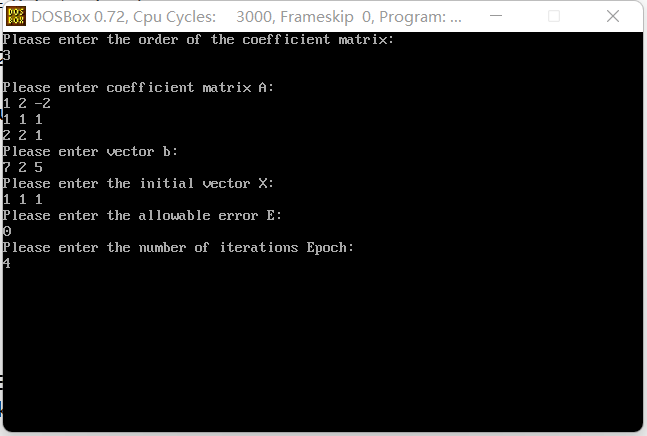
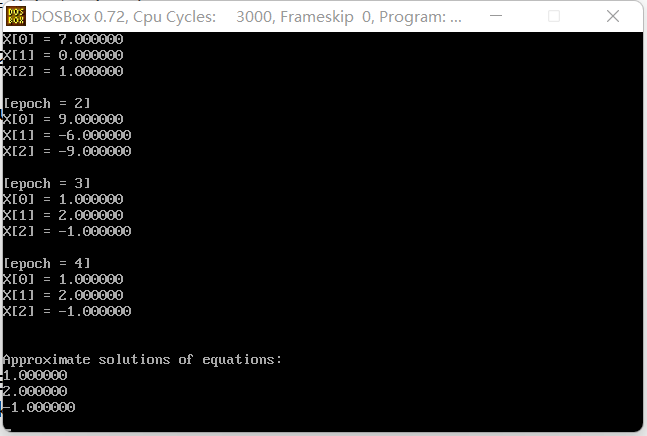
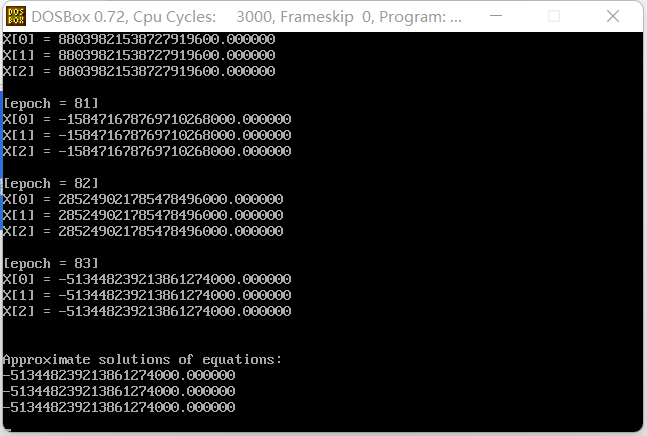
3, Analysis and thinking
In this experiment, the linear equations are solved by column principal element elimination method, direct triangular decomposition method and iterative method in C language. Regardless of the rounding error caused by the number of floating-point numbers, both the column principal component elimination method and the direct triangular decomposition method can obtain the exact solution, but the iterative method needs to give an error limit to determine the end of the iteration.