Introduction to Numpy array

All functions in Numpy are based on the N-dimensional array data structure ndarray.

ndarray is a collection of data of the same type. The index of elements starts with the subscript 0.
Unlike python's List, each element in ndarray has an area of the same storage size in memory.

Numpy supports different data types from python native types. The storage space length of each data type is fixed.
Common data types are as follows (numpy is usually referenced by import numpy as np):

• np.void

• np.bool_ : Boolean type

• np.object_ : Any object

• np.bytes_ : Byte sequence

• np.str_ : character

• np.unicode_ : character string

• np.int_ : Shaping, automatically converted to int32, int64 and other types according to the system platform

• np.float_ : Floating point type, which is automatically converted to float32, float64 and other types according to the system platform

• np.complex_ : The complex number is automatically converted to complex64, complex128 and other types according to the system platform

• Integers type

  • np.byte: byte
  • np.int8: 8-bit integer
  • np.int16: 16 bit integer
  • np.int32: 32-bit integer
  • np.int64: 64 bit integer

• Unsigned integers type

  • np.ubyte: bytes
  • np.uint8: 8-bit uint
  • np.uint16: 16 bit uint
  • np.uint32: 32-bit uint
  • np.uint64: 64 bit uint

• Floating point numbers type

  • np.float16: 16 bit float
  • np.float32: 32-bit float
  • np.float64: 64 bit float
  • np.float96: 96 bit float
  • np.float128: 128 bit float

• Complex floating point numbers type

  • np.complex64: two 32-bit floating-point numbers
  • np.complex128: two 64 bit floating point numbers
  • np.complex192: two 96 bit floating point numbers
  • np.complex256: two 128 bit floating point numbers

numpy also has some NP short，np.half，np.longlong and other aliases. Not recommended

When creating a Numpy array, you can specify the python native type, but it will be automatically converted to the corresponding Numpy data type.

Numpy is actually written in C language, and its data type basically corresponds to the data type of C language.

Mind map

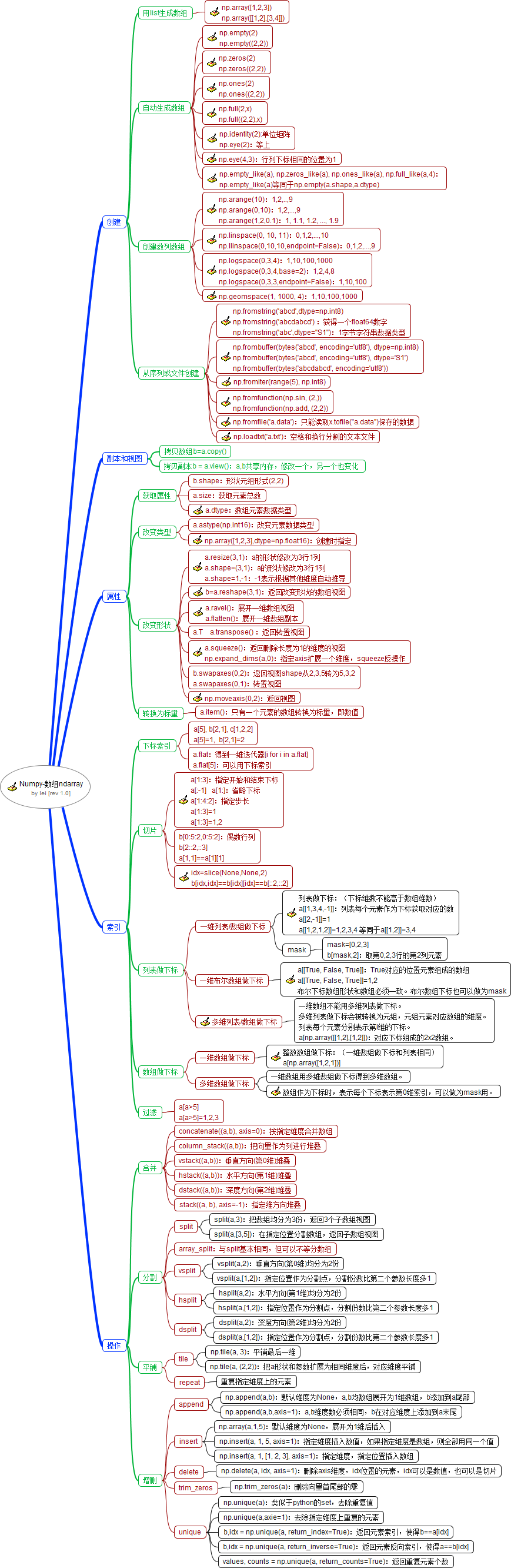
Create Numpy array

Creating arrays with python sequences

arr1 = np.array([1,2,3])              #List, set and tuple can be used as parameters
arr2 = np.array([[1,2],[3,4]])       #Create multidimensional array

The innovative array does not share memory with the list in the parameter.

arr1 = np.array([1,2,3], np.int8)                       #Specify data type
arr2 = np.array([1,2,3], dtype=np.float16)       #Specify data type

Auto generate array

Common array generation

Create special arrays such as all 0, all 1 and identity matrix

np.empty(2)                 #Element only allocates memory and does not initialize 
np.empty((2, 2))           #Multidimensional array, parameter must be tuple. Lists and other sequences are automatically converted to tuples.

np.zeros(2)                  #All elements are zero 
np.zeros((2, 2))            #Multidimensional all zero array

np.ones(2)                  #All elements are 1
np.ones((2, 2))            #Multidimensional all 1 array

np.full(2, x)                 #All element values are x
np.full((2,2), x)            #All multidimensional elements are the same array

np.identity(2)             #two × 2 identity matrix, diagonal is 1, and other values are 0 

np.eye(2)                  #two × 2 identity matrix
np.eye(2, 2)              #two × 2 identity matrix. Note that the eye method is special, and the parameter is not a tuple
np.eye(4, 3)              #Similar to identity matrix. The same position of the matrix subscript is 1, and the other values are zero

All creation methods can use the dtype parameter to specify the data type. If not specified, the default is float type:

np.empty((2, 2), dtype=np.float_)
np.zeros((2, 2), dtype=np.float16)
np.ones((2, 2), dtype=np.float32)
np.full((2,2), 3, dtype=np.int8)
np.identity(2, dtype=np.int16)
np.eye(3, 2, dtype=np.complex_)

Create an array based on the shape and data type of an existing array

np.empty_like(a)    #Equivalent to NP Empty (shape of a, data type of dtype=a) 
np.zeros_like(a)
np.ones_like(a)
np.full_like(a, 4) 

No identity_like and eye_like

Array generation

Range range array

np. Range (start = 0, end, step = 1): generate a sequence of [start, end) intervals with step.

np.arange(10)    #[0, 10) array with step size of 1. Note that it is an array, not a range. It should mean array range. 
np.arange(1, 5)    #[1, 2, 3, 4]
np.arange(0.1, 0.5, 0.1)    #[0.1, 0.2, 0.3, 0.4]

np.arange(1, 5, dtype=np.float16)    #Specify data type

Arithmetic array

np.linsapce(start,end,count=50,endpoint=True): create an arithmetic sequence with [start, end] elements count.
You can specify whether to include the final value through the endpoint parameter. The final value is included by default.

np.linspace(0, 10, 11)     # [0, 1, 2, ..., 10]
np.llinspace(0, 10 , 10, endpoint=False)    #[0, 1, 2, ..., 9] 

np.linspace(1, 50)    #[1, 2, 3,..., 50] the default number of elements is 50.

Note that linspace is not linespace.

Proportional sequence

logspace(start, stop, num=50, endpoint=True, base=10.0):
An equal ratio sequence with base as base and linspace(sart, stop, num) as power.
That is, an equal ratio sequence is created by specifying the start index, end index, number of elements, and cardinality.

np.logspace(0, 3, 4)    #[1,101001000] i.e. [10 * * 0, 10 * * 1, 10 * * 2, 10 * * 3] 
np.logspace(0, 3, 4, base=2)    #[1,2,4,8] i.e. [2 * * 0, 2 * * 1, 2 * * 2, 2 * * 3]
np.logspace(0, 3, 3, endpoint=False)    #[1,10100] i.e. [10 * * 0, 10 * * 1, 10 * * 2]

Geospace (start, stop, Num = 50, endpoint = true) the start element is start,
The end element is end and the number of elements is num.

np.geomspace(1, 1000, 4)    #[1,10,100,1000]
np.geomspace(2, 16, 3, endpoint=False)    #[2,4,8]

Create an equal ratio sequence according to the beginning and end and the number. The first number cannot be 0.

np. linspace, np. logspace, np. Geospace can also specify the data type with the dtype parameter.

Create from memory sequence or file

Create from string

np.fromstring('abc', dtype=np.int8)    #The number of string bytes must be an integer multiple of the length of the data type. dtype is specified as NP Int16 will make an error.
np.fromstring('abcdabcd')    #Get a float64 number (result on a 64 bit computer). The number of string bytes must be a multiple of 64.

#Character arrays cannot directly use NP str_, np.bytes_, Or NP unicode_， The number of bytes of STR must be specified.
np.fromstring('abc',dtype="S1")    # 1-byte string data type. The actual type is NP bytes_
np.fromstring('abcd',dtype="S2")    #2-byte string data type.
np.fromstring('abcdabcd',dtype="U2")    #2-byte Unicode string data type. The actual type is NP str_
#For Chinese, the coding of characters is usually segmented, so it is not suitable for processing Chinese. 

It is recommended that both fromstring explicitly specify dtype because the default data type is float. The number of string bytes must be a multiple of float.

Data types S1,S2,S3,S4... Sn represent strings of n bytes in length.

Create from cache

np. From buffer is similar to NP Fromstring, but its first parameter is byte sequence.

np.frombuffer(b'abcdabcd')    #Same as NP fromstring('abcdabcd')
np.frombuffer(bytes('abcd', encoding='utf8'), dtype=np.int8)
np.frombuffer(bytes('abcd', encoding='utf8'), dtype='S1')
 
np.frombuffer(buff, dtype='S1', count=5, offset=6)    #Read 5 S1 type data from the 6th byte. 

Create from iterator

np.fromiter(range(5), np.int8)    #dtype must be specified. 

Create from function

np. From function (f, t): f is a function and t is a tuple. Generate an array with shape T,
The element of the array is the value calculated by the function f, and the parameters of the function are:

• One dimensional array: function parameters are element subscripts.
• Multidimensional array: the function parameter is the subscript of dimension 0.
• n parameter function: the dimension should be the same as the function dimension.

The second parameter is the shape of the array, which must be a tuple.

np.fromfunction(np.abs, (2,))    #[0, 1, 2]
np.fromfunction(np.abs, (2,2))    #[[0,1], [1,1]]

np.fromfunction(np.add, (2,2))   #[[0,1], [1,2]]

create from file

np.loadtxt('a.txt')    #Space and newline split text files. The number of data in each row must be the same 

arr1.tofile('a.data')    #Save array to file
np.fromfile('a.data')    #Only data saved by x.tofile("a.data") can be read.
#np. The data read by fromfile is a one-dimensional array. No matter how many dimensions are saved, they are one-dimensional after reading. 

Array copies and views

arr2 = arr1.copy()    #Get a copy of the arr1 array. arr2 and arr1 do not share memory.
arr3 = arr1.view()    #Get a view of the arr1 array. arr3 and arr1 share memory. If you modify one, the other will change.

Array properties

get attribute

arr1.shape    #Get the array shape and output it as tuple in the form of (2,2)
arr1.size       #Gets the total number of elements
arr1.dtype    #Gets the array element data type

Change array data type

arr2 = arr1.astype(np.int16)    #Change the element data type. arr2 and arr1 do not share memory

arr1.dtype = np.float16    #Directly change the data type of the array, and the data memory remains unchanged.

It is not recommended to directly assign a value to dtype. For an array of int8 data types, when dtype is modified to int16, two data will be merged into one.
The shape of the array will also change automatically.

Change array shape

a.resize(3,1)    #Modify the shape of array a to 3 rows and 1 column
a.resize(3,-1)   #-1 indicates automatic derivation based on other data. For example, if there are 9 elements, the shape is (3,3), and if there are 6 elements, the shape of the array is (3,2)

a.shape=(3,1)    #The shape of a is changed to 3 rows and 1 column
a.shape=(1,-1)   #-1 indicates automatic derivation according to other dimensions 

b=a.reshape(3,1)    #Returns an array view that changes shape. a. B different shapes, but shared memory. Modifying one will change the other 

Array transpose

a.T                   #Returns the transposed view of array a
a.transpose()    #Returns the transposed view of array a

Flatten arrays

b = a.ravel()    #Returns the view that expands the array into a one-dimensional array. A and B share memory

b = a.flatten()    #Returns a copy of an array expanded into a one-dimensional array. A and B do not share memory

Dimension operation with length 1

b = a.squeeze()    #Delete the dimension with length 1 and return to the view.
#If a = NP Array ([[[1,2,3]]]), the returned b value is [1,2,3]

b = np.expand_dims(a,0)    #Specifying axis=0 extends the view of a dimension, which is equivalent to the reverse operation of squeeze 

Row vector a = NP Array ([1,2,3]) is converted to column vector, B = NP expand_ dims(a,0).
Note that only NP expand_ It is called in dims mode, and it is called directly with different arrays.

b.swapaxes(0,2)    #Return to view shape from 2,3,5 to 5,3,2
a.swapaxes(0,1)    #Transpose view 
 
np.moveaxis(a,0,2)    #Return to the view. The shape changes from 2,3,5 to 3,5,2. Different from swaaxes. 

Note that the array has no moveaxis method.

Convert to scalar

b = a.item()    #Convert an array with only one element to scalar, that is, an array in the form of [1] or [[[1]]] can be converted to scalar 1

Indexing and slicing

Subscript index

b = a[5]    #Same as python list. Gets the element with subscript 5
b = a[-1]    #Same as python list. Gets the last to last element

#Multidimensional array
b = a[2][1]    #Same as Python list. First get the 2-row array, and then get the first column element, that is, the element with subscript (2,1).

b = a[2,1]    #Same as b=a[2][1] 

b = a.flat[2]    #The flat attribute of the array can get a special one-dimensional iterator (which can be indexed by subscript), equivalent to a. travel() [2]

It can be assigned directly, such as a[5]=1,a[2][-1]=2

section

b = a[1:3]    #The same as python list, get the data view with 1 to 3 subscripts, excluding a[3]
b = a[:-1]    #Same as python list, omitting the starting subscript
b =  a[:]      #Like python list, omit the subscript to obtain the view of the entire array
b = a[1:4:2]    #Specify the step size, that is, get the array view with subscripts 1 and 3

b = a[::2, ::2]    #Get even rows and columns

a[1:3]=1    #Assignment, all elements are assigned 1
a[1:3]=1,2    #The number of assignments is the same as the number of elements.

Slice type

idx = slice(None,None,2)    #Create a slice index. None means to omit the value, which is equivalent to:: 2
#a[idx,idx], a[idx][idx], a[::2,::2] same

python list as subscript

Subscript one-dimensional numeric list

b = a[[1,2,1,2]]    #A new array composed of a[1],a[2],a[1],a[2] is not a view, but a copy of the elements

#However, a[[1,2]]=3,4 can change the value of elements in a.

You can repeatedly take multiple values for the same element

One dimensional Boolean list as subscript (the shape of the subscript must be the same as that of the array)

a[[True, False, True]]    #An array of position elements corresponding to True, that is, a view composed of a [0] and a [2] elements
a[[True, False, True]]=1,2

In the old version of Boolean array, true and false are regarded as 1 and 0 respectively

Multidimensional list as subscript

The subscript of multidimensional list will be automatically converted to tuple, and the tuple element corresponds to the dimension of the array.
The number of elements in the list cannot be greater than the dimension of the array

a[[i,j,k]]   #i. Both J and K can be arrays, and both can be multidimensional arrays

numpy array as subscript

Subscript one-dimensional array (the same as one-dimensional list)

a[ np.array([1,2]) ]    #Same as a[[1,2]]. 

Subscript multidimensional array

• A one-dimensional array uses a multi-dimensional array as a subscript to obtain a multi-dimensional array. The array elements are the data corresponding to the position of the subscript elements.
• When a multidimensional array is used as a subscript, each subscript represents the index of the 0th dimension of the array.

A multi-dimensional array (np.array) as a subscript is equivalent to the first element of a tuple when a list is used as a subscript.

filter

Boolean transport is used as the subscript.

a[a>5]    #Gets the view of an element with a value greater than 5
a[a>5]=1,2,3 

Array operation

Array merge

Merge by specified dimension (np.concatenate)

>>> a = np.array([[1, 2], [3, 4]])
>>> b = np.array([[5, 6]])
>>> np.concatenate((a, b), axis=0)
array([[1, 2],
       [3, 4],
       [5, 6]])
>>> np.concatenate((a, b.T), axis=1)
array([[1, 2, 5],
       [3, 4, 6]])
>>> np.concatenate((a, b), axis=None)
array([1, 2, 3, 4, 5, 6])

Stack vertically (rows) (np.vstack)

>>> a = np.array([1, 2, 3])
>>> b = np.array([4, 5, 6])
>>> np.vstack((a,b))
array([[1, 2, 3],
          [4, 5, 6]])

Note that a one-dimensional array becomes a two-dimensional array after merging. When concatenate is used for merging, it will still be a one-dimensional array after merging.

Stack horizontally (columns) (np.hstack)

a = np.array([1,2,3])
b = np.array([4,5,6])
np.hstack((a,b))
array([1, 2, 3, 4, 5, 6])

a = np.array([[1],[2],[3]])
b = np.array([[4],[5],[6]])
np.hstack((a,b))
array([[1, 4],
       [2, 5],
       [3, 6]])

Stack one-dimensional arrays as columns (np.column_stack)

>>> a = np.array((1,2,3))
>>> b = np.array((2,3,4))
>>> np.column_stack((a,b))
array([[1, 2],
       [2, 3],
       [3, 4]])

Stack by depth (3rd axis) (np.dstack)

>>> a = np.array([1,2,3))
>>> b = np.array([2,3,4])
>>> np.dstack((a,b))
array([[[1, 2],
        [2, 3],
        [3, 4]]])
        
        
>>> a = np.array([[1],[2],[3]])
>>> b = np.array([[2],[3],[4]])
>>> np.dstack((a,b))
array([[[1, 2]],
       [[2, 3]],
       [[3, 4]]])

For arrays with less than 3 dimensions, add a dimension with length of 1 at the tail. That is, the array shape is automatically converted from (M,N) to (M,N,1)

Stack along the specified axis (np.stack)

>>> np.stack((a, b), axis=-1)
array([[1, 4],
       [2, 5],
       [3, 6]])

The axis value cannot be greater than the number of dimensions, so you cannot stack vectors like hstack

Array partition

Separate the array along the specified axis to get the view (np.split)

Specify the split size (must be able to divide equally)

>>> x = np.arange(9)
>>> np.split(x, 3)
[array([0,  1,  2]), array([3,  4,  5]), array([6,  7,  8])]

Specify split location

>>> x = np.arange(8)
>>> np.split(x, [3, 5, 6, 10])
[array([0,  1,  2]),
 array([3,  4]),
 array([5]),
 array([6,  7]),
 array([], dtype=float64)]

You can specify the axis of the split with the axis parameter

Split the array along the specified axis to get the view (np.array_split)

And NP The only difference of split is that it can be divided unequally

>>> x = np.arange(8.0)
>>> np.array_split(x, 3)
[array([0.,  1.,  2.]), array([3.,  4.,  5.]), array([6.,  7.])]

vsplit， hsplit， dsplit

It indicates that the array is divided in the vertical (0th dimension), horizontal (1st dimension) and depth (2nd dimension) directions respectively.
Similar usage

>>> x = np.arange(8).reshape(4, 2)
array([[0, 1],
       [2, 3],
       [4, 5],
       [6, 7]])
>>> np.vsplit(x,2) #Only equal
[array([[0, 1],
       [2, 3]]), 
 array([[4, 5],
       [6, 7]])]
>>> np.vsplit(x, [1,2])
[array([[0, 1]]),
 array([[2, 3]]),
 array([[4, 5],
       [6, 7]])]

Array tiling

Tile (np.tile)

Simple tiling

>>> a=np.array([1,2,3])
>>> np.tile(a,2)
array([1, 2, 3, 1, 2, 3])

>>> a=np.array([[1,2],[3,4]])
array([[1, 2],
       [3, 4]])
>>> np.tile(a,2)   #Tile in - 1 dimension direction
array([[1, 2, 1, 2],
       [3, 4, 3, 4]])

Multidimensional tiling (parameter is tuple)

Principle:

• First, the shape of the array and the shape of the parameter are extended to the same dimension
  • Extension method, (M,N) is extended to the form of (1,M,N), (1,1,M,N)
• Then tile the corresponding dimension

>>> a = np.array([0, 1, 2])
>>> np.tile(a, (2, 2))
array([[0, 1, 2, 0, 1, 2],
       [0, 1, 2, 0, 1, 2]])

>>> a = np.array([[1,2],[3,4]])
>>> np.tile(a, (2,1,2))
array([[[1, 2, 1, 2],
        [3, 4, 3, 4]],
       [[1, 2, 1, 2],
        [3, 4, 3, 4]]])

Repeat (np.repeat)

Repeats the element on the specified dimension.

>>> np.repeat(3, 4)
array([3, 3, 3, 3])

>>> x = np.array([[1,2],[3,4]])
>>> np.repeat(x, 2)  #axis=None
array([1, 1, 2, 2, 3, 3, 4, 4])

>>> np.repeat(x, 3, axis=1)
array([[1, 1, 1, 2, 2, 2],
       [3, 3, 3, 4, 4, 4]])

Array addition and deletion

Tail append

No dimension is specified, that is, the default value is axis=None. Both the meta array and the append array are expanded into a one-dimensional array and appended.

>>> np.append([1, 2, 3], [[4, 5, 6], [7, 8, 9]])
array([1, 2, 3, ..., 7, 8, 9])

Specify the dimension. The number of dimensions of the original array and the appended array must be the same.

>>> np.append([[1, 2, 3], [4, 5, 6]], [[7, 8, 9]], axis=0)
array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

>>> np.append([[1, 2, 3], [4, 5, 6]], [7, 8, 9], axis=0)
Traceback (most recent call last):
    ...
ValueError

Insert element

No dimension is specified. The default is axis=None

>>> a = np.array([[1, 1], [2, 2], [3, 3]])
array([[1, 1],
       [2, 2],
       [3, 3]])
>>> np.insert(a, 1, 5)
array([1, 5, 1, ..., 2, 3, 3])

Insert simple element

>>> np.insert(a, 1, 5, axis=1)
array([[1, 5, 1],
       [2, 5, 2],
       [3, 5, 3]])

Insert sequence element

>>> np.insert(a, 1, [1, 2, 3], axis=1)
array([[1, 1, 1],
       [2, 2, 2],
       [3, 3, 3]])

>>> np.insert(a, 0, [5,5], axis=0)
array([[5, 5],
       [1, 1],
       [2, 2],
       [3, 3]])

Delete element

Delete the element of the specified dimension and location

>>> arr = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])

>>> np.delete(arr, 1, axis=0)  #Without changing the meta array, the resulting array does not share memory with the original array
array([[ 1,  2,  3,  4],
       [ 9, 10, 11, 12]])

>>> np.delete(arr, [1,2], axis=1)
array([[ 1,  4],
       [ 5,  8],
       [ 9, 12]])

>>> np.delete(arr, slice(0,2), axis=1)  #Delete slice specified location
array([[ 3,  4],
       [ 7,  8],
       [11, 12]])
>>> np.delete(arr, np.s_[:2], axis=1)  #np.s_ You can use: to represent slice syntax
array([[ 3,  4],
       [ 7,  8],
       [11, 12]])

Delete zeros at the beginning and end of a vector

>>> a = np.array([0, 0, 0, 1, 2, 3, 0, 2, 1, 0])
>>> np.trim_zeros(a)
array([1, 2, 3, 0, 2, 1])

>>> a=np.array([[0],[1]])
>>> np.trim_zeros(a)
array([[1]])

Remove duplicate numbers

Do not specify dimension

>>> np.unique([1, 1, 2, 2, 3, 3])
array([1, 2, 3])

>>> a = np.array([[1, 1], [2, 3]])
>>> np.unique(a)
array([1, 2, 3])

Specify dimension

>>> a = np.array([[1, 0, 0], [1, 0, 0], [2, 3, 4]])
>>> np.unique(a, axis=0)
array([[1, 0, 0], [2, 3, 4]])

Returns the index (the index of the first occurrence of each element)

>>> a = np.array([0,0,1,1,2,2])
>>> b,idx = np.unique(a, return_index=True)
>>> b
array([0, 1, 2])
>>> idx      #b is equal to a[idx]
array([0, 2, 4], dtype=int64)

Returns the reverse index.

Returns the index idx of the output unique value array out, so that out[idx] can get the original array. So IDX usually has duplicate values

>>> a = np.array([0,0,1,1,2,2])
>>> b,idx = np.unique(a, return_inverse=True)
>>> b
array([0, 1, 2])
>>> idx     #b[idx] is equal to a
array([0, 0, 1, 1, 2, 2], dtype=int64)

Returns the number of duplicate elements

>>> a = np.array([1, 2, 6, 4, 2, 3, 2])
>>> values, counts = np.unique(a, return_counts=True)
>>> values
array([1, 2, 3, 4, 6])
>>> counts
array([1, 3, 1, 1, 1])

Personal summary, some contents have been simply processed and summarized. If there is any fallacy, I hope you can point out it,
Continuous revision and update.

For revision history, see: https://github.com/hustlei/AI_Learning_MindMap