Weight segment tree, also known as chairman tree.
Weight segment tree, each leaf node represents a weight.
Each node has a weight, which represents the number of numbers in the current interval.
with This question For example, the data is 1 5 2 6 3 7 4, indicating the array to be queried a [].

Discretization
Discretization is to change the distance between all data into 1 with key value pairs.
For example, 1008 9 2 3 data sets can be numbered:
map[1]=2;map[2]=3;map[3]=9;map[4]=1008
The premise is to sort and de duplicate the original array.

//If my dataset exists in < vector >
sort(d.begin(),d.end());//sort
d.erase(unique(d.begin(),d.end()),d.end());//duplicate removal

In this way, the subscript of our vector is the key, and what is stored in it is the value.

Build weight segment tree
root[i] = [1,i] the root node of the weight segment tree of the interval
Because I and i-1 only differ by one value a[i] to build a tree, we can find which interval (node) weights need to be added by one through bisection on the premise of building [1,i-1]. Because our tree is built on the basis of subscripts, we first use low according to the discretized vector array d_ Bound () finds the subscript of a[i], searches the intervals of the tree according to the subscript, and updates the weight of each searched node until the leaf node.

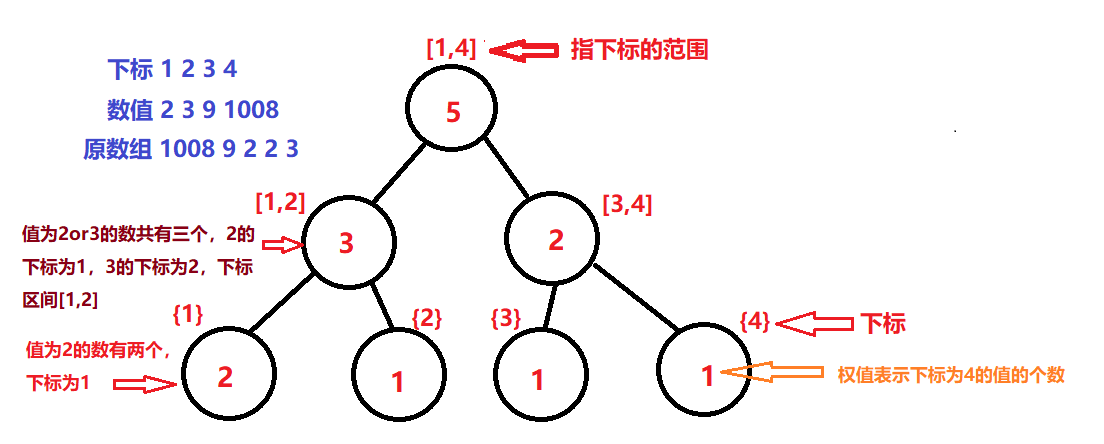
The tree building process is shown in the figure above, and the process of updating points is shown in the figure below:

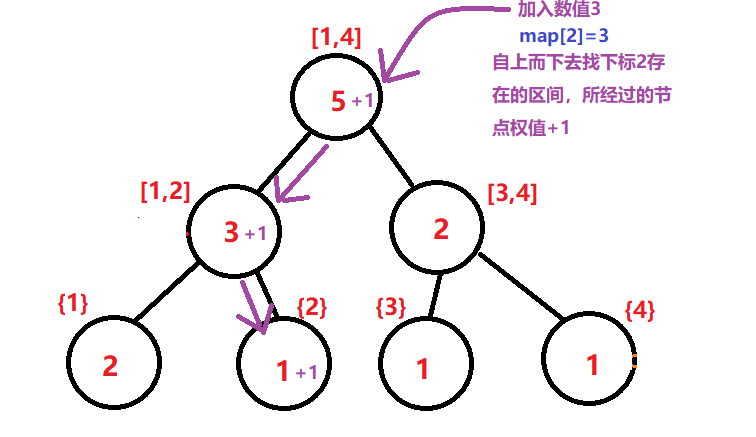
Add: because it is a point update, it is not necessary to build a tree at the beginning, because the weight of each point is 0 at the beginning, and the first value can be updated directly on this basis.

Code supplementary understanding
int p=tr[tr[now].l].val-tr[tr[pre].l].val; Calculate the number of numbers on the left half
if(k<=p) return query(tr[now].l,tr[pre].l,l,mid,k); If the number of the left half is more than k, then the number k smaller must be in the left interval.
else return query(tr[now].r,tr[pre].r,mid+1,r,k-p); If the number of the left half is less than k, then the number k smaller must be found in the interval on the right.
Until l=r, the value of l or r is the subscript of the k-th smallest number in the query interval.

#include<bits/stdc++.h>
using namespace std;
const int N=100010;
int n,m,a[N];
vector<int> d;
int root[N],tot;
struct SegTree{
    int l,r,val;
}tr[N*21];
int find(int x){
    return lower_bound(d.begin(),d.end(),x)-d.begin();
}
int build(int l,int r){
    int p=++tot;
    if(l==r) return p;
    int mid=(l+r)>>1;
    tr[p].l=build(l,mid);
    tr[p].r=build(mid+1,r);
    return p;
}
int update(int pre,int l,int r,int val){
    int p=++tot;
    tr[p]=tr[pre];
    tr[p].val++;
    int mid=(l+r)>>1;
    if(l<r){
        if(val<=mid) tr[p].l=update(tr[pre].l,l,mid,val);
        else tr[p].r=update(tr[pre].r,mid+1,r,val);
    }
    return p;
}
int query(int now,int pre,int l,int r,int k){
    if(l==r) return r;
    int p=tr[tr[now].l].val-tr[tr[pre].l].val;//Contraposition subtraction
    int mid=(l+r)>>1;
    if(k<=p) return query(tr[now].l,tr[pre].l,l,mid,k);
    else return query(tr[now].r,tr[pre].r,mid+1,r,k-p);
}
int main(){
    ios::sync_with_stdio(false);
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        d.push_back(a[i]);
    }
    sort(d.begin(),d.end());
    d.erase(unique(d.begin(),d.end()),d.end());
    int len=d.size();
    root[0]=build(0,len-1);
    for(int i=1;i<=n;i++){
        root[i]=update(root[i-1],0,len-1,find(a[i]));
    }
    while(m--){
        int l,r,k;
        cin>>l>>r>>k;
        int idx=query(root[r],root[l-1],0,len-1,k);
        cout<<d[idx]<<endl;
    }
    return 0;
}