subject

A pay cable television network plans to broadcast an important football game. Their relay network and user terminals form a tree structure. The root node of the tree is located at the scene of the football game, the leaves are each user terminal, and other transfer stations are the internal nodes of the tree.
The signal transmission cost from the relay station to the relay station and from the relay station to all user terminals is known, and the total cost of a broadcast is equal to the total cost of the transmitted signal.
Now each user has prepared a fee. If they want to watch this wonderful football game, the cable TV network has the right to decide which users to provide signals instead of which users to provide signals.
Write a program to find a scheme to make the cable TV network watch as many users as possible without losing money.

input

The first line of the input file contains two integers \ (N \) and \ (m \) separated by spaces, where \ (2 ≤ N ≤ 3000, 1 ≤ m ≤ N-1 \), \ (N \) is the total number of nodes of the whole cable TV network, and \ (M \) is the number of user terminals.
The first relay station, i.e. the root node number of the tree is \ (1 \), the other relay stations are \ (2 \) to \ (N-M \), and the user terminal numbers are \ (N-M+1 \) to \ (N \).
The following \ (N-M \) lines represent the data of one relay station, and the \ (i+1 \) line represents the data of the \ (i \) relay station. The format is as follows:
\(K\ A_1\ C_1\ A_2\ C_2\ \cdots \ A_k\ C_k\)
\(K \) indicates that the relay station is connected with \ (K \) nodes (relay station or user), and each node corresponds to A pair of integers \ (A \) and \ (C \), \ (A \) indicates the node number, and \ (C \) indicates the cost of transmitting signals from the current relay station to node \ (A \).
The last line in turn represents the amount of money all users are prepared to pay to watch the game.

output

The output file has only one line and contains an integer representing the maximum number of users required by the above problem.

sample input

5 3
2 2 2 5 3
2 3 2 4 3
3 4 2

sample output

2

Example explanation

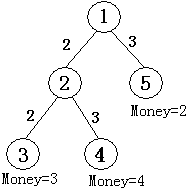
As shown in the figure above, there are five nodes in total. Node \ (① \) is the root node, i.e. the live broadcast station, \ (② \) is a transit station, \ (③ ④ ⑤ \) is the client, with a total of \ (M \) numbers from \ (N-M+1 \) to \ (N \), and the money they prepare for watching the game is \ (3, 4, 2 \), from node \ (① \) can transmit signals to node \ (② \), the fee is \ (2 \), and can also transmit signals to node \ (⑤ \), The cost is \ (3 \) (shown in the second line of data). Signals can be transmitted from node \ (② \) to node \ (③ \), and the cost is \ (2 \). The signal can also be transmitted to node \ (④ \), and the cost is \ (3 \) (as shown in the third line of data). If all users \ ((③ ④ ⑤) \) want to watch the game, the total cost of signal transmission is:
\(2 + 3 + 2 + 3 = 10 \), which is greater than the total cost that users are willing to pay \ (3 + 4 + 2 = 9 \), the cable TV network will lose money, and only allowing \ (③ ④ \) two users to watch the game will not lose money.

Problem solution

Tree Backpack
Definition f[i][j] means that the subtree with I as the root meets the profitability of j users watching the ball game. The result is to find the maximum j in the case of f[i][j] > = 0.

Click to view the code

#include<bits/stdc++.h>
using namespace std;
const int N=3000+5;
struct edge{
	int u,v,w;
};
vector<edge> g[N];
int n,m, val[N],f[N][N],k,a,c,size[N];
void dfs(int u){
	f[u][0]=0; //Boundary, initial value 
	if(u>n-m){ //Leaf node, special treatment 
		f[u][1]=val[u];
		size[u]=1;
		return;	
	}
	for(int i=0;i<g[u].size();i++){  
		int v=g[u][i].v;
		int w=g[u][i].w;
		dfs(v);
		size[u]+=size[v];//Count the number of users under the subtree 
		for(int j=m;j>=0;j--){ //Tree Backpack 
			for(int k=0;k<=min(j,size[v]);k++){ //If there are at most size[v] users under the V subtree, k cannot be greater than size[v] 
				f[u][j]=max(f[u][j],f[u][j-k]+f[v][k]-w);//Select the subtree of v and subtract the transmission cost w 
			}
		}
	}
}
int main(){
	scanf("%d %d",&n,&m);
	for(int i=1;i<=n-m;i++){
		scanf("%d",&k);
		for(int j=1;j<=k;j++){
			scanf("%d %d",&a,&c);
			g[i].push_back((edge){i,a,c});
		}
	}
	for(int i=n-m+1;i<=n;i++){
		scanf("%d",&val[i]);
	}
	memset(f,~0x3f,sizeof(f));//Initialize to a minimum because there will be losses (negative numbers) 
	dfs(1);
	for(int i=m;i>=0;i--){//Find the maximum number of users that can be satisfied without loss 
		if(f[1][i]>=0){
			printf("%d",i);
			return 0;
		}
	}
}