preface

Segment tree on oi wiki

If there is any mistake, you are welcome to point it out.

Pre cheese

1. Sequential storage of binary tree

What is a segment tree?

Segment tree, English is \ (Segment\) \(tree \). It is a data structure, which mainly solves interval modification and interval query.

We use an example to introduce a segment tree.

Cited example:

Now give a sequence \ (a \) with a length of \ (n \) (\ (n\le 10^6 \)). Then there are \ (m \) (\ (m\le 10^6 \)) query operations. For each operation, there are two cases:

• 1 x y, which means adding \ (a_x \) to \ (Y \).

• 2 l r, this operation means to query the interval sum of the interval \ (l-r \) and output it.

For such a problem, it is not difficult to find that it is a single point modification, interval query problem. For this problem, we can solve it with data structures such as tree array, blocking and even to be modified. However, today's protagonist is the line segment tree, so let's introduce the line segment tree method of this topic.

Specific method of segment tree

Obviously, for the example just now, the idea of using violence or prefix sum will be stuck to \ (O(nm) \. In the worst case, we can't pass the problem. If we want to pass the problem, we almost have to be an algorithm within the time complexity of \ (O(nlogm) \) or \ (O(mlogn) \. Therefore, our line segment tree algorithm was born!

We can convert the interval from \ (1 \) to \ (n \) of \ (a \) sequence into two left and right intervals. For the convenience of the example, let's assume that now \ (n=5 \). Obviously, we can convert \ ([1,n] \) into interval \ ([1,2] \) and interval \ ([4,5] \). Now define the left and right intervals of an interval as the left and right children of the interval. For example, if the current interval is \ ([x,y] \), his left child is \ ([x,(x+y)/2] \) and his right child is \ ([(x+y)/2,y] \). It should be noted that if \ (x=y \), it is a leaf node, because this interval can no longer be divided.

Then we can now serialize a \ (n=5 \) into a tree.

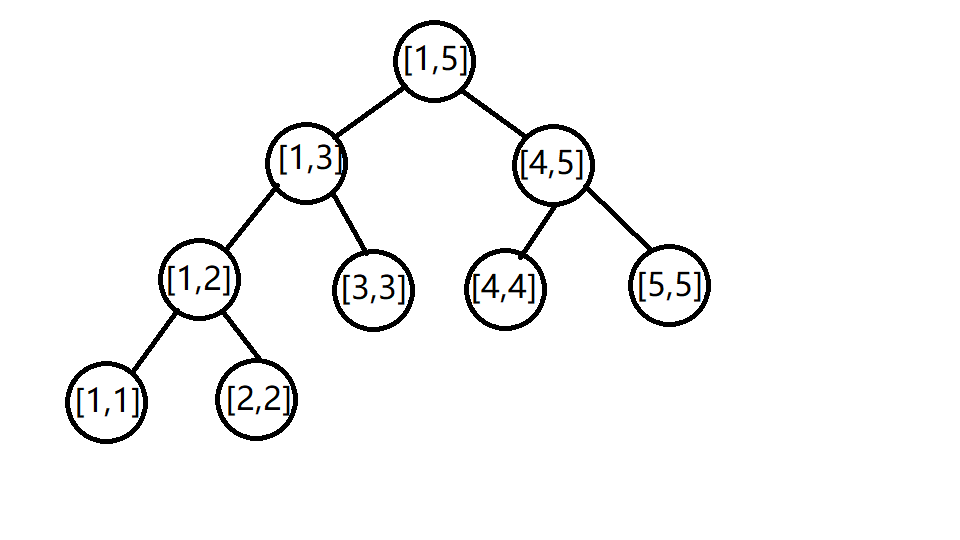
As shown in the figure, we can find that the left and right endpoints of the interval of all leaf nodes are equal. And because we need interval sum, we need to count the sum of each interval in the book. The interval number of the root node \ ([1,5] \) is \ (1 \), and the node number \ (x \) is \ (2x \) for its left son and \ (2x+1 \) for its right son through the sequential storage principle of binary tree. In order to easily query the left and right sons of an interval, we use this sequential storage principle to store the lesson tree.

We can use recursion to make achievements.

The reference code for tree building is as follows:

struct segmentree
{
	int l,r;//The left and right endpoints of the current node
	long long data;//The sum of the current interval
}tree[maxe];//Sequential storage, maxe means 4*n. (think carefully about why you drive 4x)
void build(int p,int l,int r)//p represents the node, l and R represent the right endpoint of the current node
{
	if(l==r)//If the left and right endpoints are equal, it indicates that this node is a leaf node and continues recursion with.
	{
   	  //Store the three information of the current node.
		tree[p].l=l;
		tree[p].r=r;
		tree[p].data=a[l];
		return;
	}
	int mid=(l+r)>>1;
   //Make achievements to his left and right sons
	build(p*2,l,mid);
	build(p*2+1,mid+1,r);
	tree[p].l=l,tree[p].r=r;
	tree[p].data=tree[p*2].data+tree[p*2+1].data;//Since there are left and right children in the current interval, the interval sum of the current interval is equal to the sum of the intervals of his left and right children.
}

After the tree is built, the next problem is the modification operation.

We can find that if the value at bit \ (x \) is modified, the interval sum of all intervals containing \ (x \) will change, that is, for a \ (n=5,x=3 \) tree, after \ (a_x \) is modified, we need to modify the interval sum of all orange marked intervals on the way.

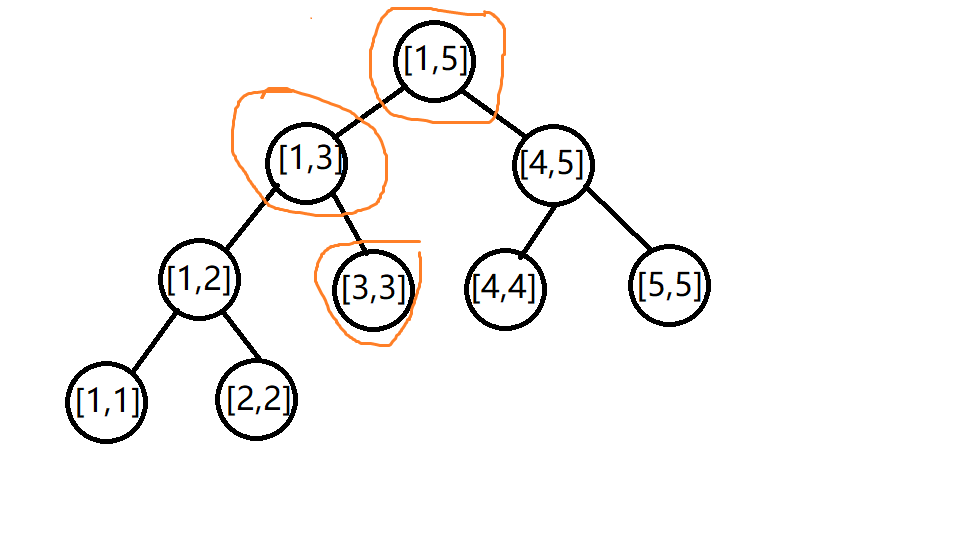
It can be found that no matter which digit you modify, the interval to be changed and the worst is \ ((logn+1) \) (rounded up) times, so the time complexity is \ (mlogn \).

For the code implementation of the modification operation, recursion is still used.

Modification operation reference code:

void change(int p,int x,int y)//p represents the node number currently recursive to, and X and Y represent changing a[x] to y
{
	if(tree[p].l>x||tree[p].r<x)//If the current interval of this node does not contain x, it does not need to be recursive.
	return;
	tree[p].data+=y;//If the current interval contains x, the interval sum of this interval should be added with y
  	 //Recursion of his children.
	change(p*2,x,y);
	change(p*2+1,x,y);

Finally, query interval and operation.

It is easy to find that if we want to query the interval sum of \ ([l,r] \) interval, we can find \ (logn \) maximum intervals in our split binary tree, and we only need to count the sum of all split intervals. The time complexity is still \ (O(mlogn) \).

Interval query reference code:

long long ask(int p,int l,int r)//p represents the current node number, l,r represents the [l,r] interval to query
{
	if(tree[p].r<l||tree[p].l>r)//If the currently enumerated interval does not intersect with the queried interval, it is not necessary to query
	return 0;
	if(tree[p].r<=r&&tree[p].l>=l)//If the interval to be queried contains the current American drama moral interval, we will directly return the interval sum of this interval
	{
		return tree[p].data;
	}
	long long res=0;
	res+=ask(p*2,l,r)+ask(p*2+1,l,r);//When you continue recursion, you should store the values obtained by recursion of its left and right children.
	return res;
}