On the boundary problem of dichotomy and two writing methods

We are familiar with the binary search method. For an ordered sequence, we can use the binary search method in O ( l o g N ) O(logN) O(logN) to find the desired element. However, in the process of code implementation, if you don't understand it carefully, the boundary conditions of dichotomy can sometimes be a headache, and the proper treatment of boundary conditions can reflect one's code skills, which is usually a point that the interviewer will pay close attention to. In addition, the dichotomy code in the boss's problem solution is always different in several small details, but the boss's code is no problem in how to measure, but he always has problems because some details are not handled well.

In fact, dichotomy usually has two implementation methods with slightly different details: left closed right closed and left closed right open. This paper will briefly introduce these two implementation methods, and point out their differences and application. I hope it can also help you fully understand dichotomy, and there will be no mistakes due to boundary conditions.

subject

Let's give the topic requirements first, and take the topic of a dichotomy on LeetCode as an example: 704. Binary search.

Given an n-element ordered (ascending) integer array nums and a target value target, write a function to search the target in nums. If the target value exists, return the subscript, otherwise return - 1.

Example 1:

Input: num = [- 1,0,3,5,9,12], target = 9
Output: 4
Explanation: 9 appears in nums with subscript 4

Example 2:

Input: num = [- 1,0,3,5,9,12], target = 2
Output: - 1
Explanation: 2 does not exist in nums, so - 1 is returned

Tips:

• You can assume that all elements in nums are not repeated.
• n will be between [1, 10000].
• Each element of num will be between [- 9999, 9999].

The given function signature (C + +) is as follows:

class Solution {
public:
    int search(vector<int>& nums, int target) {

    }
};

The following two sections are explained and referred to from [code Capriccio][ https://programmercarl.com/0704.%E4%BA%8C%E5%88%86%E6%9F%A5%E6%89%BE.html#%E6%80%9D%E8%B7%AF ].

Left closed right closed

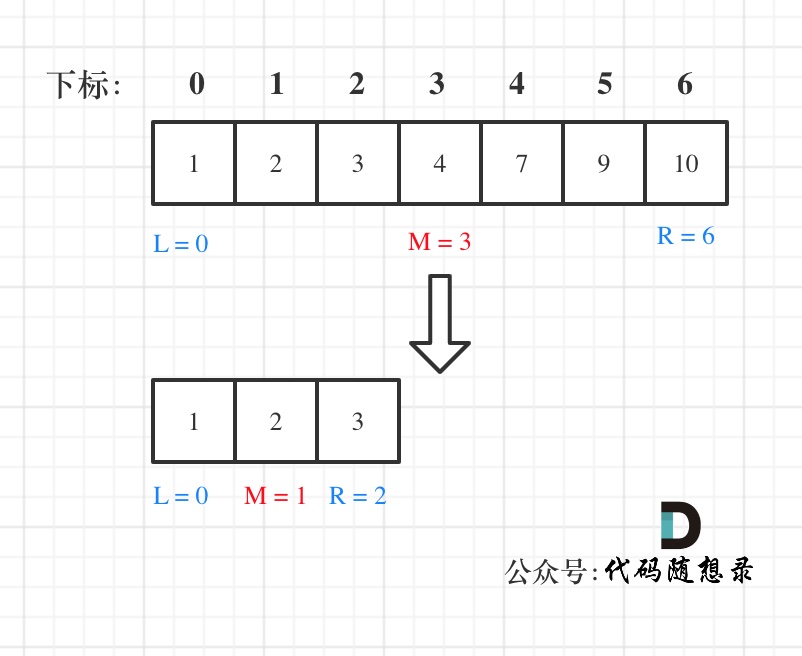
In the first way, we define that the target is in an interval closed on the left and closed on the right, that is [left, right] (this is very important, very important).

The definition of interval determines how to write the code of dichotomy. Because the target is defined in the [left, right] interval, there are the following two points:

• While (left < = right) use < =, because left == right is meaningful, so use<=
• If (Num [middle] > target) right should be assigned as middle - 1, because the current num [middle] must not be a target, then the end subscript position of the left interval to be found next is middle - 1

For example, find element 2 in the array: 1,2,3,4,7,9,10, as shown in the figure:

code:

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1; // Define that the target is in the left closed and right closed interval, [left, right]
        while (left <= right) { // When left==right, the interval [left, right] is still valid, so use<=
            int middle = left + ((right - left) / 2);// Preventing overflow is equivalent to (left + right)/2
            if (nums[middle] > target) {
                right = middle - 1; // target is in the left interval, so [left, middle - 1]
            } else if (nums[middle] < target) {
                left = middle + 1; // target is in the right range, so [middle + 1, right]
            } else { // nums[middle] == target
                return middle; // Find the target value in the array and return the subscript directly
            }
        }
        // Target value not found
        return -1;
    }
};

Left closed right open

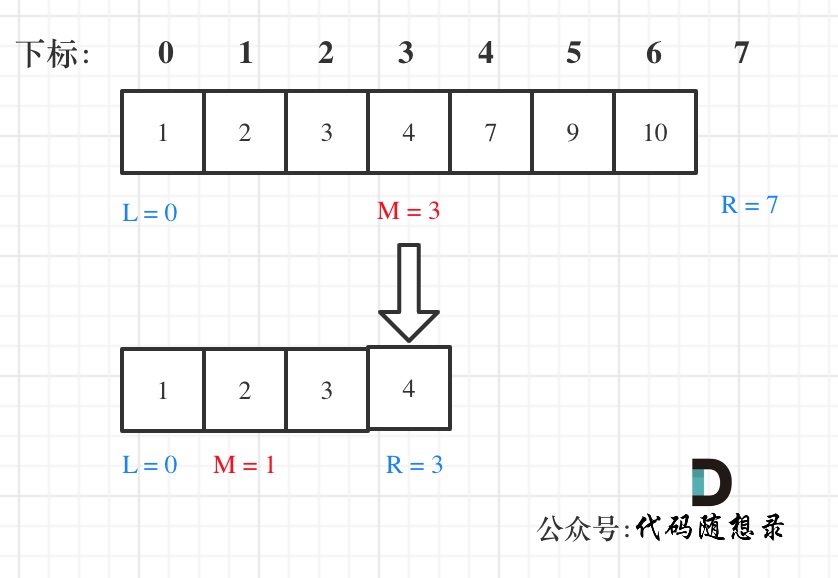
If the definition of target is in an interval that is closed on the left and open on the right, that is [left, right], the boundary treatment of dichotomy is quite different.

There are two points:

• While (left < right), use <, because left == right is meaningless in the interval [left, right)
• If (Num [middle] > target) right is updated to middle. Because the current num [middle] is not equal to the target, go to the left interval to continue the search, and the search interval is the left closed and right open interval, so right is updated to middle, that is, the next query interval will not compare num [middle]

Find element 2 in the array: 1,2,3,4,7,9,10, as shown in the figure: (note the difference between method 1 and method 1)

code:

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size(); // Define that the target is in the interval of left closing and right opening, that is: [left, right)
        while (left < right) { // Because when left == right, it is an invalid space in [left, right], so it is used<
            int middle = left + ((right - left) >> 1);
            if (nums[middle] > target) {
                right = middle; // target is in the left section, in [left, middle]
            } else if (nums[middle] < target) {
                left = middle + 1; // target is in the right section, in [middle + 1, right)
            } else { // nums[middle] == target
                return middle; // Find the target value in the array and return the subscript directly
            }
        }
        // Target value not found
        return -1;
    }
};

Search insertion location: maximum index not greater than target

In addition to searching, the dichotomy of the complete function should also return the position where the target should be inserted when the target element is not found, so as to facilitate the next possible insertion operation.

35. Search insertion position

Note that this problem requires to ensure that the given array is strictly single increment, that is, there are no equal elements. If there are equal elements, such as [1,2,3,3,5], there will be multiple reasonable insertion positions when inserting 3.

Version 1: left closed right closed

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int left = 0, right = nums.size() - 1;
        while (left <= right) {
            int mid = (right - left) / 2 + left;
            if (nums[mid] > target) right = mid - 1;
            else if (nums[mid] < target) left = mid + 1;
            else return mid;
        }
        return left;		// be careful
    }
};

Version 2: left closed right open

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int left = 0, right = nums.size();
        while (left < right) {
            int mid = (right - left) / 2 + left;
            if (nums[mid] > target) right = mid;
            else if (nums[mid] < target) left = mid + 1;
            else return mid;
        }
        return right;		// be careful
    }
};

Ref:

https://leetcode-cn.com/problems/binary-search

https://leetcode-cn.com/problems/search-insert-position/

https://programmercarl.com/0704.%E4%BA%8C%E5%88%86%E6%9F%A5%E6%89%BE.html#%E6%80%9D%E8%B7%AF