Recently, I have been learning data structures and algorithms. I deeply feel that our language learning is always just a tool, and the method is the most important part. In this article, I will illustrate the importance of algorithm, that is, the idea of writing program, in the program through several examples.

catalogue

1, Question 1 (print factorial)

Problem Description:

Problem analysis:

Solution:

2, Question 2 (compare polynomial calculation time)

Problem Description:

Problem analysis:

Solution:

 

1, Question 1 (print factorial)

Problem Description:

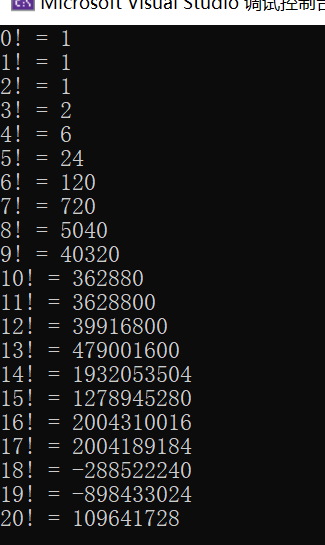
Print the factorial of number one to number 20

At first, I always print an extra 1, which annoys me very much, and since n equals 13, the data begins to overflow

 

Problem analysis:

Let's analyze the problem. There are two problems:

1. Print out one more 1

2. Data overflow

Solution:

1. Let's check the results and find that the problem is most likely that there is no loop itself during the loop

For (I = 1; I < num; I + +) / / this sentence is obviously wrong

Change to

for (i = 1; i <= num; i++) {//The value of i is multiplied by itself!
			n = n * i;
		}

 2. Here we will introduce a knowledge point of STL library in C + +

Conventional 32-bit integers can only handle numbers below 4 billion.
If you encounter a number larger than 4 billion, you need to use the 64 bit extension of C + +. Different compilers extend 64 bit integers differently. I also listen to other people's popular science. You can search in the station.

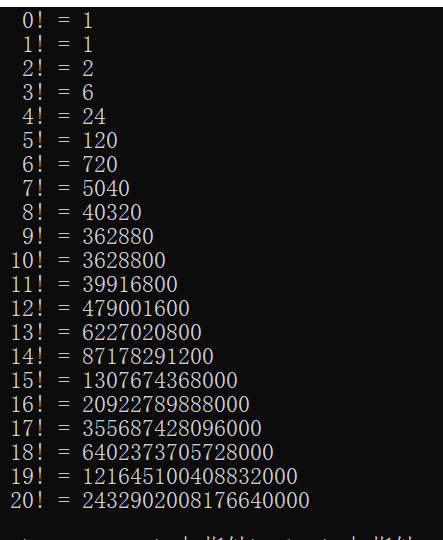
The optimized code is as follows:

#include <stdio.h>
void main() {
	__int64 fac(int num);
	int n = 1;
	int num;
	for (num = 0; num <= 20; ++num) {
		printf("%3d! = %I64d\n", num, fac(num));
	}
}
__int64 fac(int num) {
	register __int64 n = 1, i;     //register variable
		for (i = 1; i <= num; i++) {//The value of i is multiplied by itself!
			n = n * i;
		}
		return n;
}

2, Question 2 (compare polynomial calculation time)

Problem Description:

Here are some knowledge points in the test code:

This indicates that the program starts timing:

start = clock();

Timing at the end of this procedure:

stop = clock();

Clock tick: clock tick

CLK_TCK: the number of clock ticks taken by the machine clock per second

Problem analysis:

First, there are two algorithms for this problem:

Direct calculation

p1 += (pow(x, i)/i);

Take x as a common factor and put forward the calculation (Qin Jiushao method)

p2 = 1.0/(a[i - 1])+ (x*p2);

Then I found three problems:

1. Time cannot be measured

2. High program repeatability

3. The first result is inconsistent with the second result

Solution:

1. Let the measured function run repeatedly to make the measured total clock timing interval sufficiently long. Finally, calculate the measured function divided by the number of runs to obtain the average running time of each time

duration = ((double)(stop - start)) / CLK_TCK / MAXK;

2. You can set several more functions and call them to solve the problem

3. This is the problem of algorithm

This place is really error prone. I have changed it many times......

double f2(int n, double a[], double x) {
	int i;
	double p2 = 1.0/a[n];
	for (i = n; i > 0; i--) {
		p2 = 1.0/(a[i - 1])+ (x*p2);//There's something wrong with the algorithm (Mathematics)
	}
	return p2;
}

Overall Code:

#include <stdio.h>
#include <math.h>
#include <time.h>
clock_t start, stop;
double duration;
#define MAXN 101 / / the number of elements in the array (coefficients of polynomials). If you look at the value of n, you need to subtract one because there is a0
#define MAXK 1000 / / number of repeated calls
double f1(int n, double a[], double x)
{
	double p1 = a[0];//a[0] has been calculated, and the cycle starts from 1
	for (int i = 1; i <= n; i++) {
		p1 += (pow(x, i)/i);
	}
	return p1;	
}
double f2(int n, double a[], double x) {
	int i;
	double p2 = 1.0/a[n];
	for (i = n; i > 0; i--) {
		p2 = 1.0/(a[i - 1])+ (x*p2);//There's something wrong with the algorithm (Mathematics)
	}
	return p2;
}
double ceshijian()
{
	stop = clock();//Stop timing
	duration = ((double)(stop - start)) / CLK_TCK / MAXK;//Calculate single run time
	printf("ticks=%f\n", (double)(stop - start));
	printf("duration=%6.2e\n", duration);
	return 0;
}
int main()
{
	int i;
	double a[MAXN];
	for (i = 0; i < MAXN; i++) {
		a[i] = (double)i;
	}//The input is already the i value
	a[0] = 1;
	//Preparations that are not within the scope of the test are written before the clock() call
	start = clock();//Start timing
	for (int i = 0; i < MAXK; i++)//Repeat call
		f1(MAXN - 1, a, 1.1);//For the function under test, if you write an array here, it will be out of bounds, and it is uncertain to call a value. You can only write a, because the value to be defined is a
	printf("The first result is%f\n", f1(MAXN - 1, a, 1.1));
	ceshijian();

	start = clock();//Start timing
	for (i = 0; i < MAXK; i++)
		f2(MAXN - 1, a, 1.1);//For the function under test, if you write an array here, it will be out of bounds, and it is uncertain to call a value
	printf("The second result is%f\n", f2(MAXN - 1, a, 1.1));
	ceshijian();
	return 0;
}

give the result as follows

 

Obviously, the running time of the second method is much shorter than that of the first method

Therefore, Qin Jiushao method is more superior

Algorithm is a step to calculate or solve problems. Using a reasonable algorithm can shorten the running time and make the results more accurate