Tip: after the article is written, the directory can be generated automatically. Please refer to the help document on the right for how to generate it
preface
The original intention of learning python is shown in the figure. Then the boss of Tsinghua University recommended python to me. From then on, I started the road of learning by fishing for three days and drying the net for two days~
Before learning python, I found many small programs on the Internet. Due to the long history, I have forgotten where they came from. I added some comments to the code and slightly modified it to make the code more readable. If there is infringement, I will delete it immediately~
1, Falling Ginkgo
Quote an undergraduate teacher: "cherry blossoms are the most beautiful when they are half in the air and half in the tree. The space is the most beautiful when they are half in the air and half in the tree; the artistic conception is the most beautiful when you can take your favorite people to see them together at your age."
Therefore, we will use python's turtle library to complete the painting of Ginkgo biloba half in the air and half in the tree~
2, Code part
1. Import the required library
import turtle import random from math import *
2. Generate Fibonacci sequence
Fibonacci sequence refers to a sequence in which the sum of the first two terms is equal to the latter, for example [0 1 1 2 4 6 10]. Here, two functions are used to generate Fibonacci sequence.
def Fibonacci_Recursion_tool(n): #Fibonacci sequence method
if n <= 0:
return 0
elif n == 1:
return 1
else:
return Fibonacci_Recursion_tool(n - 1) + Fibonacci_Recursion_tool(n - 2)
def Fibonacci_Recursion(n): #Generate Fibonacci sequence and store it in the list
result_list = []
for i in range(1, n + 3):
result_list.append(Fibonacci_Recursion_tool(i))
return result_list
Call the function to generate a sequence as follows:
yu = Fibonacci_Recursion(top) #Generate Fibonacci sequence print(yu)
The operation results are as follows:

3. Define the method of generating leaves
def leaf(x, y, node):#Define how to draw leaves
til = turtle.heading()
i = random.random()
an = random.randint(10, 180)
ye = random.randint(6, 9)/10
turtle.color(ye, ye*0.9, 0)
turtle.fillcolor(ye+0.1, ye+0.05, 0)
turtle.pensize(1)
turtle.pendown()
turtle.setheading(an + 90)
turtle.forward(8*i)
px = turtle.xcor()
py = turtle.ycor()
turtle.begin_fill()
turtle.circle(7.5*i, 120) # Draw a 120 degree arc
turtle.penup() # Lift your pen
turtle.goto(px, py) # Return to dot position
turtle.setheading(an + 90) # Draw up
turtle.pendown() # Write and start painting
turtle.circle(-7.5*i, 120) # Draw a 120 degree arc
turtle.setheading(an + 100)
turtle.circle(10.5*i, 150)
turtle.end_fill() # Draw a 150 degree arc
turtle.penup()
turtle.goto(x, y)
turtle.setheading(til)
turtle.pensize(node / 2 + 1)
4. Method of defining spanning tree
Here, use X to generate random numbers, and use the if condition to judge whether to continue to draw branches and leaves, so as to make the tree more natural, irregular and better look. This will lead to different trees every time you run. I have added notes to the specific details. If you want to adjust the proportion of leaves in the air and the bifurcation degree of the tree, you can modify the x value range in the if judgment statement to increase or decrease the probability. As for how to achieve the perfect effect in your heart, you should try it slowly.
def draw(node, length, level, yu, button): #Define how to draw a tree
turtle.pendown()
t = cos(radians(turtle.heading()+5)) / 8 + 0.25
turtle.pencolor(t*1.6, t*1.2, t*1.4) #(r, g, b) RGB value corresponding to color
turtle.pensize(node/1.2) #Brush size
x = random.randint(0, 10) #Generate random numbers to decide whether to draw branches or falling leaves
if level == top and x > 6: #At this time, draw falling leaves. If the x range is too large, the tree will be too bald
turtle.forward(length) # Draw branches
yu[level] = yu[level] - 1
c = random.randint(2, 10)
for i in range(1, c):
leaf(turtle.xcor(), turtle.ycor(), node)
# Add 0.3x falling leaves
if random.random() > 0.3:
turtle.penup()
# Fall
t1 = turtle.heading()
an1 = -40 + random.random() * 40
turtle.setheading(an1)
dis = int(800 * random.random() * 0.5 + 400 * random.random() * 0.3 + 200 * random.random() * 0.2)
turtle.forward(dis)
turtle.setheading(t1)
turtle.right(90)
# Draw leaves
leaf(turtle.xcor(), turtle.ycor(), node)
turtle.left(90)
# return
t2 = turtle.heading()
turtle.setheading(an1)
turtle.backward(dis)
turtle.setheading(t2)
elif level==top and x < 7 : #At this time, draw branches and leaves. The x range is too large, resulting in too few falling leaves
turtle.penup()
turtle.forward(length)
elif level>3 and (x>6) :#Above the third level branches, there is a 40% probability to implement the following strategies
turtle.pendown()
turtle.forward(length)
c = random.randint(4, 6)
for i in range(3, c):
leaf(turtle.xcor(), turtle.ycor(),node)
leaf(turtle.xcor(), turtle.ycor(),node)
button=1# jump"""
else:
turtle.forward(length) # Draw branches
yu[level] = yu[level] -1
if node > 0 and button == 0:
# Calculate the deflection angle of the right branch, and add a random offset at the fixed angle deflection
right = random.random() * 5 + 17
# The deflection of the left branch is increased by a fixed angle
left = random.random() * 20 + 19
# Calculate the length of the next branch
child_length = length * (random.random() * 0.25 + 0.7)
# Turn right at an angle and draw the right branch
r=random.randint(0, 1)
if r==1:
turtle.right(right)
level = level + 1
#print("level", level)
else:
turtle.left(right)
level = level + 1
#print("level", level)
draw(node - 1, child_length,level,yu,button)
yu[level] = yu[level] +1
if yu[level] > 1:
# Turn left at an angle and draw the left branch
if r==1:
turtle.left(right + left)
draw(node - 1, child_length, level, yu,button)
# Turn the deflection angle back
turtle.right(left)
yu[level] = yu[level] - 1
else:
turtle.right(right + left)
draw(node - 1, child_length, level, yu,button)
# Turn the deflection angle back
turtle.left(left)
yu[level] = yu[level] - 1
else:
if r==1:
turtle.left(right + left)
turtle.right(left)
else:
turtle.right(right + left)
turtle.left(left)
turtle.penup()
#Return to the top of the previous node
turtle.backward(length)
5. Main function
Just call the above functions directly in the main function. top controls the height of the tree, and turn Speed controls the speed of the painting, and the final turn Write () is used to write the bottom signature.
if __name__ == '__main__':
turtle.setup(width=1.0, height=1.0) #Set full screen display
turtle.hideturtle() # Hide turtle
turtle.speed(0) # Set the speed of brush movement. The smaller the value of 0-10, the faster the speed
# turtle.tracer(0,0) #The switch and delay for animation are both 0
turtle.penup() # Lift the brush
turtle.left(90) # The default direction is the positive direction of the x-axis, and 90 degrees to the left is upward
turtle.backward(300) # Set the position of the turtle and move it down 300
top = 9 #Tree height
yu = Fibonacci_Recursion(top) #Generate Fibonacci sequence
yu.remove(yu[0])
#print(yu) print Fibonacci series
button = 0
draw(top, 120, 0, yu, button) # Call the function to start drawing
turtle.write(" wsw", font=("Microsoft YaHei ", 14, "normal")) #Generate signature
turtle.done()
3, Result display
After running the program, "turtle" will help you draw the whole tree. You just need to look at it and draw it. You need to wait for a certain time. The speed of painting can be selected by yourself. The final finished product is as follows, which is the feeling that half of the leaves you want are in the air. Ha ha ha~
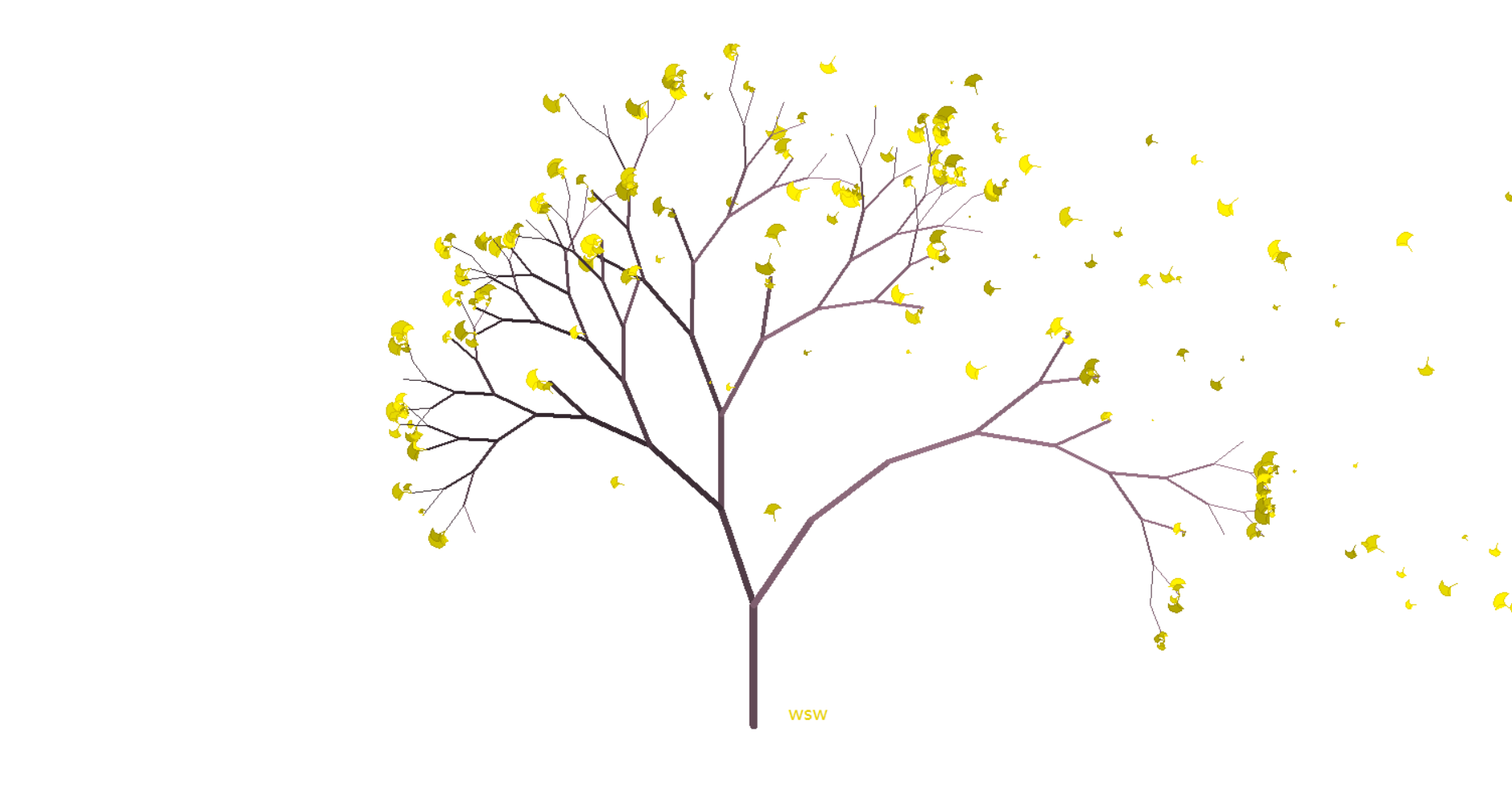
The above is the whole content of this small program. Although it's simple, it's still very interesting. Go and draw a tree for the ta you appreciate. At the most beautiful age, watch the petals flying in the air with the people you like~
The first in the series of useless python applet, which will be updated from time to time. The applet mentioned at the beginning, which automatically sends messages and warm reminders, has barely been realized. hhhh, the purpose of learning python as a beginner has been completed. In fact, this program is also very simple. It will be updated later when there is time.
The complete code will be uploaded to github later.