Topic overview

The game club, as its name suggests, is a club composed of several small games. When players enter the club, they will get a list of games, listing the n small games open in the club today, of which the i small game must be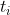Complete within time (assuming that the player enters the club at time 0, it only takes one unit time to start playing a game, excluding reading the game list and walking time on the road of the club), otherwise, it will be deducted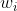Points of honor.

Every day, the club will award commemorative medals to the best order selector, the so-called best order, that is, the player with the least points deducted in the end.

Xiao Ming really wants a commemorative medal, so how to design the optimal order?

Input / output Description:

This topic is multiple groups of test data. Enter a positive integer in the first line T(1 <= T <= 1000)，Represents the number of test data groups;
For each set of data, enter a positive integer in the first row n(1 <= n <= 1000)，Represents the number of Games open today.

Example 1:

Input:
1
3
3 1 1
3 6 9

Output:
6

explain:
First complete game 3. At this time, if game 2 is not completed within the specified time, 6 points will be deducted; Then just finish Game 1 before time 3.
For this arrangement, only 6 points need to be deducted.

Problem solving ideas

First of all, I think of two general ideas, one is greed, the other is dynamic programming. First consider dynamic programming, that is, whether the optimal subproblem can be constructed. I find that this seems unrealistic... For example, the following example 1:

1
4
1 3   3  2
5 100 10 1

Assuming that we use one-dimensional dp, the subproblem constructed is that in the case of optimal ranking in the first I unit time, the minimum deduction score is dp[i]. As you can see, dp[1] = 0, which means only playing the first game; dp[2] = 0, that is, the first unit time plays the first game and the second unit time plays the second game; dp[3] = 1, that is, the first unit of time plays the first game, the second and third units of time play the third and fourth games respectively, and do not play the second game. In this case, dp[3] does not contain dp[2] and dp[1], that is to say, the dp we build in this way is problematic.

Then I thought, can we solve the problem through greedy methods. The initial solution is: first sort from small to large according to the chronological order, then sort from large to small according to the deduction cost, and then select the sorted games in turn. The problem with this approach is that if there is a costly game in the back, we only focus on the game to be completed in front of us, but fail to consider the game in the future, which will cause a great total cost (such as example 1 above).

Since the greed of positive order can't work, I'll reverse it. Let's first sort out the deadline of all games and find out the latest deadline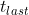, and then arrange the games to be played from the back to the front. stay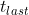At the moment, the game we choose should be the one that can minimize the deduction of glory points, that is, the deadline is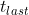The game with the most points deducted. By analogy, at the i-th moment, the scope of the game we play is: the deadline is from the i-th moment to the end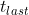All games at the moment (excluding those already played). In other words, we need to dynamically update the game cost order in the current to be played game list and select the largest one. Here I use heap implementation, which can achieve the time complexity of O(n log(n)).

Algorithm performance

The time complexity is O(n log(n)), and the space complexity is O(n).

Sample code

#include<iostream>
#include<algorithm>
#include<queue>
#include<vector>

#define NUM 1000

using namespace std;

bool cmp(pair<int, int> a, pair<int, int> b)
{
	if (a.first < b.first)
		return false;
	else if (a.first == b.first)
		return a.second < b.second;
	return true;
}

int main()
{
	int N, res;
	cin >> N;
	for (int ni = 0; ni < N; ++ni)
	{
		int Ng;
		res = 0;
		cin >> Ng;
		int *time_ddl = new int[Ng];
		int *time_pen = new int[Ng];
		for (int gi = 0; gi < Ng; ++gi)
			cin >> time_ddl[gi];
		for (int gi = 0; gi < Ng; ++gi)
		{
			cin >> time_pen[gi];
			res += time_pen[gi];
		}

		vector<pair<int, int>> time_sort;
		for (int gi = 0; gi < Ng; ++gi)
			time_sort.push_back(pair<int, int> {time_ddl[gi], time_pen[gi]});
		sort(time_sort.begin(), time_sort.end(), cmp);

		int pc = time_sort.front().first;
		priority_queue<int, vector<int>, less<int>> pen;
		for (auto idx = time_sort.begin(); idx != time_sort.end();)
		{
			if (pc == (*idx).first)
			{
				pen.push((*idx).second);
				idx++;
			}
			else
			{
				while (pc != (*idx).first)
				{
					if (pen.empty() == 0)
					{
						res -= pen.top();
						pen.pop();
					}
					pc--;
				}
			}
		}
		res -= pen.top();

		cout << res << endl;

		delete [] time_ddl;
		delete [] time_pen;
	}
}