OO design - JAVA rational number class design

problem

The rational number class is designed in an object-oriented manner according to the BigDecimal class.

Give your test code. A rational number class should be called in other classes with different classes of rational numbers.

Try to compare the answer with the rational number code of c language.

Rational functions

package test;

import java.math.BigDecimal;

public class Rational {
	private long numerator = 0; //molecule
	private long denominator = 1; //denominator
	public long getNumerator() {
		return numerator;
	}

	public void setNumerator(long numerator) {
		this.numerator = numerator;
	}

	public long getDenominator() {
		return denominator;
	}

	public void setDenominator(long denominator) {
		this.denominator = denominator;
	}

	public Rational(){//Numerator denominator initialization
		this.numerator = 0;
		this.denominator = 1;
	}

	public Rational(long numerator, long denominator){
		this.numerator = numerator/gcd(Math.abs(numerator), Math.abs(denominator)); //Molecular reduction (divided by the maximum common divisor of numerator and denominator)
		this.denominator = denominator/gcd(Math.abs(numerator), Math.abs(denominator));//Denominator reduction (divided by the maximum common divisor of numerator and denominator)
	}

	public static long gcd (long number1, long number2){//Maximum common divisor calculation
		while (number1 != number2)
		{
			if (number1 > number2)
				number1 = number1 - number2;
			else
				number2 = number2 - number1;
		}
		return number1;
	}
	public static Rational add (Rational num1, Rational num2) {//Sum of rational numbers
		long tempNumerator = num1.numerator*num2.denominator + num1.denominator*num2.numerator;
		long tempDenominator = num1.denominator*num2.denominator;
		long gcd = gcd(Math.abs(tempNumerator),Math.abs(tempDenominator));
		Rational rationalNumber = new Rational(tempNumerator/gcd,tempDenominator/gcd);
		return rationalNumber;
	}

	public static Rational subtract (Rational num1, Rational num2) {//Rational number difference
		long tempNumerator = num1.numerator*num2.denominator - num1.denominator*num2.numerator;
		long tempDenominator = num1.denominator*num2.denominator;
		long gcd = gcd(Math.abs(tempNumerator),Math.abs(tempDenominator));
		Rational rationalNumber = new Rational(tempNumerator/gcd,tempDenominator/gcd);
		return rationalNumber;
	}

	public static Rational multiply (Rational num1, Rational num2) {//Rational number quadrature
		long tempNumerator = num1.numerator*num2.numerator;
		long tempDenominator = num1.denominator*num2.denominator;
		long gcd = gcd(Math.abs(tempNumerator),Math.abs(tempDenominator));
		Rational rationalNumber = new Rational(tempNumerator/gcd,tempDenominator/gcd);
		return rationalNumber;
	}

	public static Rational divide (Rational num1, Rational num2) {//Quotient of rational number
		long tempNumerator = num1.numerator*num2.denominator;
		long tempDenominator = num1.denominator*num2.numerator;
		long gcd = gcd(Math.abs(tempNumerator),Math.abs(tempDenominator));
		Rational rationalNumber = new Rational(tempNumerator/gcd,tempDenominator/gcd);
		return rationalNumber;
	}

}

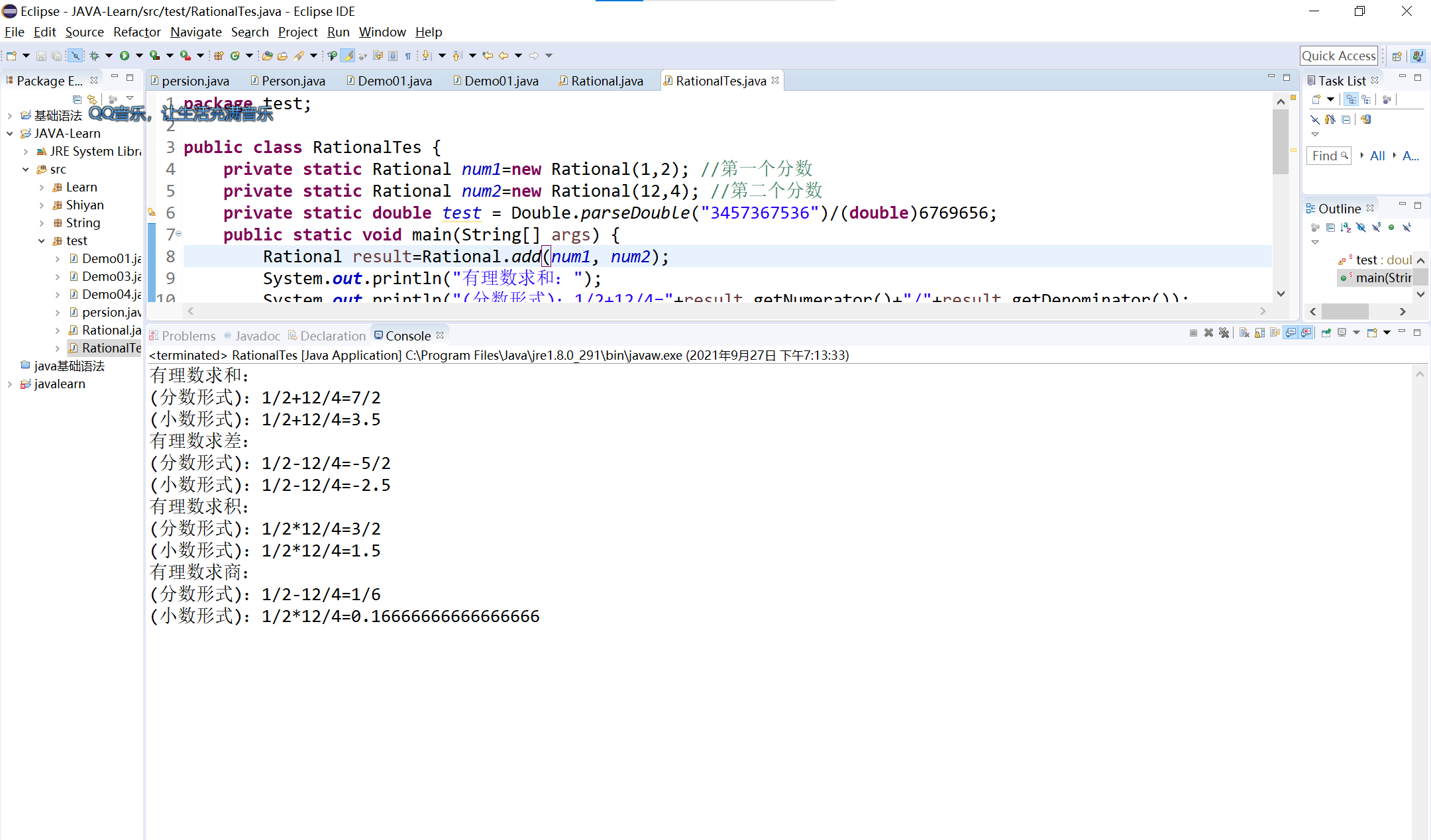
Test Class file

package test;

public class RationalTes {
	private static Rational num1=new Rational(1,2); //First score
	private static Rational num2=new Rational(12,4); //Second score
	private static double test = Double.parseDouble("3457367536")/(double)6769656;
	public static void main(String[] args) {
		Rational result=Rational.add(num1, num2);
		System.out.println("Sum of rational numbers:");
		System.out.println("(Fractional form): 1/2+12/4="+result.getNumerator()+"/"+result.getDenominator());
		System.out.println("(decimal form ): 1/2+12/4="+(result.getNumerator()/(double)result.getDenominator()));
		result=Rational.subtract(num1, num2);
    	System.out.println("Rational difference:");
		System.out.println("(Fractional form): 1/2-12/4="+result.getNumerator()+"/"+result.getDenominator());
		System.out.println("(decimal form ): 1/2-12/4="+(result.getNumerator()/(double)result.getDenominator()));
		result=Rational.multiply(num1, num2);
		System.out.println("Rational number quadrature:");
		System.out.println("(Fractional form): 1/2*12/4="+result.getNumerator()+"/"+result.getDenominator());
		System.out.println("(decimal form ): 1/2*12/4="+(result.getNumerator()/(double)result.getDenominator()));
		result=Rational.divide(num1, num2);
		System.out.println("Quotient of rational number:");
		System.out.println("(Fractional form): 1/2-12/4="+result.getNumerator()+"/"+result.getDenominator());
		System.out.println("(decimal form ): 1/2*12/4="+(result.getNumerator()/(double)result.getDenominator()));
	}

}

Operation results

Problem summary

Q1: where is it more object-oriented than C language?

A1: the process oriented of C language is to analyze the steps needed to solve the problem, and then use functions to solve it step by step. The Java language decomposes the problem transaction into various objects. The purpose of establishing objects is not to complete a step, but to describe the behavior of something in the whole problem-solving step. For example, in this code, data encapsulation is carried out for different objects, and all communication is realized through the method of objects.

Q2: how to use this code?

A2: download the package locally, import the package into the IDE, and call the function through "class name. Method". Use setter/getter to set and access private.

Q3: does the calling code depend on the properties of the rational number class? When the rational number class is modified, will it affect the call?

A3: the calling code depends on the properties of this class. When the rational number class is modified, it will affect the call.

Q4: Why are some methods set to private?

A4: set some methods to private in the following scenarios:

When a method wants to be used only by this class.

It has nothing to do with the internal state of this class.

The simplest example is the tool methods we often see. We want to create instances of classes without allocating memory, so we will declare them public static. On this basis, if we like that only this class can access this method, we can declare them private static.
--------
Copyright notice: This is the original article of CSDN blogger "weixin_39791653", which follows the CC 4.0 BY-SA copyright agreement. Please attach the original source link and this notice for reprint.
Original link: https://blog.csdn.net/weixin_39791653/article/details/114081133