Camera calibration
Camera calibration: in short, it is the process of obtaining camera parameters. Parameters such as camera internal parameter matrix, projection matrix, rotation matrix, translation matrix, etc
What are camera parameters?
Simply put, take a picture of people and things in the real world (two-dimensional). The relationship between the three-dimensional coordinates of people or things in the world and the corresponding two-dimensional coordinates on the image. What is used to express the relationship between two different dimensional coordinates? Use camera parameters.
Imaging principle of camera
Let's take a look at the imaging principle of the camera:
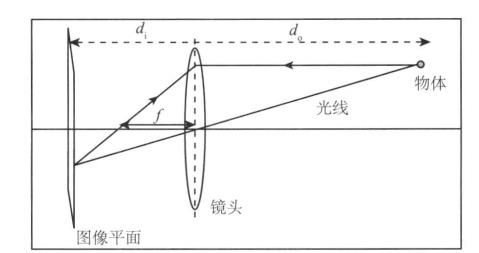
As shown in the figure, this is a camera model. Simplify the object as a point. The light from the object passes through the lens and hits the image plane (image sensor) for imaging. d0 is the distance from the object to the lens, di is the distance from the lens to the image plane, and f is the focal length of the lens. The three meet the following relationship.
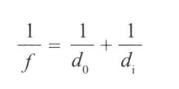
Now, simplify the camera model above.
The camera aperture is regarded as infinitesimal, and only the ray at the center is considered, so the influence of the lens is ignored. Then, since d0 is much larger than di, the image plane is placed at the focal length, so that the object is imaged as an inverted image on the image plane (without the influence of the lens, only the light entering from the central aperture is considered). This simplified model is the small hole camera model. Then, we can simply get a straight image (without Handstand) by placing the image plane in front of the lens at the focal distance. Of course, this is only theoretical. You can't take the image sensor out of the camera and put it in front of the lens. In practical application, the small hole camera should invert the imaged image to obtain an upright image.
So far, we have obtained a simplified model, as shown in the following figure:
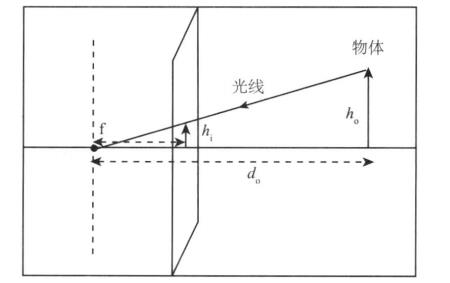
h0 is the height of the object, hi is the height of the object on the image, f is the focal length (distance), and d0 is the distance from the image to the lens. The four meet the following relationships:
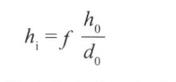
The height hi of the object in the image is inversely proportional to d0. In other words, the farther away from the lens, the smaller the object in the image, and the closer it is, the larger it is (well, this sentence is nonsense).
But through this formula, we can predict the position of objects in three dimensions in the image (two dimensions). So how do you predict?
Camera calibration
As shown in the figure below, according to the simplified model above, consider a point in the 3D world and its coordinate relationship in the image (2D).
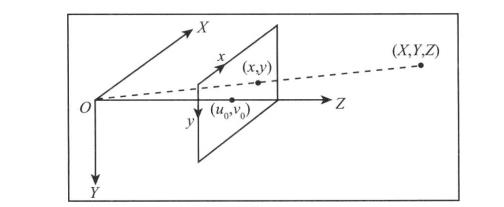
(x, y, Z) is the three-dimensional coordinate of the point, and (x, y) is its coordinate on the image (two-dimensional) after imaging through the camera. u0 and v0 are the center points (main points) of the camera, which are located at the center of the image plane (theoretically, but the actual camera will have a deviation of several pixels)
Now we only consider the y direction. Since we need to convert the coordinates in the three-dimensional world into pixels on the image (the coordinates on the image are actually the positions of pixels), we need to find the focal length in the y direction
Equal to how many pixels (the focal length is represented by the pixel value), Py represents the height of the pixel, and the focal length f (m or mm). The focal length represented by vertical pixels is
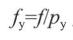
According to equation (1), only the Y direction is considered. We get the coordinates of point y in the three-dimensional world in the image (two-dimensional).
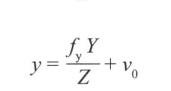
Similarly, we get the coordinates of x.
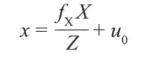
Now, move the origin O of the coordinate system in the above figure to the upper left corner of the image. Since (x, y) is an offset with respect to (u0, v0), the above formula representing the coordinates of the midpoint of the image (two-dimensional) remains unchanged. Rewrite the formula in the form of matrix to obtain.

Among them, the first matrix on the left of the equation is called "camera internal parameter matrix", and the second matrix is called (projection matrix).
More generally, the reference coordinate system at the beginning is not located at the main point (center point), so two additional parameters "rotation vector" and "translation vector" are required to represent this formula. These two parameters are different in different perspectives. After integration, the above formula is rewritten as.

Correction distortion
After the camera parameters are obtained through camera calibration, two mapping functions (x coordinate and y coordinate) can be calculated, which give the image coordinates without distortion respectively. The distorted image is remapped into an image without distortion.
code:
When doing camera calibration, generally take a group of images with the calibration board (chessboard), extract corners from these images, and calculate camera parameters through the coordinates of corners in the image and the coordinates in the three-dimensional world (usually customized three-dimensional coordinates).
1 std::vector<cv::Point2f>imageConers; 2 //Extract the corners of the calibration image and save the corner coordinates (two-dimensional) 3 cv::findChessboardCorners(image, 4 boardSize, //The number of corner points, such as (6,4) six rows and four columns 5 imageConers);
The function calibrateCamera completes camera calibration.
cv::calibrateCamera(objectPoints,//Three dimensional coordinates imagePoints, //Two dimensional coordinates imageSize,//Image size camerMatirx,//Camera intrinsic parameter matrix disCoeffs,//Projection matrix rvecs, //rotate tvecs,//translation flag //The opencv tag provides several parameters. Please refer to the online opencv document );
Calculate distortion parameters and remove distortion
//Calculate distortion parameters
cv::initUndistortRectifyMap(camerMatirx, disCoeffs,
cv::Mat(), cv::Mat(), image.size(), CV_32FC1,
map1, //x mapping function
map2 //y mapping function
);
//Application mapping function
cv::remap(image, //distorted image
undistorted, //De distorted image
map1, map2, cv::INTER_LINEAR);
Now integrate the code.
Example:
Header h
#include<opencv2\core\core.hpp>
#include<opencv2\highgui\highgui.hpp>
#include<opencv2\imgproc\imgproc.hpp>
#include<opencv2\calib3d\calib3d.hpp>
#include <opencv2/features2d/features2d.hpp>
#include<string>
#include<vector>
class CameraCalibrator
{
private:
//World coordinates
std::vector < std::vector<cv::Point3f >> objectPoints;
//Image coordinates
std::vector <std::vector<cv::Point2f>> imagePoints;
//Output matrix
cv::Mat camerMatirx;
cv::Mat disCoeffs;
//sign
int flag;
//De distortion parameters
cv::Mat map1, map2;
//Whether to remove distortion
bool mustInitUndistort;
///Save point data
void addPoints(const std::vector<cv::Point2f>&imageConers, const std::vector<cv::Point3f>&objectConers)
{
imagePoints.push_back(imageConers);
objectPoints.push_back(objectConers);
}
public:
CameraCalibrator() :flag(0), mustInitUndistort(true){}
//Open the chessboard picture and extract corners
int addChessboardPoints(const std::vector<std::string>&filelist,cv::Size &boardSize)
{
std::vector<cv::Point2f>imageConers;
std::vector<cv::Point3f>objectConers;
//Enter the world coordinates of the corner
for (int i = 0; i < boardSize.height; i++)
{
for (int j = 0; j < boardSize.width; j++)
{
objectConers.push_back(cv::Point3f(i, j, 0.0f));
}
}
//Calculate the coordinates of corners in the image
cv::Mat image;
int success = 0;
for (int i = 0; i < filelist.size(); i++)
{
image = cv::imread(filelist[i],0);
//Find corner coordinates
bool found = cv::findChessboardCorners(image, boardSize, imageConers);
cv::cornerSubPix(image,
imageConers,
cv::Size(5, 5),
cv::Size(-1, -1),
cv::TermCriteria(cv::TermCriteria::MAX_ITER + cv::TermCriteria::EPS,
30, 0.1));
if (imageConers.size() == boardSize.area())
{
addPoints(imageConers, objectConers);
success++;
}
//Draw corners
cv::drawChessboardCorners(image, boardSize, imageConers, found);
cv::imshow("Corners on Chessboard", image);
cv::waitKey(100);
}
return success;
}
//Camera calibration
double calibrate(cv::Size&imageSize)
{
mustInitUndistort = true;
std::vector<cv::Mat>rvecs, tvecs;
//Camera calibration
return cv::calibrateCamera(objectPoints, imagePoints, imageSize,
camerMatirx, disCoeffs, rvecs, tvecs, flag);
}
///De distortion
cv::Mat remap(const cv::Mat &image)
{
cv::Mat undistorted;
if (mustInitUndistort)
{
//Calculate distortion parameters
cv::initUndistortRectifyMap(camerMatirx, disCoeffs,
cv::Mat(), cv::Mat(), image.size(), CV_32FC1, map1, map2);
mustInitUndistort = false;
}
//Application mapping function
cv::remap(image, undistorted, map1, map2, cv::INTER_LINEAR);
return undistorted;
}
//Constant member function to obtain the data of camera internal parameter matrix and projection matrix
cv::Mat getCameraMatrix() const { return camerMatirx; }
cv::Mat getDistCoeffs() const { return disCoeffs; }
};
Source cpp
#include "header. h"
#include<iomanip>
#include<iostream>
int main()
{
CameraCalibrator Cc;
cv::Mat image;
std::vector<std::string> filelist;
cv::namedWindow("Image");
for (int i = 1; i <= 22; i++)
{
///Read picture
std::stringstream s;
s << "D:/images/chessboards/chessboard" << std::setw(2) << std::setfill('0') << i << ".jpg";
std::cout << s.str() << std::endl;
filelist.push_back(s.str());
image = cv::imread(s.str(),0);
cv::imshow("Image", image);
cv::waitKey(100);
}
//Camera calibration
cv::Size boardSize(6, 4);
Cc.addChessboardPoints(filelist, boardSize);
Cc.calibrate(image.size());
//De distortion
image = cv::imread(filelist[1]);
cv::Mat uImage=Cc.remap(image);
cv::imshow("Original image", image);
cv::imshow("De distortion", uImage);
//Display camera internal parameter matrix
cv::Mat cameraMatrix = Cc.getCameraMatrix();
std::cout << " Camera intrinsic: " << cameraMatrix.rows << "x" << cameraMatrix.cols << std::endl;
std::cout << cameraMatrix.at<double>(0, 0) << " " << cameraMatrix.at<double>(0, 1) << " " << cameraMatrix.at<double>(0, 2) << std::endl;
std::cout << cameraMatrix.at<double>(1, 0) << " " << cameraMatrix.at<double>(1, 1) << " " << cameraMatrix.at<double>(1, 2) << std::endl;
std::cout << cameraMatrix.at<double>(2, 0) << " " << cameraMatrix.at<double>(2, 1) << " " << cameraMatrix.at<double>(2, 2) << std::endl;
cv::waitKey(0);
}

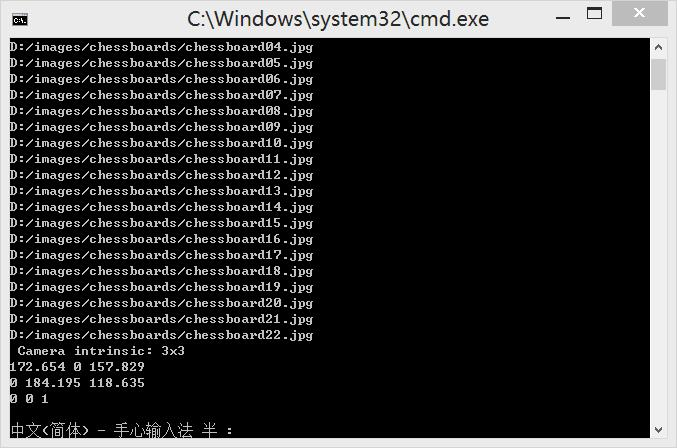
Look, the parameter matrix in the camera is
172.654 ,0,157.829
0,184.195,118.635
0 ,0 ,1