recursion
In short, recursion is a method that calls itself and passes in different variables each time. Recursion helps programmers solve complex problems and makes code concise.
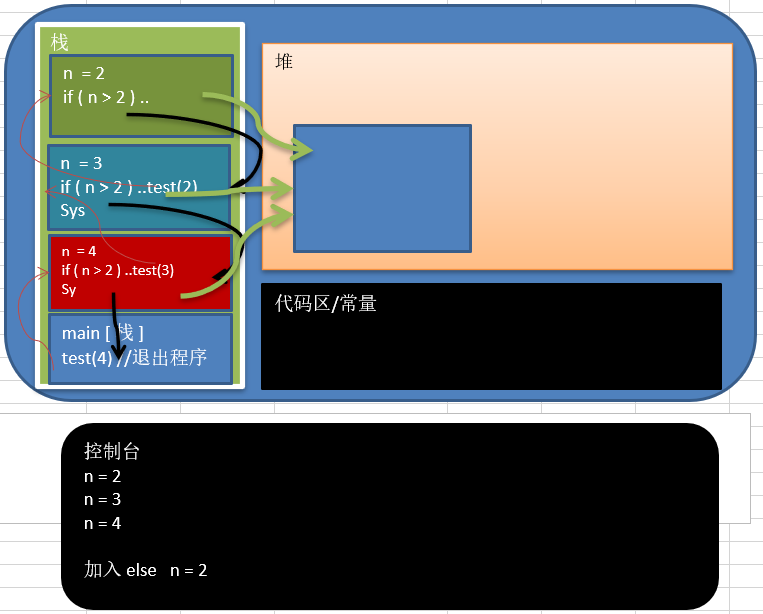
Recursive call mechanism
1) Printing problem 2) factorial problem
public class RecursionTest {
public static void main(String[] args) {
//print(4);
int res = factorial(3);
System.out.println(res);
}
//Print problem
public static void print(int n) {
if (n > 2) {
print(n - 1);
}
System.out.println("n="+n);
}
//Factorial problem
public static int factorial(int n) {
if (n == 1) {
return 1;
} else {
return factorial(n-1)*n;//1*2*3
}
}
}
Recursive call rule
1. When a program executes a method, it opens up a separate space (stack)
2. The data (local variables) of each space are independent
Problems that recursion can solve and rules to follow
Problems that can be solved
1. Various mathematical problems, such as: 8 queen problem, Hanoi Tower, factorial problem, maze problem, ball and basket problem (google programming competition)
2. Recursion is also used in various algorithms, such as fast sorting, merge sorting, binary search, divide and conquer algorithm, etc
3. The stack will be used to solve the problem - "recursion", the code is relatively concise
Rules to follow
1. When a method is executed, a new protected independent space (stack space) is created
2. The local variables of the method are independent and will not affect each other, such as n variables
3. If a reference type variable (such as an array) is used in the method, the data of the reference type will be shared
4. Recursion must approach the condition of exiting recursion, otherwise it is infinite recursion and StackOverflowError occurs
5. When a method is executed or encounters a return, it will return. Follow the rule that whoever calls will return the result to whom. At the same time, when the method is executed or returned, the method will also be executed.
Maze backtracking problem
Problem description
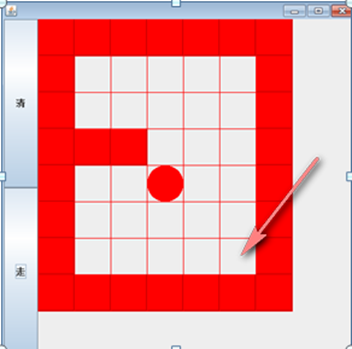
explain:
1. The path obtained by the ball is related to the path finding strategy set by the programmer, that is, the order of up, down, left and right
2. When getting the ball path again, you can first use (lower right, upper left), and then change it to (upper right, lower left) to see if the path has changed
3. Test backtracking phenomenon
Thinking: how to find the shortest path?
code implementation
public class MiGong {
public static void main(String[] args) {
//First create a two-dimensional array to simulate the maze map, and use 1 to represent the wall
int[][] map = new int[8][7];
//Set up and down to 1
for (int i = 0; i < 7; i++) {
map[0][i] = 1;
map[7][i] = 1;
}
//All left and right are set to 1
for (int i = 0; i < 8; i++) {
map[i][0] = 1;
map[i][6] = 1;
}
//Set baffle, 1 indicates
map[3][1] = 1;
map[3][2] = 1;
//map[1][2] = 1;// Block the road and observe the backtracking phenomenon
//map[2][2] = 1;// Block the road and observe the backtracking phenomenon
//Output map
System.out.println("Original map situation");
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
//Use recursive backtracking to find the way for the ball
setWay(map,1,1);
//setWay2(map,1,1);
//Export new map
System.out.println("The map of the ball passing by");
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
}
//A method of using recursive backtracking to find the way for a small ball
//explain
//1. Map represents a map
//2. i,j represents the coordinates of the starting position
//3. If the ball can reach the map[6][5], the path is found
//4. Convention: when map[i][j] is 0, it means that the point has not passed; 1 indicates the wall; Is 2, indicating the access road, which can be taken; A value of 3 indicates that the point has passed, but it is impossible
//5. When walking through the maze, you need to determine a strategy (method): down - > right - > up - > left. If you can't get through at a certain point, go back
/**
*
* @param map Maze map
* @param i Coordinates of the starting position
* @param j Coordinates of the starting position
* @return If the path is found, it returns true; otherwise, it returns false
*/
public static boolean setWay(int[][] map, int i, int j) {
if (map[6][5] == 2) {//The path has been found
return true;
} else {
if (map[i][j] == 0) {//If the current point has not passed
//According to the strategy, go down - > right - > up - > left
map[i][j] = 2;//It is assumed that this point can be accessed
if (setWay(map,i+1, j)) {//Go down
return true;
} else if (setWay(map, i,j+1)) {//turn right
return true;
}else if (setWay(map,i-1, j)) {//Go up
return true;
}else if (setWay(map, i,j-1)) {//turn left
return true;
} else {//It means that this point is impassable and dead end
map[i][j] = 3;
return false;
}
} else {//If map [i] [J]= 0, it may be 1,2,3
return false;
}
}
}
//Use recursive backtracking to find the way for the ball (modify the way finding strategy), and change it to up - > right - > down - > left
public static boolean setWay2(int[][] map, int i, int j) {
if (map[6][5] == 2) {//The path has been found
return true;
} else {
if (map[i][j] == 0) {//If the current point has not passed
//According to the strategy, go down - > right - > up - > left
map[i][j] = 2;//It is assumed that this point can be accessed
if (setWay2(map,i-1, j)) {//Go up
return true;
} else if (setWay2(map, i,j+1)) {//turn right
return true;
}else if (setWay2(map,i+1, j)) {//Go down
return true;
}else if (setWay2(map, i,j-1)) {//turn left
return true;
} else {//It means that this point is impassable and dead end
map[i][j] = 3;
return false;
}
} else {//If map [i] [J]= 0, it may be 1,2,3
return false;
}
}
}
}
Eight queens problem
Problem introduction and train of thought analysis

Question introduction:
The eight queens problem is an ancient and famous problem and a typical case of backtracking algorithm. The problem was put forward by international chess player Max Bethel in 1848 - in August × Eight queens are placed on the 8-grid chess so that they can't attack each other, that is, any two Queens can't be in the same row, column or slash. Ask how many kinds of pendulum methods there are.
Train of thought analysis:
1. The first queen puts the first row and the first column first
2. The second queen is placed in the first column of the second row, and then judge whether it is OK. If it is not OK, continue to put it in the second column and the third column, and put all the columns in turn to find a suitable position
3. Continue the third queen, or the first and second columns... Until the eighth queen can also be placed in a non conflict position, it can be regarded as finding a correct solution
4. When a correct solution is obtained, when the stack returns to the previous stack, it will start backtracking, that is, the first queen will get all the correct solutions put in the first column
5. Then go back and continue to put the first queen in the second column, and then continue to cycle through steps 1, 2, 3 and 4

explain:
Theoretically, a two-dimensional array should be created to represent the chessboard, but in fact, the problem can be solved by using a one-dimensional array through the algorithm. Arr [8] = {0, 4, 7, 5, 2, 6, 1, 3}. The corresponding arr subscript + 1 indicates the row, that is, the queen. For example, arr[i] = val, it indicates the i+1 Queen, which is placed in column val+1 of row i+1
code implementation
public class Queue8 {
//Define a max to indicate how many queens there are
int max = 8;
//Define the Array array and save the results of the Queen's placement position, such as arr = {0,4,7,5,2,6,1,3}
int[] array = new int[max];
//Cumulative number of problem solutions
static int count = 0;
//Number of conflicts
static int judgeCount = 0;
public static void main(String[] args) {
//Test 8 is correct
Queue8 queue8 = new Queue8();
queue8.check(0);
System.out.printf("Altogether%d solution", count);//92 species
System.out.printf("Total number of conflicts judged%d second", judgeCount); // 15720 times
}
//Write a method to place the n+1 Queen
//Special note: check means that for (int i = 0; I < max; I + +) will be entered into the check during each recursion, so there will be backtracking
private void check(int n) {
if(n == max) { //When n = 8, in fact, the eight queens have been placed
print();
return;
}
//Put the queen in turn and judge whether there is conflict
for(int i = 0; i < max; i++) {
//First, put the current queen n+1 in the first column of the row
array[n] = i;
//Judge whether there is a conflict when placing the n+1 Queen to column i
if(judge(n)) { // No conflict
//Then put the n+2 Queen, that is, start recursion
check(n+1); //
}
//If there is a conflict, continue to execute array[n] = i; That is, the nth queen is placed in a position where the line has to be moved back
}
}
//Check the method of detecting whether the n+1 Queen conflicts with the queen already placed in front after placing the n+1 Queen
/**
*
* @param n Represents the N + 1st queen
* @return
*/
private boolean judge(int n) {
judgeCount++;
for (int i = 0; i < n; i++) {
//explain
//1. array[i] == array[n] indicates whether the N + 1st queen is in the same column as the previous n queens
//2. Math.abs(n-i) == Math.abs(array[n] - array[i]) indicates whether the nth queen and the ith queen are in the same slash
// Put n = 1 to set column 2 1 n = 1 array[1] = 1
// Math.abs(1-0) == 1 Math.abs(array[n] - array[i]) = Math.abs(1-0) = 1
//3. It is not necessary to judge whether it is on the same line, because n is increasing every time
if (array[i] == array[n] || Math.abs(n-i) == Math.abs(array[n] - array[i])) {
return false;
}
}
return true;
}
//Method for outputting Queen's placement position
private void print() {
count++;
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + " ");
}
System.out.println();
}
}