1. Title
Title Link: P1169 "chessboard making" .
Title Description
Chess is one of the oldest game games in the world. It enjoys a high reputation with Chinese go, chess and Japanese general chess. It is said that chess originated from the thought of the book of changes. The chessboard is an 8 \times 8-size black-and-white square array, which corresponds to the eight eight hundred sixty-four trigrams, and black-and-white corresponds to Yin and Yang.
Our hero, little Q, is a chess enthusiast. As a top master, he was no longer satisfied with the ordinary chessboard and rules, so he and his good friend Xiao W decided to expand the chessboard to adapt to their new rules.
Xiao Q found a rectangular piece of paper composed of N \times M square squares, each of which was painted with one of black and white. Small Q wants to cut a part of this paper as a new chessboard. Of course, he wants this chessboard to be as large as possible.
However, Xiao Q has not decided whether to find a square chessboard or a rectangular chessboard (of course, no matter which kind, the chessboard must be black and white, that is, the adjacent grids are different colors), so he hopes to find the largest square chessboard area and the largest rectangular chessboard area, so as to decide which is better.
So little Q found you who will participate in the national informatics competition. Can you help him?
Input format
Contains two integers N and M, which represent the length and width of rectangular paper respectively. The next N rows contain a 01 matrix of N \ \times M, indicating the color of the rectangular piece of paper (0 indicates white and 1 indicates black).
Output format
Contains two lines, each containing an integer. The first line is the area of the largest square chessboard that can be found, and the second line is the area of the largest rectangular chessboard that can be found (note that squares and rectangles can intersect or contain).
Sample input and output
Enter #1
3 3 1 0 1 0 1 0 1 0 0
Output #1
4 6
Description / tips
For 20 \% data, N, M ≤ 80.
For 40 \% data, N, M ≤ 400.
For 100 \% data, N, M ≤ 2000.
2. Problem solving
analysis
Monotone stack (method 1)
At a glance, the online boss can see that the row number of black and white blocks in the chessboard is and is only one of the following two cases:
- The parity of the number of rows and columns where the black blocks are located is the same, but the white blocks are different.
- The parity of the row and column number of white blocks is the same, but the black blocks are different.
So we can scan the whole chessboard twice. For the first time, assuming that the chessboard meeting the requirements is the first case, then:
- Black and white blocks that meet the first condition are marked as 1.
- Black and white blocks that do not meet the first condition are marked as 0. Therefore, the maximum inner rectangle / square area of the chessboard that meets the requirements in the first case is the maximum inner rectangle / square area of the rectangle corresponding to the two-dimensional marker array. Convert to heel P4147 "jade toad Palace" Basically the same problem can be solved easily.
The second assumption is that the chessboard meeting the requirements is the second case, then:
- Black and white blocks that meet the second condition are marked as 1.
- Black and white blocks that do not meet the second condition are marked as 0. Therefore, the maximum inner rectangle / square area of the chessboard that meets the requirements in the second case is the maximum inner rectangle / square area of the rectangle corresponding to the two-dimensional marker array. Convert to heel P4147 "jade toad Palace" Basically the same problem can be solved easily.
The final answer is the maximum value of the maximum inner rectangle / square of the chessboard that meets one of the above two situations.
Monotone stack (method 2)
For konjaku, I don't have the insight of the big guys. My idea is this: similar P4147 "jade toad Palace" Similarly, scan the whole chessboard a[i][j],i \in [0,n), j \in [0,m) line by line, and record the maximum required column height b[i][j] corresponding to point (i,j), that is, the length of alternating black-and-white blocks from point (i,j):
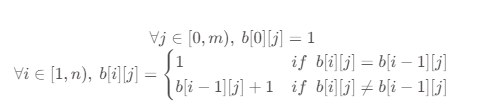
Then, the idea of monotone stack is also used to process each line separately. The difference is that when processing point (i,j):
- If a[i][j-1] \ne a[i][j], it means that for row I, column j meets the chessboard requirements formed at the end of column j-1. At this time, press b[i][j] according to the ordinary monotonic stack.
- If a[i][j-1] = a[i][j], it means that for row I, column j does not meet the requirements of the chessboard formed at the end of column j − 1. At this time, the chessboard has been split, that is, all columns after j cannot be combined with the columns in front of j to form a reasonable chessboard. Therefore, pop the stack empty, modify the rectangular boundary of the top of the stack to j − 1, and then press b[i][j] on the stack.
The whole idea is monotonous stack, but the stack pressing operation has been modified.
Hanging line method
This problem can also be solved by hanging line method. The hanging line method mainly involves three arrays:
- height[i][j]: used to indicate the highest height that can be reached by the point (i,j) upward.
- left[i][j]: used to represent the maximum left boundary that the point (i,j) can extend to the left.
- right[i][j]: used to represent the smallest right boundary that the point (i,j) can extend to the right.
The hanging line method first needs to initialize these three arrays:
\begin{array}{c} height[i][j] = 1 \\ left[i][j] = right[i][j] = 1 \end{array}
Then process each point by line, and the maximum left[i][j] and minimum right boundary that can be reached in the line:
\begin{array}{c} left[i][j] = left[i][j-1], \quad \text {if point} (i,j) \text {and point} (i,j-1) \text {there is no obstacle before point} \ \ right[i][j] = right[i][j+1], \quad \text {if point} (i,j) \text {and point} (i,j+1) \text {there is no obstacle between point} \ end{array}
Then, process the highest reachable height of the point (i,j) upward according to the column, and update the maximum left boundary and minimum right boundary of the maximum inner rectangle with this height at the same time:
\begin{array}{c} height[i][j] = h[i-1][j] + 1, \quad \text {if there is no obstacle between point} (i,j) \text {and point} (i-1,j) \text {\ \ left[i][j] = \max (left[i][j], left[i-1][j]) \ right[i][j] = \min (right[i][j], right[i-1][j]) \end{array}
Finally, calculate the maximum rectangular area that can be formed by points (i,j) upward (highest priority) left and right (second priority), and record the answers that meet the conditions.
code
Monotone stack (method 1)
#include <bits/stdc++.h>
#define MAXN 2005
using namespace std;
int ans1 = 0;
int ans2 = 0;
struct DC{
int i;
int v;
DC(): i(0),v(0) {}
DC(int _i, int _v): i(_i),v(_v) {}
};
void maxRectangle(int *b, int m) {
DC dc[MAXN];
int depth = 0;
dc[depth] = DC{-1,-1};
for(int j = 0; j < m; ++j) {
int sdepth = depth;
while(depth && b[j] <= dc[depth].v) {
int c = dc[sdepth].i - dc[depth-1].i;
int d = dc[depth].v;
ans1 = max(ans1, min(c*c, d*d));
ans2 = max(ans2, c*d);
--depth;
}
dc[++depth] = DC{j,b[j]};
}
int sdepth = depth;
while(depth) {
int c = dc[sdepth].i - dc[depth-1].i;
int d = dc[depth].v;
ans1 = max(ans1, min(c*c, d*d));
ans2 = max(ans2, c*d);
--depth;
}
}
int main()
{
int n, m;
static int a[MAXN][MAXN], b[MAXN][MAXN], c[MAXN][MAXN];
scanf("%d%d", &n, &m);
for(int i = 0; i < n; ++i) {
for(int j = 0; j < m; ++j) {
scanf("%d", &a[i][j]);
}
}
for(int i = 0; i < n; ++i) {
for(int j = 0; j < m; ++j) {
if((!((i&1)^(j&1)) && a[i][j]) || (((i&1)^(j&1)) && !a[i][j])){
b[i][j] = 1;
} else {
b[i][j] = 0;
}
}
}
for(int j = 0; j < m; ++j) {
c[0][j] = b[0][j];
}
for(int i = 1; i < n; ++i) {
for(int j = 0; j < m; ++j) {
if(b[i][j]) {
c[i][j] = c[i-1][j] + 1;
} else {
c[i][j] = 0;
}
}
}
for(int i = 0; i < n; ++i) {
maxRectangle(c[i], m);
}
for(int i = 0; i < n; ++i) {
for(int j = 0; j < m; ++j) {
if((!((i&1)^(j&1)) && a[i][j]) || (((i&1)^(j&1)) && !a[i][j])){
b[i][j] = 0;
} else {
b[i][j] = 1;
}
}
}
for(int j = 0; j < m; ++j) {
c[0][j] = b[0][j];
}
for(int i = 1; i < n; ++i) {
for(int j = 0; j < m; ++j) {
if(b[i][j]) {
c[i][j] = c[i-1][j] + 1;
} else {
c[i][j] = 0;
}
}
}
for(int i = 0; i < n; ++i) {
maxRectangle(c[i], m);
}
printf("%d\n%d\n", ans1, ans2);
return 0;
}Monotone stack (method 2)
#include <bits/stdc++.h>
#define MAXN 2005
using namespace std;
int ans1 = 0;
int ans2 = 0;
struct DC{
int i;
int v;
DC(): i(0),v(0) {}
DC(int _i, int _v): i(_i),v(_v) {}
};
void maxRectangle(int a[], int b[], int m) {
int depth = 0;
DC stack[MAXN];
stack[depth] = DC{-1,-1};
stack[++depth] = DC{0,b[0]};
for(int j = 1; j < m; ++j) {
int sdepth = depth;
if(a[j-1] != a[j]) {
while(depth && stack[depth].v >= b[j]) {
int c = stack[sdepth].i - stack[depth-1].i;
int d = stack[depth].v;
ans1 = max(ans1, min(c*c, d*d));
ans2 = max(ans2, c*d);
--depth;
}
} else {
while(depth) {
int c = stack[sdepth].i - stack[depth-1].i;
int d = stack[depth].v;
ans1 = max(ans1, min(c*c, d*d));
ans2 = max(ans2, c*d);
--depth;
}
stack[0].i = j - 1;
}
stack[++depth] = DC{j,b[j]};
}
int sdepth = depth;
while(depth) {
int c = stack[sdepth].i - stack[depth-1].i;
int d = stack[depth].v;
ans1 = max(ans1, min(c*c, d*d));
ans2 = max(ans2, c*d);
--depth;
}
}
int main()
{
int n, m;
static int a[MAXN][MAXN], b[MAXN][MAXN];
scanf("%d%d", &n, &m);
for(int i = 0; i < n; ++i) {
for(int j = 0; j < m; ++j) {
scanf("%d", &a[i][j]);
}
}
for(int j = 0; j < m; ++j) {
b[0][j] = 1;
}
for(int i = 1; i < n; ++i) {
for(int j = 0; j < m; ++j) {
if(a[i][j] != a[i-1][j]) {
b[i][j] = b[i-1][j] + 1;
} else {
b[i][j] = 1;
}
}
}
for(int i = 0; i < n; ++i) {
maxRectangle(a[i], b[i], m);
}
printf("%d\n%d\n", ans1, ans2);
return 0;
}Hanging line method
#include <bits/stdc++.h>
#define MAXN 2005
using namespace std;
int main()
{
int n, m;
static int a[MAXN][MAXN], l[MAXN][MAXN], r[MAXN][MAXN], h[MAXN][MAXN];
scanf("%d%d", &n, &m);
for(int i = 0; i < n; ++i) {
for(int j = 0; j < m; ++j) {
scanf("%d", &a[i][j]);
}
}
for(int i = 0; i < n; ++i) {
for(int j = 0; j < m; ++j) {
l[i][j] = j;
r[i][j] = j;
h[i][j] = 1;
}
}
// Process each line
for(int i = 0; i < n; ++i) {
for(int j = 1; j < m; ++j) {
if(a[i][j] != a[i][j-1]) {
l[i][j] = l[i][j-1];
}
}
for(int j = m-2; ~j; --j) {
if(a[i][j] != a[i][j+1]) {
r[i][j] = r[i][j+1];
}
}
}
// Process each column
for(int i = 1; i < n; ++i) {
for(int j = 0; j < m; ++j) {
if(a[i][j] != a[i-1][j]) {
h[i][j] = h[i-1][j] + 1;
l[i][j] = max(l[i][j], l[i-1][j]);
r[i][j] = min(r[i][j], r[i-1][j]);
}
}
}
int ans1 = 0;
int ans2 = 0;
for(int i = 0; i < n; ++i) {
for(int j = 0; j < m; ++j) {
int c = r[i][j] - l[i][j] + 1;
int d = h[i][j];
ans1 = max(ans1, min(c*c, d*d));
ans2 = max(ans2, c*d);
}
}
printf("%d\n%d\n", ans1, ans2);
return 0;
}