P2962 [USACO09NOV]Lights G
Luogu
Source: P2962 [USACO09NOV]Lights G
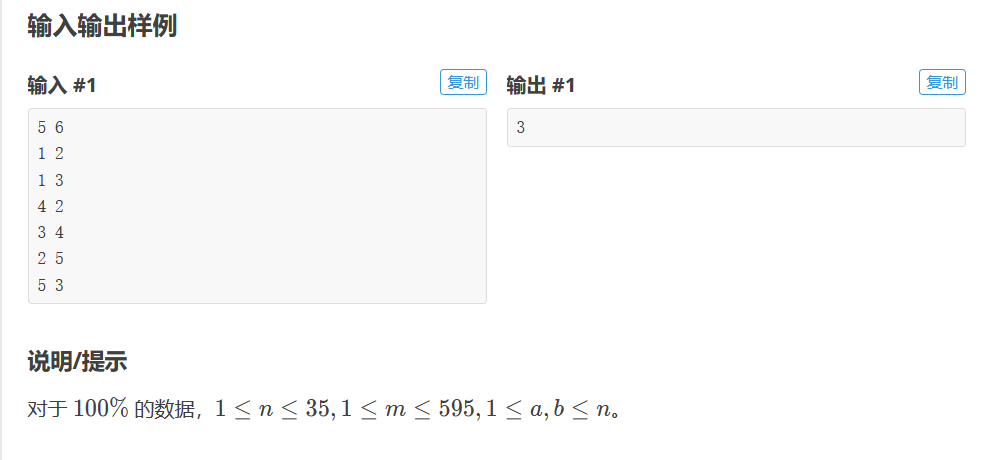
Meaning:
Given n points, the initial value is 0, m undirected edges, operate one point at a time, change itself and the point 1 connected to itself into 0, 0 into 1, and ask the minimum number of operations, so that all are 1
Idea:
I think the bosses are written by Gauss elimination + dfs, but I won't
Greedy: each point can be operated at most once
Violent search: first consider each state of violent search. The time complexity is 2^n, where n is up to 35. Obviously, it will timeout
Two way search: when we use two-way search, the time complexity will be reduced to about n*2^(n/2), which is a lot
The trick is to first define the f array to record the point that the ith point can reach. It can be realized by using the or operation. It can be detailed into a binary number. n is up to 35, so open long long
Put the results of the first half of the search into the hash, and find the hash in the second half of the search. If it happens to match, it is the answer
If you want to easily understand the following code, you can first understand binary and bit operations
#include <iostream>
#include <algorithm>
#include <map>
#include <unordered_map>
#include <cstring>
using namespace std;
typedef long long ll;
inline int read(void)//Read in
{
register int x = 0;
register short sgn = 1;
register char c = getchar();
while (c < 48 || 57 < c)
{
if (c == 45)
sgn = 0;
c = getchar();
}
while (47 < c && c < 58)
{
x = (x << 3) + (x << 1) + c - 48;
c = getchar();
}
return sgn ? x : -x;
}
inline void write(ll x)//output
{
if (x < 0)
putchar('-'), x = -x;
if (x > 9)
write(x / 10);
putchar(x % 10 + '0');
}
const int N = 40;
ll f[N];
unordered_map<ll, int> mp;
int main()
{
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
int n = read(), m = read();
int res = 0x7fffffff;//result
for (int i = 0; i < n; ++i)
f[i] = (1ll << i);//Each point can reach itself
for (int i = 1; i <= m; ++i)
{
int u = read(), v = read();
--u, --v;//Binary starts from one bit, subtracts one from each number, and then performs or operation. If you don't understand, you can draw it on the paper and understand it
f[u] |= (1ll << v);//u can reach v
f[v] |= (1ll << u);//v can reach the point u
}
for (int i = 0; i < (1 << (n >> 1)); ++i)//The core of two-way search is to search the state of the first half and operate on the first half
{
ll t = 0;//Record temporary status
int cnt = 0;//Record temporary results
for (int j = 0; j < (n >> 1); ++j)
{
if ((i >> j) & 1)//If j is selected
{
t ^= f[j];//Just XOR
++cnt;
}
}
if (!mp.count(t))//Last save hash table
mp[t] = cnt;
else
mp[t] = min(mp[t], cnt);
}
for (int i = 0; i < (1 << (n - (n >> 1))); ++i)//Second half state
{
ll t = 0;
int cnt = 0;
for (int j = 0; j < (n - (n >> 1)); ++j)
{
if ((i >> j) & 1)
{
t ^= f[(n >> 1) + j];//Since it starts from 0, but this search is the second half, all (n > > 1) + J represent our operations on the remaining points
++cnt;
}
}
if (mp.count(((1ll << n) - 1) ^ t))//If it can match exactly, update the minimum value
res = min(res, cnt + mp[((1ll << n) - 1) ^ t]);
}
write(res);//Output answer
return 0;
}
If you can't figure out what to do during the game, there are still ways. Refer to lo Gu Metaphysical algorithm of AuCloud
randomization
The first half is the same as the two-way search. An a array is added to record the serial number for random scrambling, once at a time, and then the sa() function traverses the operation points from front to back to determine whether the conditions are met
If it is satisfied, record the minimum value and exit. If it is not possible after traversal, return the maximum value and disrupt it again
This method is very metaphysical. It is A little similar to simulated annealing, but it does not have the essence of simulated annealing, but it is enough. It would be better if you can count A together and give points according to the test points in the competition
Look at the code comments
#include <iostream>
#include <algorithm>
#include <cstring>
#include <random>
#include <ctime>
using namespace std;
typedef long long ll;
inline int read(void)//Read in
{
register int x = 0;
register short sgn = 1;
register char c = getchar();
while (c < 48 || 57 < c)
{
if (c == 45)
sgn = 0;
c = getchar();
}
while (47 < c && c < 58)
{
x = (x << 3) + (x << 1) + c - 48;
c = getchar();
}
return sgn ? x : -x;
}
inline void write(ll x)//output
{
if (x < 0)
putchar('-'), x = -x;
if (x > 9)
write(x / 10);
putchar(x % 10 + '0');
}
const int N = 40;
ll f[N];
int a[N];
int n, m;
int sa()//Find the current result
{
ll ans = 0;
for (int i = 0; i < n; ++i)
{
ans ^= f[a[i]];
if (ans == (1ll << n) - 1)//If you can operate so that all points are 1
return i + 1;//i is from 0, all plus 1
}
return 0x7fffffff;
}
int main()
{
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
srand(time(NULL));//Random seed, it's up to him whether he can pass or not
n = read(), m = read();
int res = 0x7fffffff;
for (int i = 0; i < n; ++i)
{
a[i] = i;//Record number for random disruption
f[i] = (1ll << i);
}
for (int i = 1; i <= m; ++i)
{
int u = read(), v = read();
--u, --v;
f[u] |= (1ll << v);
f[v] |= (1ll << u);
}
int qaq;
if (n == 35)//Card time, no timeout
qaq = 1000000;
else
qaq = 1900000;
for (int i = 1; i <= qaq; ++i)
{
random_shuffle(a, a + n);//Random disorder order
int qwq = sa();//Judge whether the current situation meets the conditions
res = min(res, qwq);//Update minimum
}
write(res);
return 0;
}
Of course, you found that you didn't get 100, maybe more than 80 points, or more than 90 points. After all, metaphysics depends on your seeds. It's not recommended here. Don't use it unless you have to
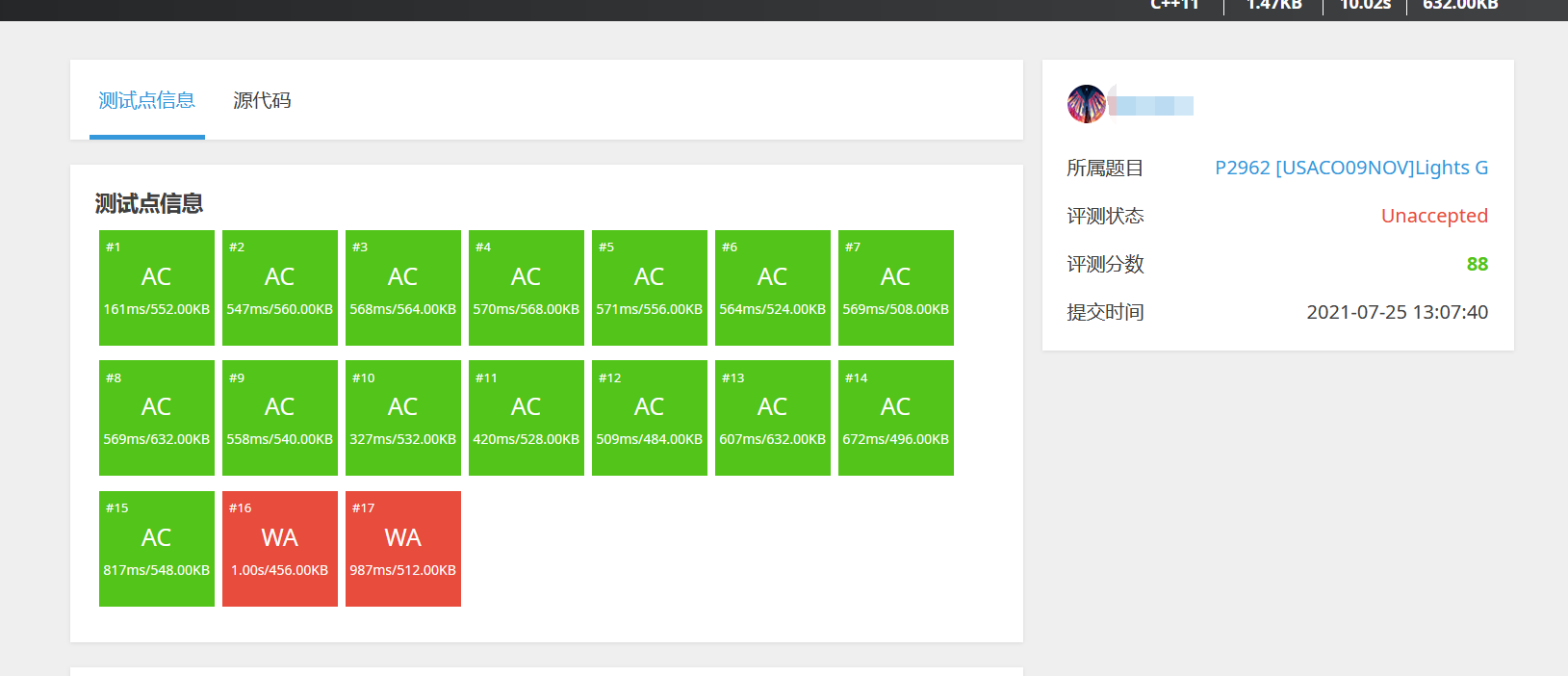I've tried it many times. I really don't recommend it. If it's a test point, it's still very good