introduction
In the Java collection, the importance of HashMap is self-evident. As a data structure for storing key value pairs, it has many application scenarios in daily development and is also a high-frequency test point in the interview. This article will analyze the put method in the HashMap collection.
HashMap underlying data structure
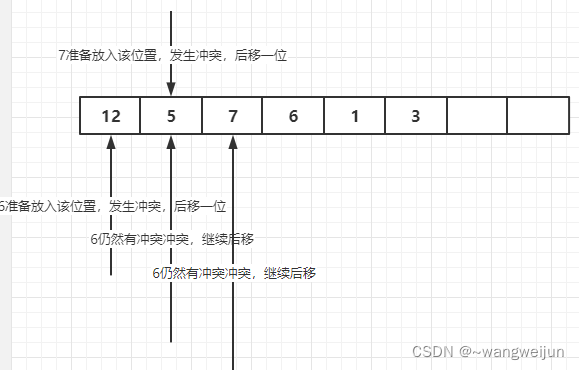
Let's first understand the underlying data structure of HashMap. It is essentially a hash table. In the data structure course, we should all have learned hash table. It is a data structure that can be accessed directly through key values, such as storing such a sequence: 5,12,7,6,1,3. First, we need to set a hash function through which we can locate the storage location of each element. For example, if the hash function is h (k) = k% 6, then the storage location of each element is: 1,0,1,0,1,3. At this time, the problem arises. After calculation, it is found that the storage locations of several elements are the same, but one location cannot store two values, which is a hash conflict. There are many ways to resolve hash conflicts:
- Linear detection method
- Pseudo random number method
- Chain address method
If a relatively simple linear detection method is adopted, the conflicting elements will be moved back one position. If there is still a conflict, continue to move back one bit, so as to obtain the storage position of each element:
In HashMap, of course, its design is much more sophisticated. Refer to its source code:
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
V value;
Node<K,V> next;
Node(int hash, K key, V value, Node<K,V> next) {
this.hash = hash;
this.key = key;
this.value = value;
this.next = next;
}
public final K getKey() { return key; }
public final V getValue() { return value; }
public final String toString() { return key + "=" + value; }
public final int hashCode() {
return Objects.hashCode(key) ^ Objects.hashCode(value);
}
public final V setValue(V newValue) {
V oldValue = value;
value = newValue;
return oldValue;
}
public final boolean equals(Object o) {
if (o == this)
return true;
if (o instanceof Map.Entry) {
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
if (Objects.equals(key, e.getKey()) &&
Objects.equals(value, e.getValue()))
return true;
}
return false;
}
}We found such a content class, which is a Node node. Therefore, we can guess that HashMap adopts the chain address method to solve the conflict. Where is the real storage location of HashMap data?
transient Node<K,V>[] table;
This is such a Node array.
Execution flow of put method
We directly understand the execution process of the put method in HashMap through a program. In the put method, HashMap needs to undergo initialization, value saving, capacity expansion, conflict resolution and other operations:
public static void main(String[] args) {
Map<String, String> map = new HashMap<>();
map.put("name", "zs");
map.put("age", "20");
map.put("name", "lisi");
map.forEach((k, v) -> {
System.out.println(k + "--" + v);
});
}We all know that the running result of this program is name--lisi age -- 20. Why is this result? The source code can tell us the answer.
First, execute the first line of code and call the parameterless construction method of HashMap:
public HashMap() {
this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}In the construction method, only a member variable of loadFactor is set, which represents the load factor of the hash table. The default value is 0.75. We will talk about what this load factor is later. Next, the program executes the put method:
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}The put method calls the putVal method and passes in the hash, key, value and other parameters of the key, so first calculate the hash of the key:
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}This hash is used to calculate the insertion position. We will later say that after calculating the hash of the key, it will call the putVal method:
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
Node<K,V> e; K k;
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}The first three lines of this method first define an array of Node type and a variable, and judge whether the table in the class member is empty. As we said earlier, this table is the real array to store data, and its initial value must be empty, so the resize method will be triggered:
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) {
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // double threshold
}
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
else { // zero initial threshold signifies using defaults
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
if (oldTab != null) {
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { // preserve order
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}The resize method is actually quite complex, but we pick out the important code. Because the initial value of table is null, it will enter the following branch:
else { // zero initial threshold signifies using defaults
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}It sets the values of two variables, newCap = 16, newThr = 0.75 * 16 = 12, where newCap is the capacity of the table array to be created this time, and newThr is the actual capacity that can only be stored.
For a hash table, if each position is filled with elements, a large number of conflicts must have occurred. However, if only a small part of the positions are used to store elements, the space of the hash table will be wasted. Therefore, after a lot of calculations, the predecessors come to the conclusion that the total capacity of the hash table * the value after 0.75 is the most appropriate storage capacity of the hash table, This 0.75 is called the load factor in the hash table. Therefore, when HashMap calls the put method for the first time, it will create a Node type array with a total capacity of 16 (provided that the parameterless construction method is called), but in fact, only 12 capacity can be used. When the 13th element is inserted, capacity expansion needs to be considered.
The next step is to initialize the table array:
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;By calling the resize method, we get an array of nodes with a capacity of 16, and then execute:
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);Remember this hash variable? It is the hash value of the key obtained earlier. By subtracting 1 from n (the length of the table array, i.e. 16) and performing an and operation with the hash value, the storage location of the data can be obtained. It is similar to the hash function H (k) = k% 6 mentioned at the beginning of the article. It also does this operation, hash% n. It should be noted that if the divisor is a power of 2 in the modulo operation, the modulo operation can be equivalent to the and operation of subtracting 1 from its divisor, that is, hash & (n - 1). Because the efficiency of the & operation is higher than that of the modulo operation, HashMap will design n as a power of 2.
After finding the position where the data needs to be inserted, you need to judge whether there are elements in the current position. Now there is no data in the table array, so the first judgment must be null. If the conditions are met, the execution code is: tab[i] = newNode(hash, key, value, null);, Create a node and store the hash value, key, value and their pointer fields:
Node<K,V> newNode(int hash, K key, V value, Node<K,V> next) {
return new Node<>(hash, key, value, next);
}Final execution:
++modCount;
if (++size > threshold)
resize();
afterNodeInsertion(evict);Judge whether the current capacity size exceeds the threshold. If it exceeds the threshold, you need to call the resize method to expand the capacity. Here, the first data name:zs is successfully inserted.
The second data age:20 is not analyzed here. It is the same as the name insertion process. Let's analyze the insertion of the third data name:lisi, which involves a key duplication problem. Let's see how HashMap handles it.
First, still call the putVal method, calculate the hash value of the key, and then judge whether the current table is empty. This time, the table must not be empty, so go directly to:
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);Still calculate the data insertion position through (n - 1) & hash. It is found that there is already an element at the position to be inserted, that is, name:zs. At this time, a conflict occurs. Execute:
Node<K,V> e; K k;
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;Now p is name:zs. By comparing the hash of p with the hash of the current data key, it is found that the hash value is the same. Continue to compare the key of p, that is, whether the name is the same as the key of the current data. If it is still the same, hand over p to e for management. Finally, execute:
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}At this time, e is not null, so set the value in e to the value of the current data. Therefore, HashMap successfully modifies the value with key name to lisi and returns the original value zs.
summary
To sum up, we can draw the following conclusions:
- The total capacity of HashMap must be the power of 2. Even if a capacity other than the power of 2 is passed in through the constructor, HashMap will expand it to the nearest power of 2; For example, if the total incoming capacity is 10, HashMap will automatically expand the capacity to 16
- If the parameterless construction method of HashMap is called, a Node array with a total capacity of 16 and an actual usable capacity of 12 will be initialized when the put method is executed for the first time
- When the actual capacity exceeds the threshold, HashMap will expand the capacity to twice the original capacity
- Implementation process of put method of HashMap: first, judge whether the current table is empty. If it is empty, initialize. If it is not empty, calculate the insertion position according to the hash of the key, and then judge whether there are elements in the position. If there are no elements, insert directly. If there are elements, judge whether the hash value of the original position data is the same as that of the data to be inserted. If they are the same, Continue to compare the values. If the values are different, create a new Node node and insert it behind the Node of the original data using the tail interpolation method to form a linked list. If the values are the same, overwrite the value of the original data with the value of the data to be inserted and return the value of the original data
- HashMap uses the chain address method to solve hash conflicts. Therefore, when the length of a linked list is greater than 8 and the length of the table array is greater than 64, the current linked list will be converted into a red black tree. If the length of the table array has not reached 64, the capacity will be expanded; When the length of the linked list is less than 6, the red black tree will be transferred back to the linked list
- Because HashMap will calculate the insertion position according to the hash value of the key, the hashCode method must be rewritten for the data type of the key, otherwise two identical keys will result in different hash values, and the equals method also needs to be rewritten, otherwise the equals method will compare the address value