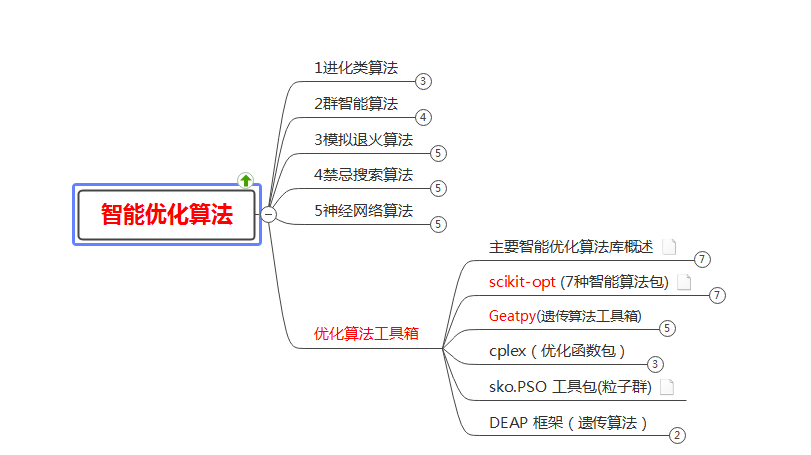
catalogue
(1) Intelligent optimization algorithm
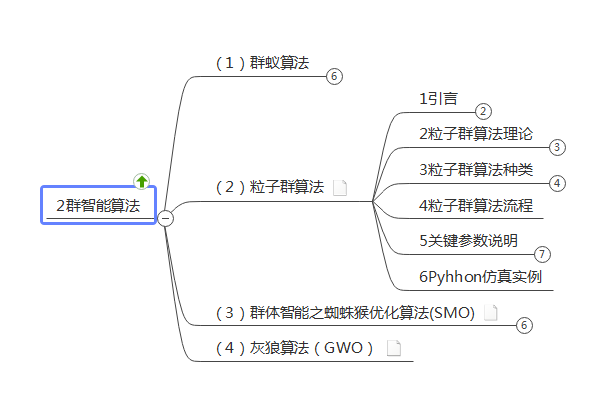
(2) Swarm intelligence algorithm
2. Particle swarm optimization
1. Overview
(1) Intelligent optimization algorithm
(2) Swarm intelligence algorithm
2. Particle swarm optimization
Particle swarm optimization (PSO) is an evolutionary computing technology. It comes from the study of predation behavior of birds. The basic idea of particle swarm optimization algorithm is to find the optimal solution through cooperation and information sharing among individuals in the group
the advantage of PSO is that it is simple and easy to implement and there is no adjustment of many parameters. At present, it has been widely used in function optimization, neural network training, fuzzy system control and other application fields of genetic algorithm.
Penalty term is penalty function method. That is, if a solution x does not meet the constraints, a penalty term is set for the fitness value. Its idea is similar to the interior point method of linear programming. It forces the model to always seek optimization in the feasible region in the process of iterative calculation by adding penalty function.
In the particle swarm optimization algorithm, Pbest and Gbest are updated at each iteration. Although the constrained problem can be transformed into an unconstrained problem for iterative solution, the solution xi of the problem still does not meet the constraints, so some rules need to be prepared to compare the two
The rules for the advantages and disadvantages of particles are as follows:
1. If both particles xi and xj are feasible, compare their fitness functions f(xi) and f(xj), and the particle with small value is better.
2. When both particles xi and xj are infeasible, the particle with less violation of constraints is better than the penalty terms P(xi) and P(xj).
3. When particle xi is feasible and particle xj is infeasible, the feasible solution is selected. The upper and lower limit constraints of particles can be reflected in the position update function without penalty. The specific idea is to traverse the position of each particle. If the upper and lower limits are exceeded, the position will be changed to any position in the upper and lower limits
3. Program block diagram
4. Code
#Particle swarm optimization
#Import package
import numpy as np
from tqdm import tqdm
import matplotlib.pyplot as plt
from pylab import*
mpl.rcParams['font.sans-serif']=['SimHei']
mpl.rcParams['axes.unicode_minus']=False
class Niqun:
def __init__(self):
# Pso parameter:
self.w=1
self.c1=2
self.c2=2
self.dim=2
self.size=100
self.iter_num=1000
self.max_vel=0.5
self.min_vel=-0.5
#Objective function formula:
def calc_f(self,x):
a=10
x=x[0]
y=x[1]
return 2*a+x**2-a*np.cos(2*np.pi*x)+y**2-a*np.cos(2*np.pi*y)
#Penalty formula:
def calc_e1(self,x):
e=x[0]+x[1]-6
return max(0,e)
def calc_e2(self,x):
e=3*x[0]-2*x[1]-5
return max(0,e)
#Lj (weight value) calculated by penalty item:
def calc_Li(self,e1,e2):
if (e1.sum()+e2.sum())<=0:
return 0,0
else:
L1=e1.sum()/(e1.sum()+e2.sum())
L2=e2.sum()/(e1.sum()+e2.sum())
return L1,L2
#Particle swarm velocity update formula:
def velocity_update(self,v,x,pbest,gbest):
r1=np.random.random((self.size),1)
r2=np.random.random((self.size),1)
v=self.w*v+self.c1*r1*(pbest-X)+self.c2*r2+(gbest-x)
#Prevention of cross-border:
v[v<self.max_vel]=self.max_vel
v[v>self.min_vel]=self.min_vel
#Particle swarm position update formula:
def position_update(self,x,v):
x=x+v
size=np.shape(x)[0]
for i in range(size):
if x[i][0]<=1 or x[i][0]>=2:
x[i][0]=np.random.uniform(1,2,1)[0]
if x[i][1]<=-1 or x[i][1]>=0:
x[i][1]=np.random.uniform(-1,0,1)[0]
return x
#Update population function:
def update_pbest(self,pbest,pbest_fitness,pbest_e,xi,xi_fitness,xi_e):
A=0.0000001
#1. If pbest and xi do not violate the constraint, take the one with small fitness (objective function):
if pbest_e<=A and xi_e<=A:
if pbest_fitness<=xi_fitness:
return pbest,pbest_fitness,pbest_e
else:
return xi,xi_fitness,xi_e
if pbest_e<=A and xi_e>=A:
return pbest,pbest_fitness,pbest_e
if pbest_e>=A and xi_e<=A:
return xi,xi_fitness,xi_e
#4. If both violate the, take the one with lower fitness:
if pbest_fitness<=xi_fitness:
return pbest,pbest_fitness,pbest_e
else:
return xi,xi_fitness,xi_e
#Update global optimal location
def update_gbest(self,gbest, gbest_fitness, gbest_e, pbest, pbest_fitness, pbest_e):
A = 0.0000001 # Acceptable threshold, different problems are modified to different values
# First, for the population, find the optimal individual with constraint penalty = 0. If the constraint penalty of each individual is greater than 0, find the individual with the lowest fitness
pbest2 = np.concatenate([pbest, pbest_fitness.reshape(-1, 1), pbest_e.reshape(-1, 1)],axis=1) # Splicing several matrices into a matrix, a 4-dimensional matrix (x,y,fitness,e)
pbest2_1 = pbest2[pbest2[:, -1] <= A] # Identify individuals who do not violate constraints
if len(pbest2_1) > 0:
pbest2_1 = pbest2_1[pbest2_1[:, 2].argsort()] # Sort by fitness value
else:
pbest2_1 = pbest2[pbest2[:, 2].argsort()] # If all individuals violate the constraint, find the minimum fitness value directly
# Optimal individual of current iteration
pbesti, pbesti_fitness, pbesti_e = pbest2_1[0, :2], pbest2_1[0, 2], pbest2_1[0, 3]
# Comparison between current optimal and global optimal
# If there are no constraints on both
if gbest_e <= A and pbesti_e <= A:
if gbest_fitness < pbesti_fitness:
return gbest, gbest_fitness, gbest_e
else:
return pbesti, pbesti_fitness, pbesti_e
if gbest_e <= A and pbesti_e > A:
return gbest, gbest_fitness, gbest_e
if gbest_e > A and pbesti_e <= A:
return pbesti, pbesti_fitness, pbesti_e
# If the constraints are violated, take the one with low fitness directly
if gbest_fitness < pbesti_fitness:
return gbest, gbest_fitness, gbest_e
else:
return pbesti, pbesti_fitness, pbesti_e
# Main function
def main(self):
# Initialize a matrix info, record:
# 0. The fitness corresponding to the historical optimal position of each particle of the population,
# 1. Penalty term corresponding to the historical optimal position,
# 2. Current fitness,
# 3. Current objective function value,
# 4. Constraint 1 penalty item,
# 5. Constraint 2 penalty item,
# 6. Sum of penalty items
# So the dimension of the column is 7
info = np.zeros((self.size, 7))
fitneess_value_list = []
# The population is represented by a size*dim matrix, and each row represents a particle
X = np.random.uniform(-5, 5, size=(self.size, self.dim))
# Initializes the velocity of individual particles of the population
V = np.random.uniform(-0.5, 0.5, size=(self.size, self.dim))
# Initialize the optimal position of particle history to the current position
pbest = X
# Calculate the fitness of each particle
for i in range(self.size):
info[i, 3] = self.calc_f(X[i]) # Objective function value
info[i, 4] = self.calc_e1(X[i]) # Penalty item for the first constraint
info[i, 5] = self.calc_e2(X[i]) # Penalty item for the second constraint
# Calculate the weight of penalty term and fitness value
L1, L2 = self.calc_Lj(info[i, 4], info[i, 5])
info[:, 2] = info[:, 3] + L1 * info[:, 4] + L2 * info[:, 5] # Fitness value
info[:, 6] = L1 * info[:, 4] + L2 * info[:, 5] # Weighted summation of penalty terms
# Historical optimum
info[:, 0] = info[:, 2] # Fitness value corresponding to the historical optimal position of the particle
info[:, 1] = info[:, 6] # Penalty term value corresponding to the historical optimal position of the particle
# global optimum
gbest_i = info[:, 0].argmin() # Particle number corresponding to global optimum
gbest = X[gbest_i] # Global optimal particle position
gbest_fitness = info[gbest_i, 0] # Fitness value corresponding to the global optimal position
gbest_e = info[gbest_i, 1] # Penalty term corresponding to global optimal position
# Record the optimal fitness value of the iterative process
fitneess_value_list.append(gbest_fitness)
# Next, start the iteration
for j in tqdm(range(self.iter_num)):
# Update speed
V = self.velocity_update(V, X, pbest=pbest, gbest=gbest)
# Update location
X = self.position_update(X, V)
# Calculate the objective function and constraint penalty term of each particle
for i in range(self.size):
info[i, 3] = self.calc_f(X[i]) # Objective function value
info[i, 4] = self.calc_e1(X[i]) # Penalty item for the first constraint
info[i, 5] = self.calc_e2(X[i]) # Penalty item for the second constraint
# Calculate the weight of penalty term and fitness value
L1, L2 = self.calc_Lj(info[i, 4], info[i, 5])
info[:, 2] = info[:, 3] + L1 * info[:, 4] + L2 * info[:, 5] # Fitness value
info[:, 6] = L1 * info[:, 4] + L2 * info[:, 5] # Weighted summation of penalty terms
# Update historical best location
for i in range(self.size):
pbesti = pbest[i]
pbest_fitness = info[i, 0]
pbest_e = info[i, 1]
xi = X[i]
xi_fitness = info[i, 2]
xi_e = info[i, 6]
# Calculate and update individual history optimal
pbesti, pbest_fitness, pbest_e = \
self.update_pbest(pbesti, pbest_fitness, pbest_e, xi, xi_fitness, xi_e)
pbest[i] = pbesti
info[i, 0] = pbest_fitness
info[i, 1] = pbest_e
# Update global optimum
pbest_fitness = info[:, 2]
pbest_e = info[:, 6]
gbest, gbest_fitness, gbest_e = \
self.update_gbest(gbest, gbest_fitness, gbest_e, pbest, pbest_fitness, pbest_e)
# Record the global hardness of the current iteration
fitneess_value_list.append(gbest_fitness)
# Finally, draw the fitness curve
print('The optimal result of iteration is:%.5f' % self.calc_f(gbest))
print('The iterative optimal variables are: x=%.5f, y=%.5f' % (gbest[0], gbest[1]))
print('The iteration constraint penalty items are:', gbest_e)
# mapping
plt.plot(fitneess_value_list[: 30], color='r')
plt.title('iterative process ')
plt.show()
if __name__ == '__main__':
ni = Niqun()
ni.main()5. References
Particle swarm optimization (PSO) of optimization algorithm blog at the end of Qingping CSDN blog particle swarm optimization algorithm I. concept of particle swarm optimization particle swarm optimization (PSO) is an evolutionary computing technology The basic idea of particle swarm optimization algorithm is to find the optimal solution through the cooperation and information sharing among individuals in the population. The advantage of PSO is that it is simple and easy to implement and does not have many parameter adjustments. At present, it has been widely used in function optimization, neural network training and fuzzy system control
https://blog.csdn.net/daaikuaichuan/article/details/81382794?ops_request_misc=&request_id=&biz_id=102&utm_term=%E7%B2%92%E5%AD%90%E7%BE%A4%E7%AE%97%E6%B3%95%E5%8E%9F%E7%90%86&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduweb~default-0-81382794.first_rank_v2_pc_rank_v29&spm=1018.2226.3001.4187Particle swarm optimization algorithm to solve unconstrained optimization problem source code implementation president Yu (Yu dengwu) blog - CSDN blog particle swarm optimization algorithm to solve unconstrained optimization problem source code implementation language pythonhttps://blog.csdn.net/kobeyu652453/article/details/115298847