Catalog
1. Title Description

Sample Input 1:
10 3 1 2 8 7 5 9 4 6 0 1 2 3 7 8 5 9 4 6 0
Sample Output 1:
Insertion Sort 1 2 3 5 7 8 9 4 6 0
Sample Input 2:
10 3 1 2 8 7 5 9 4 6 0 6 4 5 1 0 3 2 7 8 9
Sample Output 2:
Heap Sort 5 4 3 1 0 2 6 7 8 9
The main idea of the topic
The original sequence and partially sorted sequence are given to determine whether to insert or heap sort. (similar to this question *PAT a (c + +) [insert sort / merge sort])
supplement
Heap sort @Dreamcatcher CX
Heap sort
You can use an array to simulate a large root heap (when sorting in ascending order, use a large root heap with the maximum value at the end each time). When the root node is i, the left and right children are 2*i+1 and 2*i+2 respectively;
- Design down filter function;
- Use this function to build a large root heap;
- After the large root heap is built, each time the root is exchanged with the end of the unsorted part of the array (after the exchange, this element is sorted), and the large root heap structure of the unsorted part is readjusted. One maximum value can be adjusted to the end of the array at a time;
2, train of thought
Refer to Liu Shen's code.
According to the characteristics of sorting, judge:
Insert sort:
- In the tar array, the first p elements are ordered (from small to large), and the later elements are the same as the initial array init;
- If the condition 1 is met, it is considered as insertion sort, just sort tar further: sort(tar, tar + index + 1);
Heap sort:
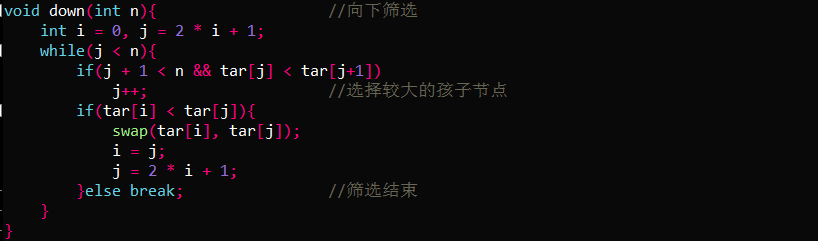
- Principle: when sorting by increasing order, set the sequence to large root heap. Exchange the root node of the big root heap with the last element of the unsorted part of the array every time, and then readjust the structure of the tree (array form): from top to bottom, compare with the older children in the left and right children, if it is smaller than the older children, exchange with it, then take the child node as the root, and continue to adjust downward; if it is larger than the older children, the adjustment is terminated. The adjustment function down is as follows (subscript starts from 0, left child 2*i+1, right child 2*i+2):
- After the insertion sort is negated, it can be determined as heap sort. Traversal from back to front
 , find the position p of the first element less than tar[0];
, find the position p of the first element less than tar[0]; - To do the next heap sort, first:
 ;
; - Readjust the structure of the large top reactor
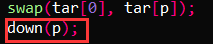 ;
;
3, AC code
#include<bits/stdc++.h>
using namespace std;
int init[101], tar[101], N; //init initial array tar partial sort array
void down(int n){ //Downward selection
int i = 0, j = 2 * i + 1;
while(j < n){
if(j + 1 < n && tar[j] < tar[j+1])
j++; //Select the older child node
if(tar[i] < tar[j]){
swap(tar[i], tar[j]);
i = j;
j = 2 * i + 1;
}else break; //End of screening
}
}
int main(){
#ifdef ONLINE_JUDGE
#else
freopen("1.txt", "r", stdin);
#endif // ONLINE_JUDGE
scanf("%d", &N);
for(int i = 0; i < N; i++)
scanf("%d", &init[i]);
for(int i = 0; i < N; i++)
scanf("%d", &tar[i]);
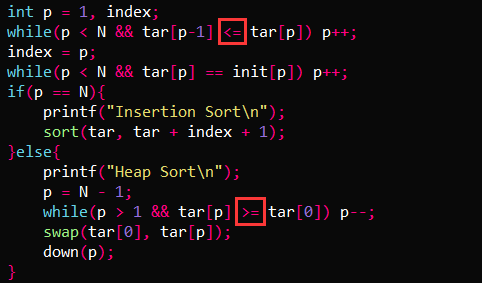
int p = 1, index;
while(p < N && tar[p-1] <= tar[p]) p++;
index = p;
while(p < N && tar[p] == init[p]) p++;
if(p == N){
printf("Insertion Sort\n");
sort(tar, tar + index + 1);
}else{
printf("Heap Sort\n");
p = N - 1;
while(p > 1 && tar[p] >= tar[0]) p--;
swap(tar[0], tar[p]);
down(p);
}
printf("%d", tar[0]);
for(int i = 1; i < N; i++)
printf(" %d", tar[i]);
return 0;
}
4. Problem solving process
First stroke
Determine which sort is based on the rule, and make another sort based on tar:
#include<bits/stdc++.h>
using namespace std;
int init[101], tar[101], N;//init initial array tar partial sort array
void down(int n){
int i = 0, j = 2 * i + 1;
while(j < n){
if(j + 1 < n && tar[j] < tar[j+1])
j++;//Choose older children
if(tar[i] < tar[j]){
swap(tar[i], tar[j]);
i = j;
j = 2 * i + 1;
}else break;
}
}
int main(){
#ifdef ONLINE_JUDGE
#else
freopen("1.txt", "r", stdin);
#endif // ONLINE_JUDGE
scanf("%d", &N);
for(int i = 0; i < N; i++)
scanf("%d", &init[i]);
for(int i = 0; i < N; i++)
scanf("%d", &tar[i]);
int p = 1, index;
while(tar[p-1] < tar[p]) p++;
index = p;
while(p < N && tar[p] == init[p]) p++;
if(p == N){
printf("Insertion Sort\n");
sort(tar, tar + index + 1);
}else{
printf("Heap Sort\n");
p = N - 1;
while(tar[p] > tar[0]) p--;
swap(tar[0], tar[p]);
down(p);
}
printf("%d", tar[0]);
for(int i = 1; i < N; i++)
printf(" %d", tar[i]);
return 0;
}
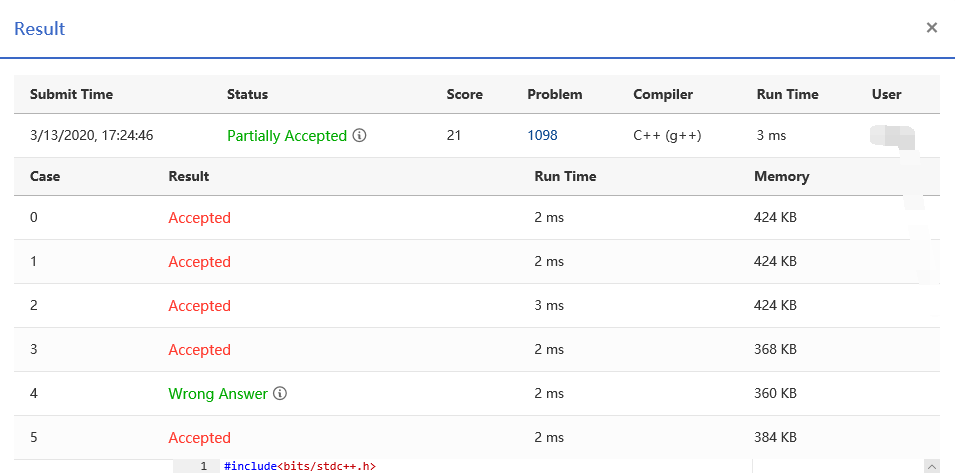
Second stroke
Note that the title does not say that each number in the sequence is unique. Therefore, the = sign is added to the judgment condition