Octree octree
Octree (octree) structure is a data model first proposed by Dr. Hunter in 1978. Octree structure divides the geometric entities in three-dimensional space by volume elements, and each volume element has the same time and space complexity. The geometric objects in three-dimensional space are divided by cyclic recursive division method, so as to form a directional graph with root nodes In the structure, if the divided voxel has the same attributes, the voxel constitutes a leaf node; Otherwise, continue to divide the voxel into 8 sub cubes and divide them successively, as shown in the following schematic diagram.
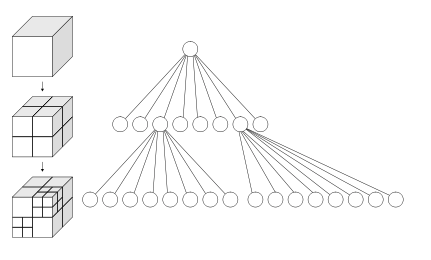
Octree is a tree data structure used to describe three-dimensional space. Each node of the octree represents a cube volume element, and each node has eight leaf nodes. The volume elements represented by these eight leaf nodes together are equal to the volume of the parent node. The general center point is used as the sub center of the node. If the octree is not an empty tree, there will only be eight or zero child nodes of any node in the tree, and there will be no number of child nodes other than 0 and 8.
The resolution of octree refers to the size of the lowest leaf node. If the resolution is set to 0.01m, each leaf node is a small square of 1cm.
In short, the storage structure of octree can be used to find the corresponding elements, divide the cube in turn, find the small cube corresponding to the search elements, and then divide and search again.
The nodes of the generated octree can be divided into three categories:
- Gray node: the of the corresponding cube is occupied by the search element;
- White node: the corresponding cube does not find the content of the element;
- Black node: its corresponding cubes are all occupied by lookup elements.
Reference link: Octree learning
2 nearest neighbor search within radius
Neighbors within Radius Search refers to a point in the search point cloud ball body half path R Sphere radius R All nearest neighbors within sphere radius R.
3 code implementation
Description: search for the 100th point in the point cloud within the sphere radius R = 0.2 m R=0.2m R = nearest neighbor within 0.2m.
code:
#define BOOST_TYPEOF_EMULATION
#include <pcl/io/pcd_io.h>
#include <pcl/octree/octree.h>
#include <pcl/console/time. h> // For timing
using namespace std;
typedef pcl::PointXYZ PointT;
typedef pcl::PointCloud<PointT> PointCloudT;
int main()
{
//--------------------------Load point cloud--------------------------
cout << "->Loading point cloud..." << endl;
PointCloudT::Ptr cloud(new PointCloudT);
if (pcl::io::loadPCDFile("1.pcd", *cloud) < 0)
{
PCL_ERROR("\a->Point cloud file does not exist!\n");
system("pause");
return -1;
}
cout << "->Load point cloud points:" << cloud->points.size() << endl;
//==========================Load point cloud==========================
pcl::console::TicToc time;
time.tic(); //Start timing
//-------------------------Building Octree-------------------------
float resolution = 0.2; //Resolution, that is, the size of the lowest leaf node
pcl::octree::OctreePointCloudSearch<PointT> octree(resolution); //Initialize octree
octree.setInputCloud(cloud); //Set input point cloud
octree.addPointsFromInputCloud(); //Building octree
//=========================Building Octree=========================
//------------------------Within radius nearest neighbor search-----------------------
PointCloudT cloud_r_neighbors; //Nearest neighbor within storage radius
PointT searchPoint = cloud->points[100]; //Set search point
float radius = 0.2; //Neighborhood radius
std::vector<int>pointIdxRadiusSearch; //Index for storing R nearest neighbors
std::vector<float>pointRadiusSquaredDistance; //Square distance of nearest neighbor
if (octree.radiusSearch(searchPoint, radius, pointIdxRadiusSearch, pointRadiusSquaredDistance) > 0)
{
cout << "->Search point coordinates:" << searchPoint << endl;
cout << "->R Number of nearest neighbors:" << pointIdxRadiusSearch.size() << endl;
cout << "->R Nearest neighbor coordinates and square distance:" << endl;
for (size_t i = 0; i < pointIdxRadiusSearch.size(); ++i)
{
//Cout < < cloud - > points [pointidxradiussearch [i]] < "square distance:" < pointradiussquareddistance [i] < < endl;
cloud_r_neighbors.push_back(cloud->points[pointIdxRadiusSearch[i]]);
}
cout << "->Time consuming:" << time.toc() / 1000 << " s" << endl;
//Save R nearest neighbor
pcl::io::savePCDFileBinary("cloud_r_neighbors.pcd", cloud_r_neighbors);
cout << "->R Nearest neighbor details:\n" << cloud_r_neighbors << endl;
}
//========================Within radius nearest neighbor search=======================
return 0;
}
Output results:
->Loading point cloud... ->Number of point clouds loaded: 41049 ->Search point coordinates:(-0.015396,-0.29139,-1.901) ->R Number of nearest neighbors: 1000 ->R Nearest neighbor coordinates and square distance: ->Time consuming: 0.125 s ->R Nearest neighbor details: points[]: 1000 width: 1000 height: 1 is_dense: 1 sensor origin (xyz): [0, 0, 0] / orientation (xyzw): [0, 0, 0, 1]
Comparison of time consumption of different resolutions (average value of multiple experiments)
| resolving power | 2m | 0.2m | 0.02m |
|---|---|---|---|
| time consuming | 0.168 s | 0.125 s | 0.233 s |
According to the experimental results, it can be preliminarily concluded that the higher the resolution of octree, the faster the search speed is not necessarily.
Due to the small number of experimental point clouds, interested partners can explore by themselves.
Therefore, it is recommended to avoid setting the resolution KD tree for nearest neighbor search within radius R
4 result display

The white point is the original point cloud
The red point is the neighborhood point within the radius corresponding to the 100th point in the original point cloud, R = 0.2 m R=0.2m R=0.2m
5 attention
- Neighborhood points are sorted from small to large according to the square distance from the search point. The point with the smallest distance is the search point itself (if the search point is a point in the original point cloud).
- When the search point s e a r c h P o i n t searchPoint When searchPoint is a point in the original point cloud, the nearest neighbor within its radius includes the search point itself; Otherwise, not included.
Related links: