Perfect Square for the Sixth Blue Bridge Cup 2015

Title:

Title: Perfect Square

If some squares with different sides and lengths fit exactly into a larger square, they are called perfect squares.

Historically, it took a long time for people to find some perfect squares.For example: 22 squares as long as
2 3 4 6 7 8 12 13 14 15 16 17 18 21 22 23 24 26 27 28 50 60
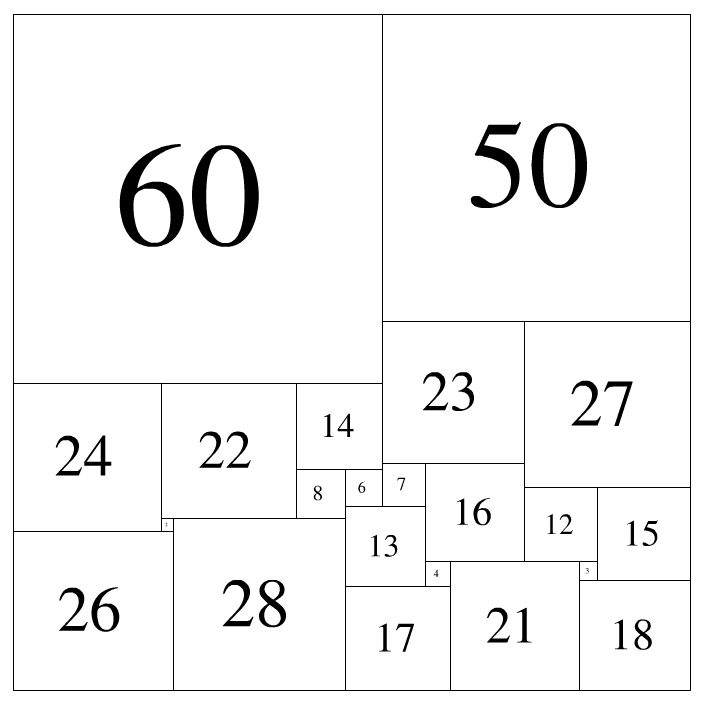
Combining them like [Figure 1.png] is a solution.At this point,
Closely to the top edge is: 6050
Closely to the bottom edge is: 26 28 17 21 18

There are 8 types of 22-order perfect squares.The following combination is another:
2 5 9 11 16 17 19 21 22 24 26 30 31 33 35 36 41 46 47 50 52 61
If you tell you that the scheme is close to the top edge, the order from left to right is: 47 46 61,
Can you figure out which squares are next to the bottom edge?

Submit the length of the square next to the bottom edge, left to right, separated by spaces.

Do not fill in any redundant content or captions.

Questions:

Express deep disdain ->-> (envy, jealousy, hate) for someone who handpaints perfect squares in an examination ground

dfs

Divide the whole large square into 154*154 cells. Search for an unfilled grid from top to bottom and left to right for each search, select an unplaced legal placement, and fill the corresponding position with 1.When all 19 small squares are placed, they exit recursively.

public class PerfectSquare {
    static int[] a = new int[] { 2, 5, 9, 11, 16, 17, 19, 21, 22, 24, 26, 30, 31, 33, 35, 36, 41, 50, 52 };
    static int[] vis = new int[19], ans = new int[19];
    static int []last=new int[100],lx=new int[4],ly=new int[4] ;//Store the length, x-coordinates, and p-coordinates of the last row
    static int len = 154,next=0;//Index of last row
    static int[][] matvis = new int[len][len];
    static int[][] mat = new int[154][154];

    static void mark(int bx, int by, int len) {
        for (int i = bx; i < bx + len; i++)
            for (int j = by; j < by + len; j++)
                mat[i][j] = 1;

    }

    static void unmark(int bx, int by, int len) {
        for (int i = bx; i < bx + len; i++)
            for (int j = by; j < by + len; j++)
                mat[i][j] = 0;

    }

    static boolean pd(int bx, int by, int len) {

        for (int i = bx; i < bx + len; i++)
            for (int j = by; j < by + len; j++) {
                if(i>=154||j>=154){
                    return false;
                }

                if (mat[i][j] == 1)
                    return false;
            }

        return true;
    }

    static void dfs(int ind) {

        if (ind == 19) {
            for (int i = 0; i < 19; i++)
                System.out.print(ans[i] + ",");
            System.out.println(next);

            for(int i=0;i<next;i++){
                System.out.println(lx[i]+","+ly[i]+","+last[i]);
            }
            return;
        }
        int bx = 0, by = 0;
        boolean flag=false;
        for (int i = 0; i < len; i++){


            for (int j = 0; j < len; j++) {
                if (mat[i][j] == 0) {
                    bx = i;
                    by = j;
                    flag=true;
                    break;
                }

            }
            if(flag) break;
        }
      // System.out.println("ind:"+ind+"begin:"+bx+","+by);
        for (int i = 0; i < 19; i++) {
            if (vis[i] == 0 && pd(bx, by, a[i])) {
        //      System.out.println("ind:"+ind+","+a[i]);
                vis[i] = 1;
                ans[ind] = a[i];
                if(bx+a[i]==154){
                    //System.out.println("lastline");
                    //System.out.println(next);
                    last[next]=a[i];
                    lx[next]=bx;
                    ly[next]=by;
                    next++;
                }
                mark(bx, by, a[i]);

                dfs(ind + 1);
                vis[i] = 0;
                unmark(bx, by, a[i]);
                if(bx+a[i]==154){

                    next--;
                }
            }

        }
    }

    public static void main(String[] args) {
        mark(0,0,47);
        mark(0,47,46);
        mark(0,93,61);

        /*for (int i = 0; i < len; i++){
            for (int j = 0; j < len; j++) {
                System.out.print(mat[i][j]);
            }
            System.out.println();
        }*/

          dfs(0);
    }
}

Print results:

22,24,26,21,9,52,5,36,2,35,31,50,17,16,19,11,41,33,30,4
104,0,50
113,113,41
121,50,33
124,83,30

Behavior 1 search results, Behavior 2-5 follows the upper left coordinates and edge lengths of several squares along the lower edge, and from left to right four ordinate coordinates from small to large. The answer is:
50 33 30 41