Persistent data structure
1. Principle of persistent data structure
principle
- Persistence: record all historical versions of the data structure, which is called persistence.
- Not all data structures can be persistent. Persistent data structures require stable structure, such as heap (a full binary tree with stable structure), tree array, trie (dictionary tree), line segment tree, etc. The balance tree cannot be persisted because it has left-handed and right-handed operations.
- There are two ways to save all historical versions. One is to back up all the versions after each change; The other is incremental backup. The first method has high space-time complexity. Instead of using this method, we will only explain the incremental backup method (similar to git).
- The core idea of incremental backup is to record only the parts of each version that are different from the previous version.
- Here we explain the persistence of trie and the persistence of segment tree (also known as chairman tree).
Persistence of trie
- For trie, we only record different parts each time, which saves more space.
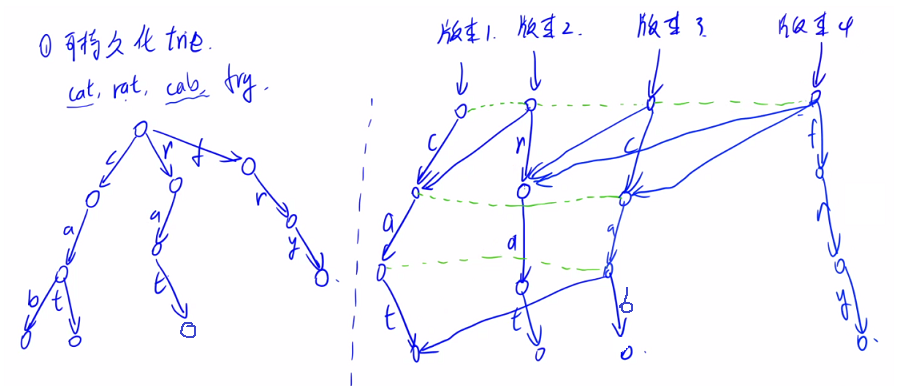
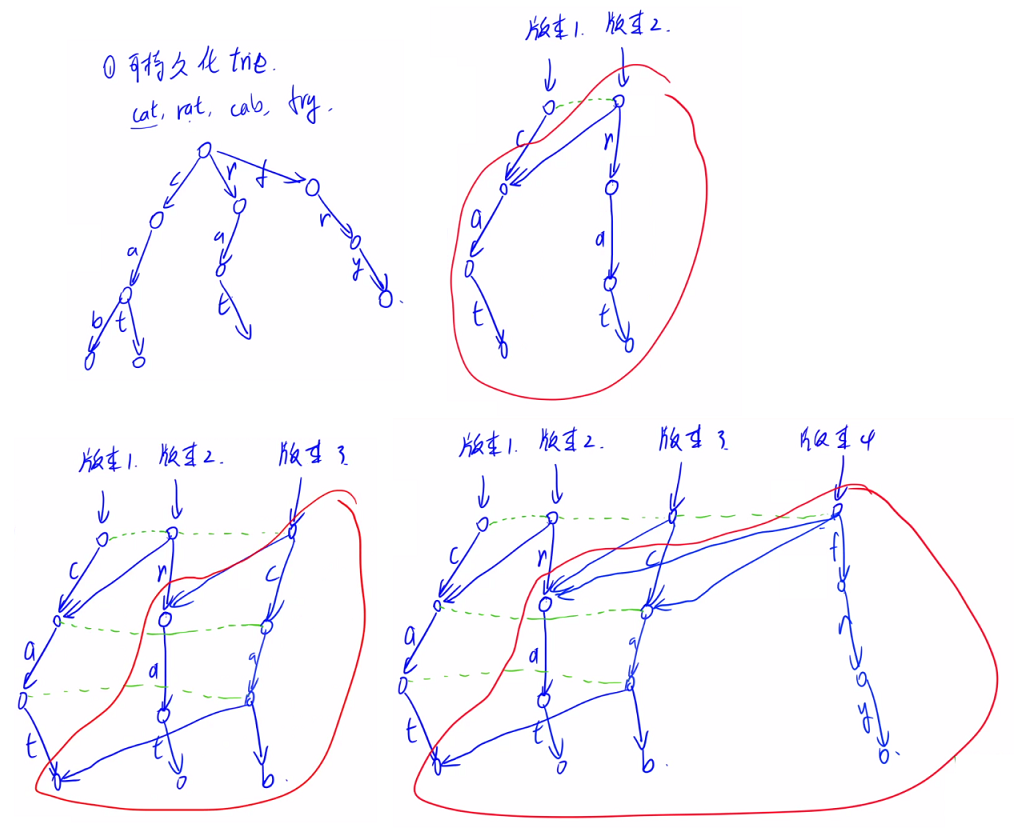
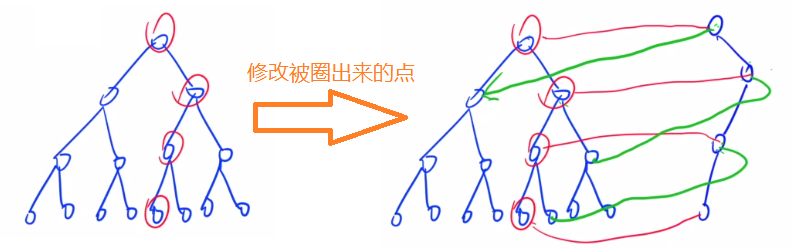
- All changed nodes must be split, because the following nodes will change every time. Therefore, every time a string is inserted, the root node will change. Each time, a new path will be opened. If the original points on this path exist, all the information of the original points will be cloned.
- Next, let's summarize how the insertion operation is carried out:
p = root[i - 1]; // p represents the root node of the previous version, the root node in the recursive process (that is, it may be a point in the middle)
q = root[i] = ++idx; // q represents the root node of the current version, which is also the root node in the recursive process
if (p) { // If p is not empty, the operation is required; otherwise, the first string is currently inserted
tr[q] = tr[p]; // Clone the nodes of the previous version to this version
}
// Assuming that the pointer of the current version points to the character si, you need to update the node where si is located
tr[q][si] = ++idx; // Open up a new point for si
p = tr[p][si], q = tr[q][si]; // Pointer down
// Until the current word traversal is completed
Persistence of segment tree
-
The persistence of segment tree is also called chairman tree.
-
Because there are multiple versions, the segment tree cannot be stored in heap mode, but in pointer mode. Here, the structure is used:
struct Node {
int l, r; // Not the left and right boundaries, but the subscripts of the left and right sons of the current node
// Some other information
}
- In addition, if we store the line segment tree in the way of pointer, we don't need to store the left and right boundaries. We can pass the left and right boundaries directly in the process of recursion
2. Persistent data structure on acwing
AcWing 256. Maximum XOR sum
Problem description
-
Question link: AcWing 256. Maximum XOR sum

analysis
- We define prefixes and S i S_i Si, the prefix sum of the first i numbers, and the first data is stored in a 1 a_1 In a1, i.e( ⨁ \bigoplus ⨁ indicates exclusive or):
S 0 = 0 S 1 = a 1 S 2 = a 1 ⨁ a 2 . . . S i = a 1 ⨁ a 2 ⨁ a 3 . . . . . . ⨁ a i S_0 = 0 \\ S_1 = a_1 \\ S_2 = a_1 \bigoplus a_2 \\ ... \\ S_i = a_1 \bigoplus a_2 \bigoplus a_3 ......\bigoplus a_i S0=0S1=a1S2=a1⨁a2...Si=a1⨁a2⨁a3......⨁ai
- After this definition, the content we need to solve can become:
a p ⨁ . . . . . . ⨁ a n ⨁ x = S p − 1 ⨁ S N ⨁ x a_p \bigoplus ......\bigoplus a_n \bigoplus x = S_{p-1} \bigoplus S_N \bigoplus x ap⨁......⨁an⨁x=Sp−1⨁SN⨁x
-
In the above formula, we can S N ⨁ x S_N \bigoplus x SN ⨁ x is regarded as a constant and recorded as C, which is equivalent to letting us in the interval [ L , R ] [L, R] Find a p in [L,R], so that S p − 1 ⨁ C S_{p-1} \bigoplus C The value of Sp − 1 ⨁ C is the maximum.
-
be similar to AcWing 143. Maximum XOR pair , for the explanation of this problem, please refer to: website . We can put each data a i a_i ai is regarded as a binary string because 0 ≤ a [ i ] ≤ 1 0 7 0 \le a[i] \le 10^7 0 ≤ a[i] ≤ 107, and 2 23 ≤ a [ i ] ≤ 2 24 2^{23} \le a[i] \le 2^{24} 223 ≤ a[i] ≤ 224, so we need to map each data to a 01 binary string with a length of 24.
-
We can consider a simple case first. Let's start with [ 1 , R ] [1, R] If we find such a p in [1,R], the problem is very similar to AcWing 143. Maximum XOR pair , the difference is that the a array in this question is constantly changing, so we need to record all historical versions of the trie tree. The trie tree formed by inserting a[1~R] is stored in root[R].
-
If the limit on the left of the interval is also added, the problem becomes that let's be in the interval [ L , R ] [L, R] Find a p in [L,R], so that S p − 1 ⨁ C S_{p-1} \bigoplus C The value of Sp − 1 ⨁ C is the largest. We can deal with it as follows: record one more information Max in each node in the trie tree_ ID, indicating the time t (i.e. the number of inserted) of the latest inserted data in the data represented by the subtree with the current node as the root, if t ≥ L t \ge L t ≥ L indicates that the subtree is [ L , R ] [L, R] [L,R] exists in this interval.
-
For A C mentioned above, data A can be regarded as A binary string of 24, traversing the string from left to right. Assuming that the character t is currently being investigated, we should go to the branch of 1^t in the trie tree (if it exists, that is, for the interval) [ L , R ] [L, R] [L,R], if Max corresponding to this branch_ id ≥ \ge ≥ L indicates existence), so that the XOR value can be maximized (greedy thought).
code
- C++
#include <iostream>
using namespace std;
const int N = 600010, M = N * 25;
int n, m; // Initial length of sequence and number of operations
int s[N]; // XOR prefix and
int tr[M][2]; // Nodes in trie
int max_id[M]; // The latest inserted data in the data represented by the subtree with the current node as the root, the insertion time t (i.e. the number of inserted data)
int root[N], idx; // Record each version, starting with 1
// i: Prefix and subscript, indicating the insertion of Si
// k: Which bit of Si is currently processed, starting from 23 to 0
// p: Root node of previous version
// q: The root node of the current version is a copy of p. the difference is that a new chain is added
void insert(int i, int k, int p, int q) {
if (k < 0) { // It means that we have processed the last bit (bit 0), and at this time q is the number of leaf nodes
max_id[q] = i;
return;
}
int v = s[i] >> k & 1;
// For all nodes that need to be modified, do not modify it, but copy a new one, and then modify the new point.
if (p) tr[q][v ^ 1] = tr[p][v ^ 1]; // If the previous version exists, copy it directly
tr[q][v] = ++idx; // At present, this binary bit needs to open up a new node
insert(i, k - 1, tr[p][v], tr[q][v]);
max_id[q] = max(max_id[tr[q][0]], max_id[tr[q][1]]); // The left and right sons are older
}
// Starting from root, the data to be XORed is C, and the left endpoint of the interval is L
int query(int root, int C, int L) {
int p = root;
for (int i = 23; i >= 0; i--) {
int v = C >> i & 1;
if (max_id[tr[p][v ^ 1]] >= L) p = tr[p][v ^ 1];
else p = tr[p][v]; // I can't find a better one. I can only make do with it
}
return C ^ s[max_id[p]]; // This leaf node has only itself, so max_id is the subscript i of Si
}
int main() {
scanf("%d%d", &n, &m);
// Here, max_ 0 in ID [0] indicates an empty node, which does not contain any points,
// So its max_id needs to be set to a number smaller than all IDS, so it can be set to any negative number.
max_id[0] = -1;
root[0] = ++idx; // The root node number of version 0 in trie is 1
insert(0, 23, 0, root[0]); // Insert S0 in version 0. There is no previous version
for (int i = 1; i <= n; i++) {
int x;
scanf("%d", &x);
s[i] = s[i - 1] ^ x;
root[i] = ++idx; // Version i
insert(i, 23, root[i - 1], root[i]);
}
char op[2];
int l, r, x;
for (int i = 1; i <= m; i++) {
scanf("%s", op);
if (*op == 'A') {
scanf("%d", &x);
n++;
s[n] = s[n - 1] ^ x;
root[n] = ++idx;
insert(n, 23, root[n - 1], root[n]);
} else {
scanf("%d%d%d", &l, &r, &x);
// p is between [L, R], and p-1 is between [L-1, R-1]
printf("%d\n", query(root[r - 1], s[n] ^ x, l - 1));
}
}
return 0;
}
AcWing 255. The K-th decimal
Problem description
-
Question link: AcWing 255. The K-th decimal

analysis
-
This is a super classic topic. This is a static problem (the original array will not change during the operation). You can solve it using the following methods:
(1) Merge tree, time complexity: O ( n × l o g 3 ( n ) ) O(n \times log^3(n)) O(n×log3(n));
(2) Partition tree, time complexity: O ( n × l o g ( n ) ) O(n \times log(n)) O(n × log(n)), space complexity: O ( n × l o g ( n ) ) O(n \times log(n)) O(n × log(n)); Can only solve this problem. It does not support the modification of the k-th decimal in the interval.
(3) Tree nesting, time complexity: O ( n × l o g 2 ( n ) ) O(n \times log^2(n)) O(n × log2(n)), spatial complexity: O ( n × l o g ( n ) ) O(n \times log(n)) O(n × log(n)); Here, the segment tree is used to set the balance tree. Each node in the segment tree is a balance tree, and the balance tree maintains an ordered sequence of intervals. The advantage of this data structure is that it supports the modification of the k-th decimal in the interval.
(4) Persistent segment tree (Chairman tree), time complexity: O ( n × l o g ( n ) ) O(n \times log(n)) O(n × log(n)), space complexity: O ( n × l o g ( n ) ) O(n \times log(n)) O(n × log(n)); It does not support the modification of the k-th decimal in the interval.
-
Choose (4) to solve this problem. The steps are as follows:
(1) Order preserving discretization;
(2) Establish a segment tree on the discretized values and maintain the total number of segments in each interval (the number represented by the right of the interval is greater than that on the left of the interval);
-
Find the k-th decimal of all data:

-
Suppose the input data is stored in array a, a[1] stores the first data, and now find the k-th decimal between a[L~R]. How should we deal with it? At the beginning, root[0] indicates the segment tree without any data inserted, that is, the 0th version. The root node of the segment tree after inserting the kth number is stored in root[i], that is, the ith version;
-
Find the k-th decimal point between a[L~R], we can find the root node of the r-th version of the line segment tree root[R]. If we find the k-th smallest number in root[R], the search result is the k-th smallest number in the first R.
-
We need to consider the left boundary L. for each version of the segment tree, the structure is exactly the same, but the stored information is different; Similar to the idea of prefix sum, we consider root[L-1]. If the number of elements in an interval [left, right] of this version is CNT2 and the number of elements in the corresponding interval [left, right] of root[R] is cnt1, cnt1-cnt2 represents the number of occurrences in the interval [left, right] from the L-th number to the r-th number.
-
Finally, consider how much space the line segment tree should open. There are at most N = 1 0 5 N=10^5 N=105 data. Each time a data is inserted, a version of information will be recorded, and a length of ⌈ N ⌉ = 17 \lceil N \rceil=17 ⌈ N ⌉ = 17 paths, so the required space size is N × 4 + N × 17 N \times 4 + N \times 17 N×4+N×17.
code
- C++
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 100010;
int n, m; // Sequence length and number of queries
int a[N]; // sequence
vector<int> nums; // Order preserving discrete array
struct Node {
int l, r; // Subscripts of the left and right sons of the current node
int cnt; // Number of data with data range of [num [l], Num [R]]
} tr[N * 4 + N * 17];
int root[N], idx;
// Returns the corresponding subscript of data x after discretization
int find(int x) {
return lower_bound(nums.begin(), nums.end(), x) - nums.begin();
}
// l: Left end point of interval, r: right end point of interval
// Returns the root node of the segment tree with interval [l, r]
int build(int l, int r) {
int p = ++idx; // Assign node to current node
if (l == r) return p;
int mid = l + r >> 1;
tr[p].l = build(l, mid), tr[p].r = build(mid + 1, r);
return p;
}
// p: The root node of the previous version of the segment tree
// l. r: a node of the segment tree corresponds to the left end point and the right end point of the interval
// x: Single point modification of the x-th number in the line segment tree
// Returns the root node of the new version segment tree
int insert(int p, int l, int r, int x) {
int q = ++idx;
tr[q] = tr[p];
if (l == r) {
tr[q].cnt++;
return q;
}
int mid = l + r >> 1;
if (x <= mid) tr[q].l = insert(tr[p].l, l, mid, x);
else tr[q].r = insert(tr[p].r, mid + 1, r, x);
tr[q].cnt = tr[tr[q].l].cnt + tr[tr[q].r].cnt;
return q;
}
// Returns the k-th smallest version between versions (p, q)
// The corresponding interval of the currently traversed segment tree is [l, r]
int query(int p, int q, int l, int r, int k) {
if (l == r) return r;
int cnt = tr[tr[q].l].cnt - tr[tr[p].l].cnt; // Number of left child data
int mid = l + r >> 1;
if (k <= cnt) return query(tr[p].l, tr[q].l, l, mid, k);
else return query(tr[p].r, tr[q].r, mid + 1, r, k - cnt);
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
nums.push_back(a[i]);
}
// Order preserving discretization
sort(nums.begin(), nums.end());
nums.erase(unique(nums.begin(), nums.end()), nums.end());
// No data corresponding to version 0 was inserted
root[0] = build(0, nums.size() - 1);
// Build segment tree of each version
for (int i = 1; i <= n; i++)
root[i] = insert(root[i - 1], 0, nums.size() - 1, find(a[i]));
while (m--) {
int l, r, k;
scanf("%d%d%d", &l, &r, &k);
printf("%d\n", nums[query(root[l - 1], root[r], 0, nums.size() - 1, k)]);
}
return 0;
}