Priority queues and heaps
Priority Queue
Ordinary queue: first in, first out, last in, then out
Priority queue: The queue order has nothing to do with the queue order; it has something to do with priority; (e.g. hospital queue and operating system dynamically select the highest priority task execution)
Graphics: keyword "dynamic"; the elements in the queue are constantly changing, and new elements are constantly entering the queue, not only in order of priority; [Priority can be specifically defined]
Distinction from ordinary queue: Outgoing element is the element with the highest priority, and the head element is also the element with the highest priority, not the element that first enters the queue.

II. Reactor Infrastructure
1. Binary Heap
The conditions for binary heap: binary heap is a complete binary tree; complete binary tree: arrange the elements in order to form a tree; [the bottom layer is all leaf nodes, but there may be leaf nodes above the last layer, but these leaf nodes must be all on the right side of the tree]
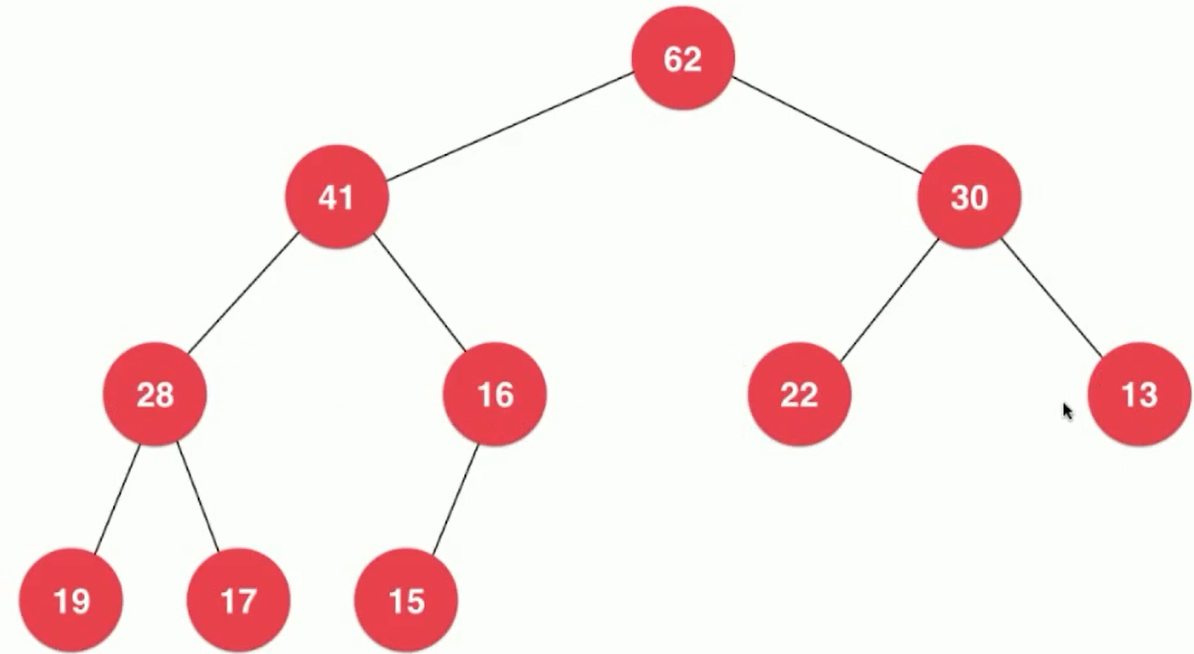
The nature of binary heap: [There is no necessary connection between node size and its hierarchy]
1. Maximum heap: The value of a node in the heap is always less than that of its parent; [The value of the father node is greater than that of the left and right children]
2. Minimum heap: The value of a node in the heap is always greater than that of its parent; [The value of the father node is less than that of the left and right children]
Complete binary trees can be implemented with arrays:
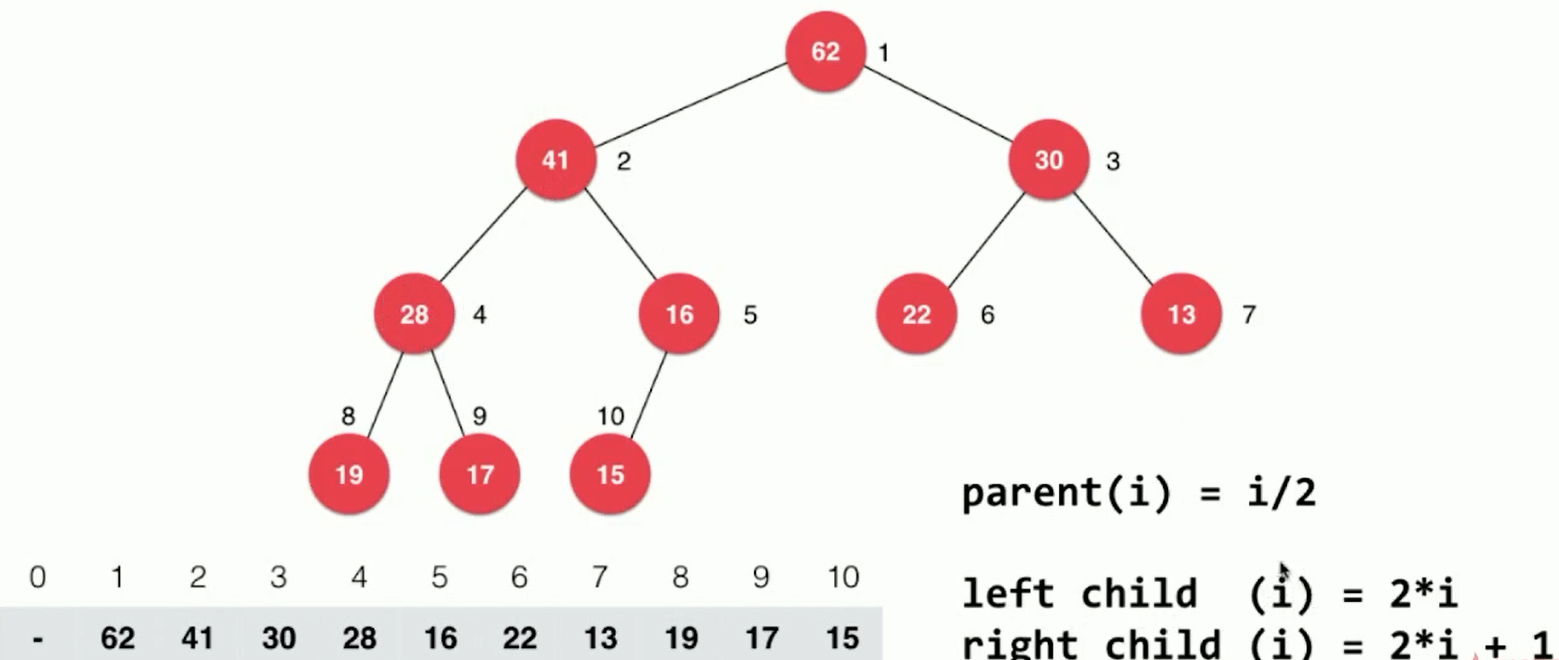
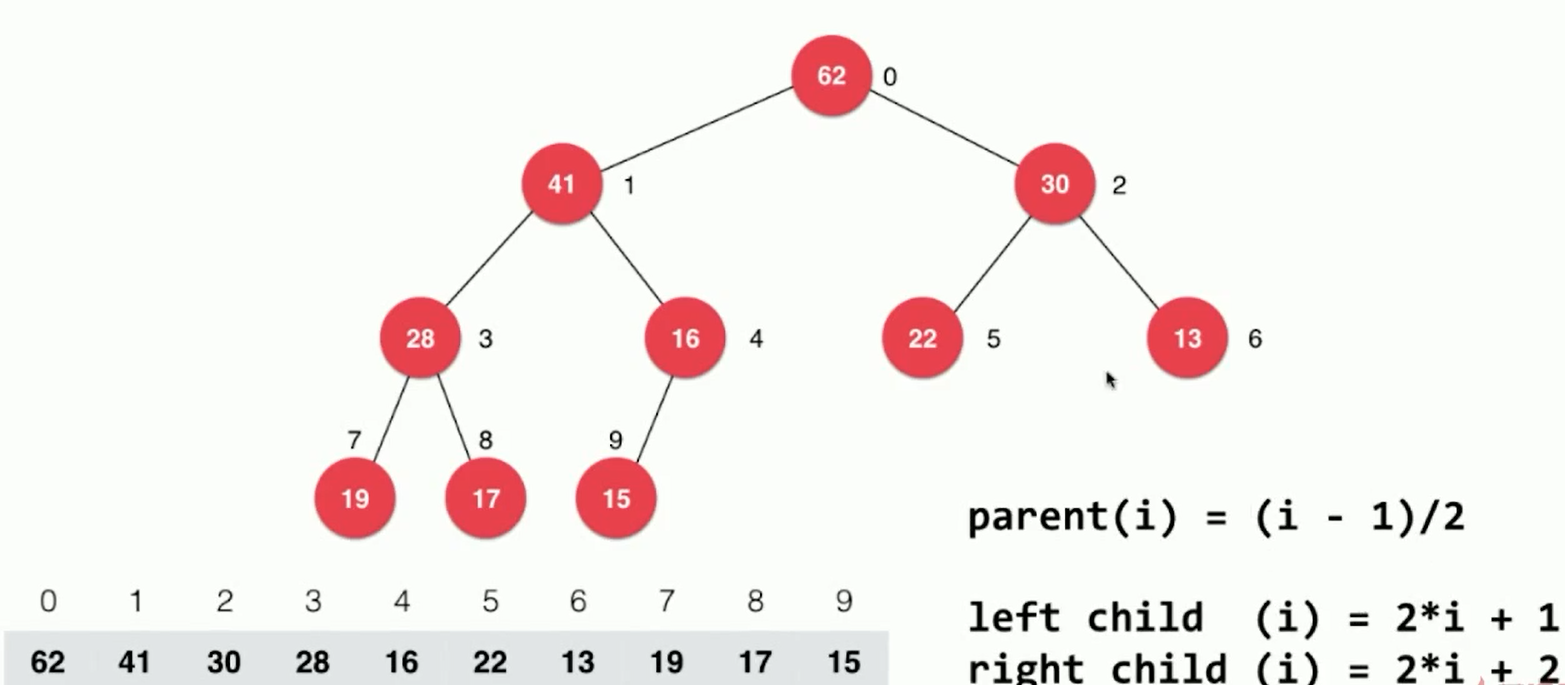
Code implementation: MaxHeap.java
public class MaxHeap<E extends Comparable<E>> { //Comparable
private Array<E> data;
public MaxHeap(int capacity){
data = new Array<>(capacity);
}
public MaxHeap(){
data = new Array<>();
}
// Returns the number of elements in the heap
public int size(){
return data.getSize();
}
// Returns a Boolean value indicating whether the heap is empty
public boolean isEmpty(){
return data.isEmpty();
}
// Returns the index of the parent node of the element represented by an index in the array representation of a complete binary tree
private int parent(int index){
if(index == 0) //Root node, no father node
throw new IllegalArgumentException("index-0 doesn't have parent.");
return (index - 1) / 2;
}
// Returns the index of the left child node of the element represented by an index in the array representation of a complete binary tree
private int leftChild(int index){
return index * 2 + 1;
}
// Returns the index of the right child node of the element represented by an index in the array representation of a complete binary tree
private int rightChild(int index){
return index * 2 + 2;
}
}
3. Adding elements to the heap
Sift up in heap
1. Add element 52 to the heap
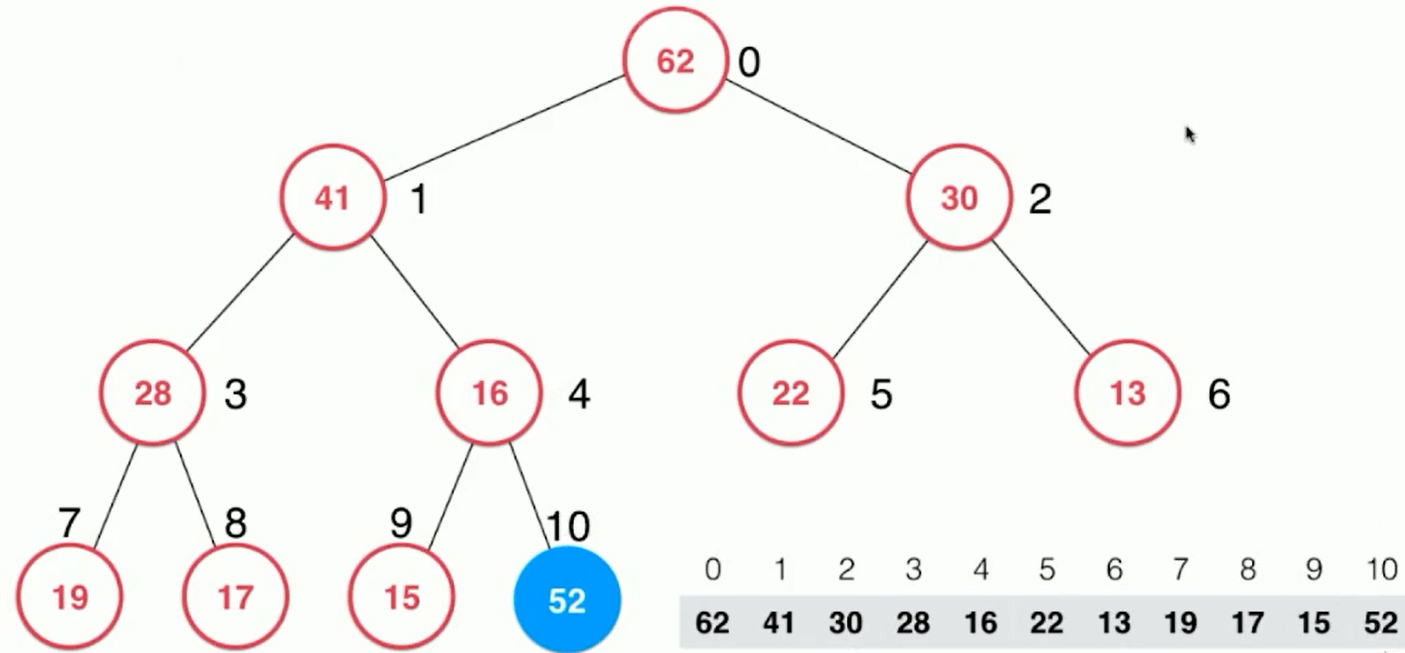
2. After adding 52, 52 > 16, the father node is not satisfied with the condition, and the child node is not satisfied with the condition. It should be adjusted to compare with the father node all the way from 52 and exchange the order.
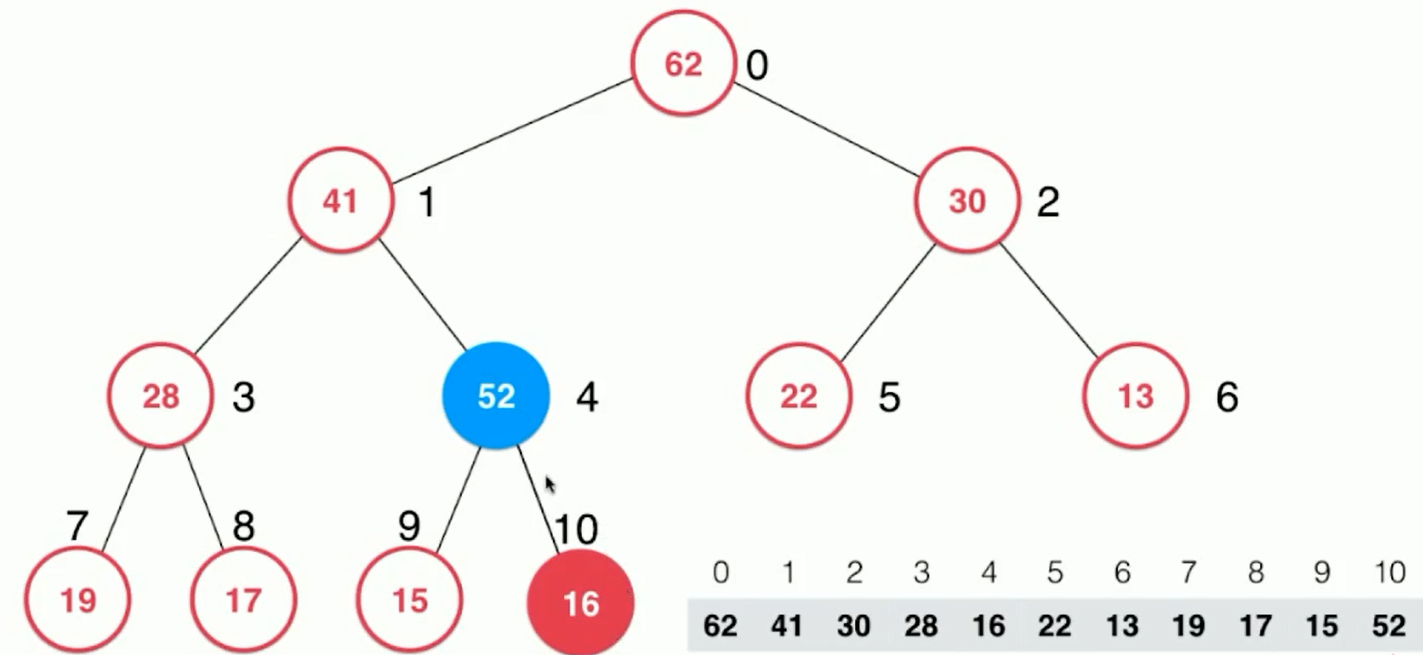
Exchange 52 with 16 in order; but 52 > 41, continue exchanging positions
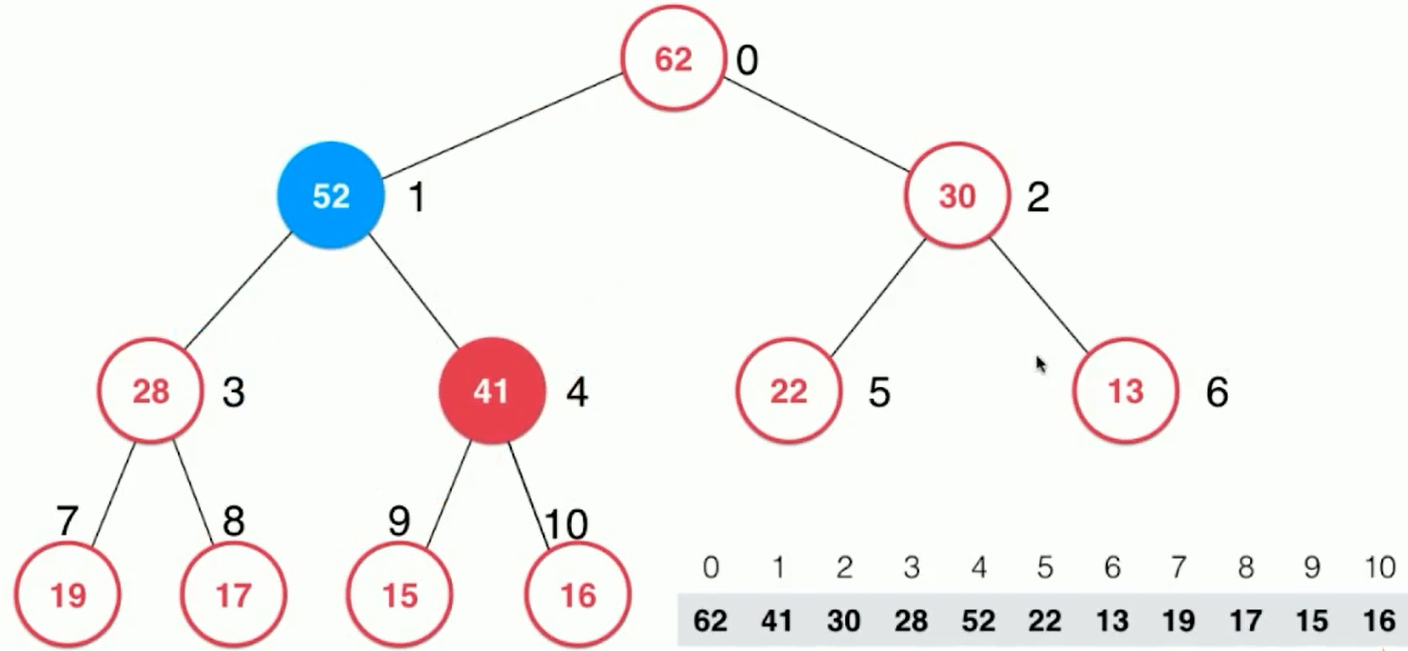
At this time, 62 > 52, which conforms to the nature of the heap.
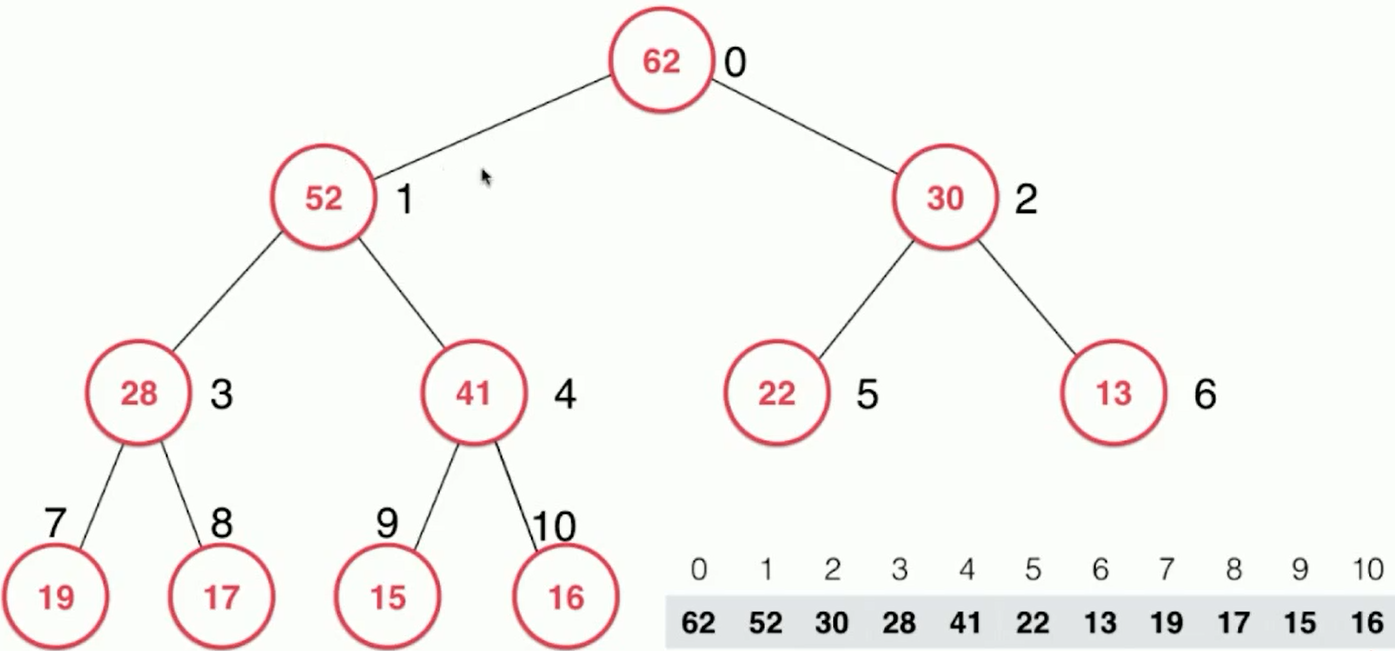
Sift up in the heap: 52 floats gradually from the bottom until it is in its proper position to maintain the nature of the heap.
Code implementation:
MaxHeap.java
public class MaxHeap<E extends Comparable<E>> {
private Array<E> data;
public MaxHeap(int capacity){
data = new Array<>(capacity);
}
public MaxHeap(){
data = new Array<>();
}
// Returns the number of elements in the heap
public int size(){
return data.getSize();
}
// Returns a Boolean value indicating whether the heap is empty
public boolean isEmpty(){
return data.isEmpty();
}
// Returns the index of the parent node of the element represented by an index in the array representation of a complete binary tree
private int parent(int index){
if(index == 0)
throw new IllegalArgumentException("index-0 doesn't have parent.");
return (index - 1) / 2;
}
// Returns the index of the left child node of the element represented by an index in the array representation of a complete binary tree
private int leftChild(int index){
return index * 2 + 1;
}
// Returns the index of the right child node of the element represented by an index in the array representation of a complete binary tree
private int rightChild(int index){
return index * 2 + 2;
}
// Adding elements to the heap (new code)
public void add(E e){
data.addLast(e);
siftUp(data.getSize() - 1);
}
private void siftUp(int k){
while(k > 0 && data.get(parent(k)).compareTo(data.get(k)) < 0 ){
//K's father element is compared with K's. If the father element is smaller, the two exchange positions.
data.swap(k, parent(k)); //swap method for k and k father element exchange
k = parent(k);
}
}
}
Array.java
public class Array<E> {
private E[] data;
private int size;
// Constructor, capacity capacity of the incoming array constructs Array
public Array(int capacity){
data = (E[])new Object[capacity];
size = 0;
}
// No parameter constructor, default array capacity=10
public Array(){
this(10);
}
// Capture the capacity of an array
public int getCapacity(){
return data.length;
}
// Gets the number of elements in an array
public int getSize(){
return size;
}
// Whether the return array is empty
public boolean isEmpty(){
return size == 0;
}
// Insert a new element e at the index location
public void add(int index, E e){
if(index < 0 || index > size)
throw new IllegalArgumentException("Add failed. Require index >= 0 and index <= size.");
if(size == data.length)
resize(2 * data.length);
for(int i = size - 1; i >= index ; i --)
data[i + 1] = data[i];
data[index] = e;
size ++;
}
// Add a new element to all elements
public void addLast(E e){
add(size, e);
}
// Add a new element before all elements
public void addFirst(E e){
add(0, e);
}
// Get the element of index index index location
public E get(int index){
if(index < 0 || index >= size)
throw new IllegalArgumentException("Get failed. Index is illegal.");
return data[index];
}
// Modify the index index location to e
public void set(int index, E e){
if(index < 0 || index >= size)
throw new IllegalArgumentException("Set failed. Index is illegal.");
data[index] = e;
}
// Find if there is an element e in the array
public boolean contains(E e){
for(int i = 0 ; i < size ; i ++){
if(data[i].equals(e))
return true;
}
return false;
}
// Find the index of the element e in the array, and return - 1 if there is no element e
public int find(E e){
for(int i = 0 ; i < size ; i ++){
if(data[i].equals(e))
return i;
}
return -1;
}
// Remove the element in the index position from the array and return the deleted element
public E remove(int index){
if(index < 0 || index >= size)
throw new IllegalArgumentException("Remove failed. Index is illegal.");
E ret = data[index];
for(int i = index + 1 ; i < size ; i ++)
data[i - 1] = data[i];
size --;
data[size] = null; // loitering objects != memory leak
if(size == data.length / 4 && data.length / 2 != 0)
resize(data.length / 2);
return ret;
}
// Delete the first element from the array and return the deleted element
public E removeFirst(){
return remove(0);
}
// Delete the last element from the array and return the deleted element
public E removeLast(){
return remove(size - 1);
}
// Delete element e from the array
public void removeElement(E e){
int index = find(e);
if(index != -1)
remove(index);
}
public void swap(int i, int j){
if(i < 0 || i >= size || j < 0 || j >= size)
throw new IllegalArgumentException("Index is illegal.");
E t = data[i];
data[i] = data[j];
data[j] = t;
}
@Override
public String toString(){
StringBuilder res = new StringBuilder();
res.append(String.format("Array: size = %d , capacity = %d\n", size, data.length));
res.append('[');
for(int i = 0 ; i < size ; i ++){
res.append(data[i]);
if(i != size - 1)
res.append(", ");
}
res.append(']');
return res.toString();
}
// Change the capacity of array space to the size of new Capacity
private void resize(int newCapacity){
E[] newData = (E[])new Object[newCapacity];
for(int i = 0 ; i < size ; i ++)
newData[i] = data[i];
data = newData;
}
}
4. Extracting elements from the heap
Extract the element, only take out the heap top element (the root node of the binary tree), which is the largest element stored in the binary tree.
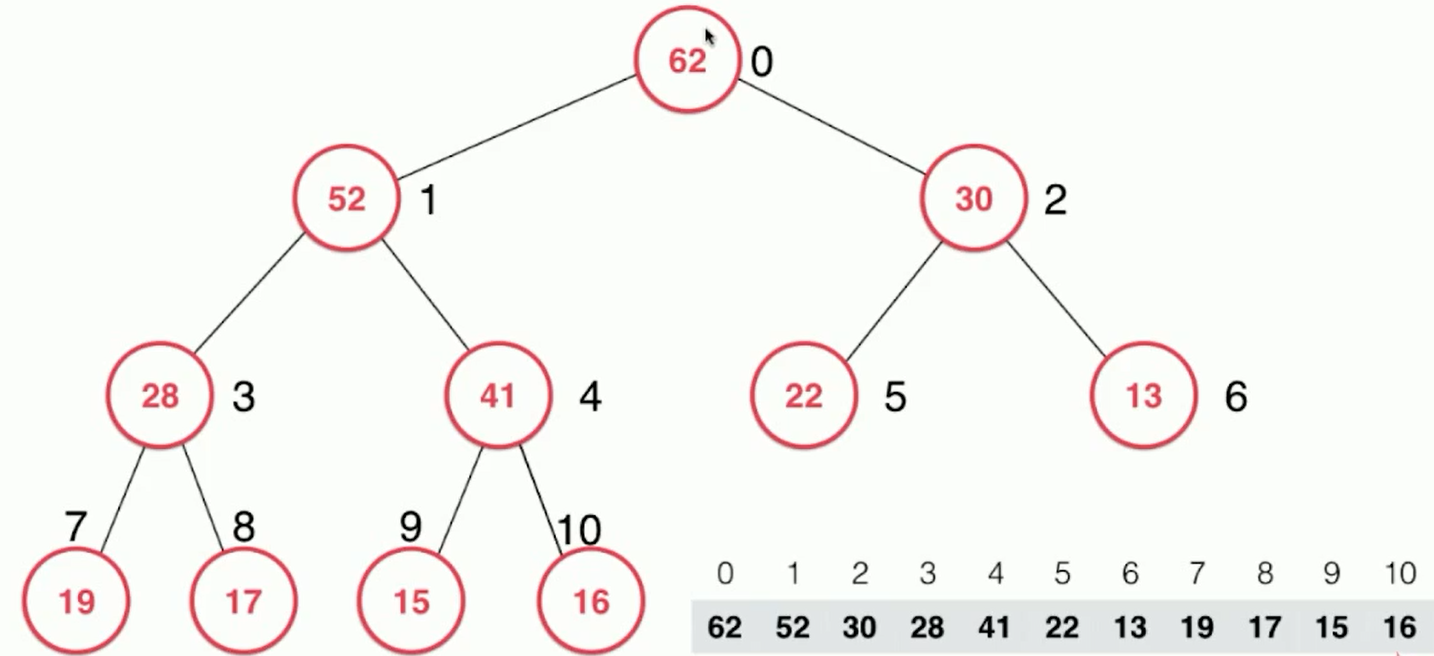
Procedure: 1. Access the root node, the elements with index 0 in the array; take it away, for the whole heap, it can be seen as having two subtrees;
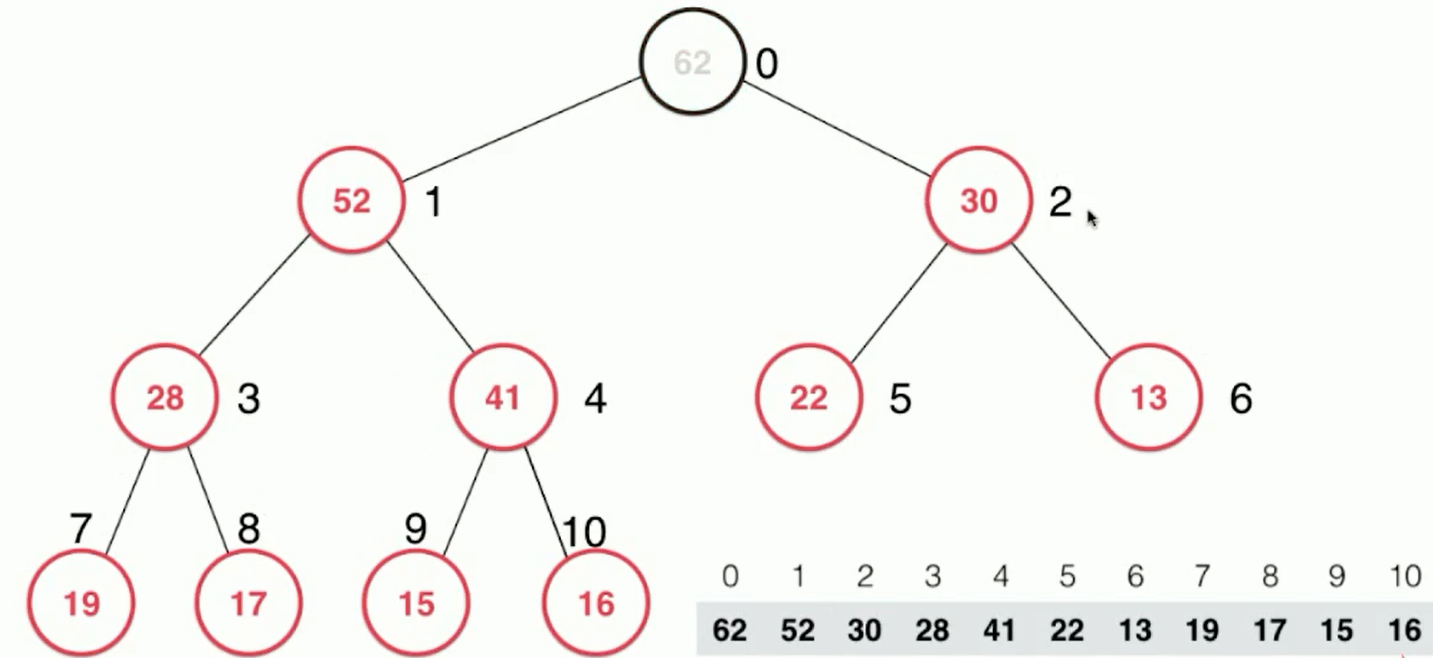
2. Top the last element (16) of the heap to the top of the heap; change the array 0 to 16 and delete the corresponding 16 of the array 10
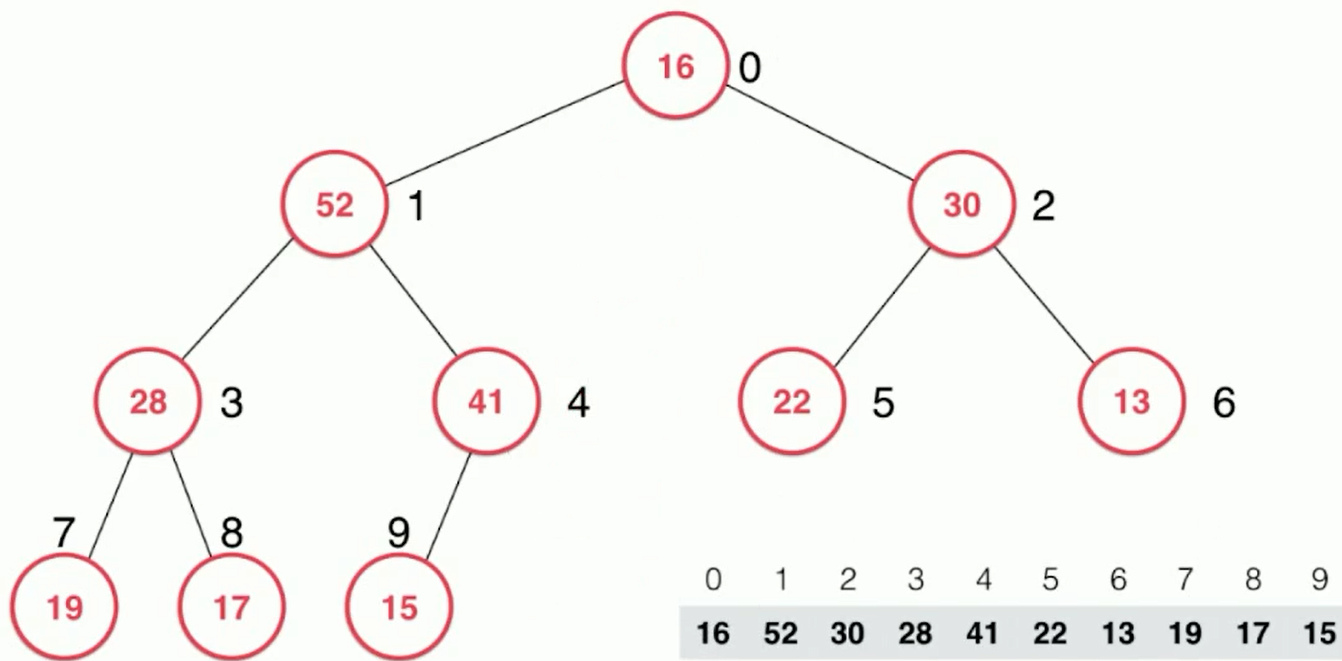
3. But if 16 is on the top of the heap, it breaks the nature of the heap, 16 < 52 < 30, which does not conform to the nature that the father node in the heap is larger than the left and right children.
Sift Down: Elements sink in the heap;
The sinking process 1. The father node was compared with the left and right children (16 compared with 52 and 30);
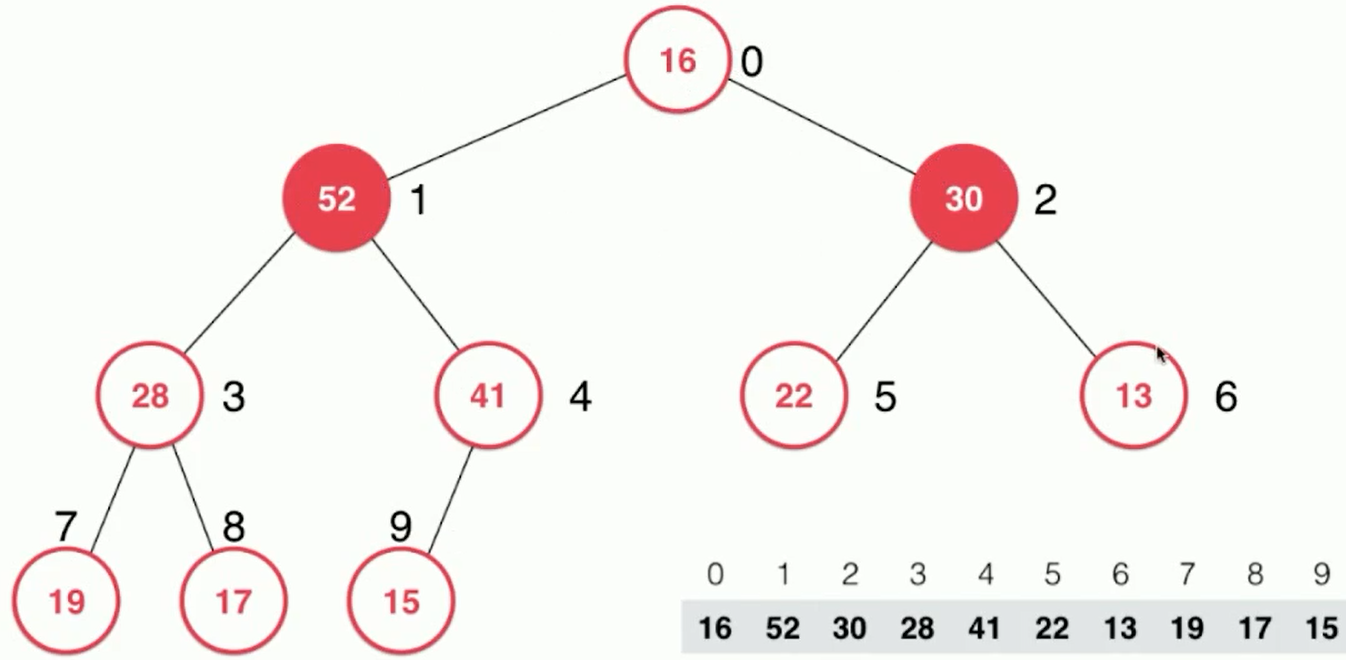
2. Choose the bigger elements in children and exchange positions.
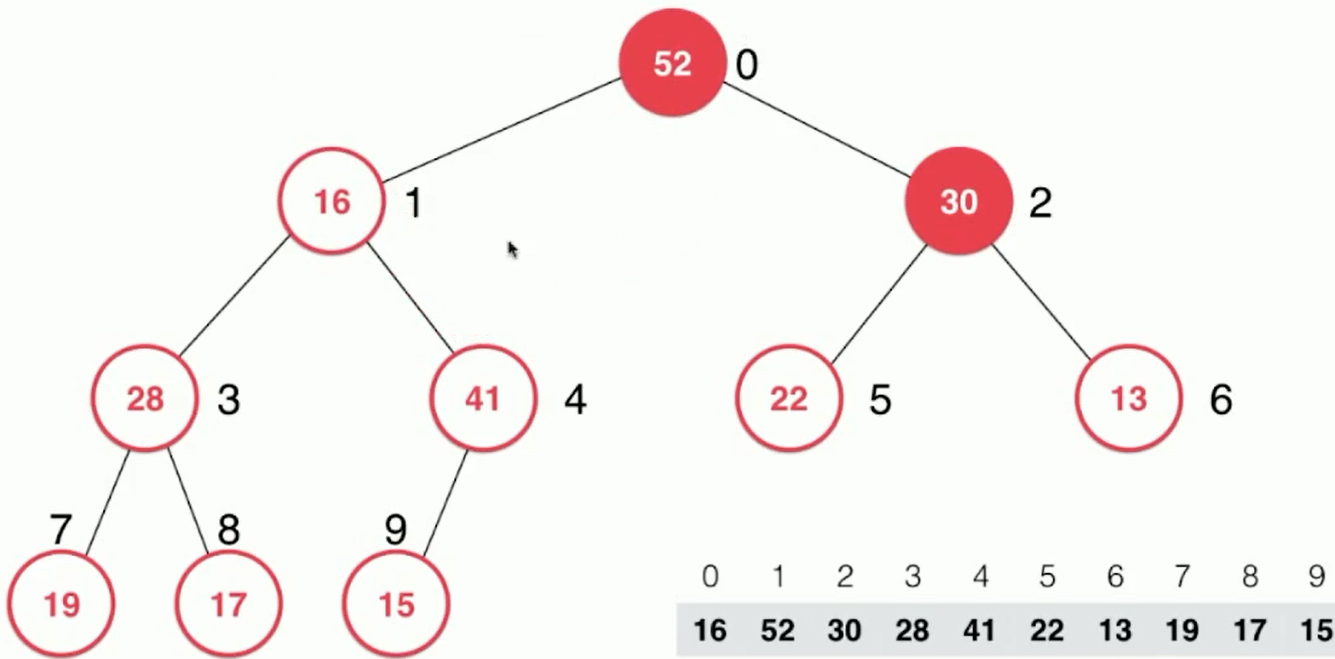
3. The father node continues to compare with the left and right children, repeating the steps above.
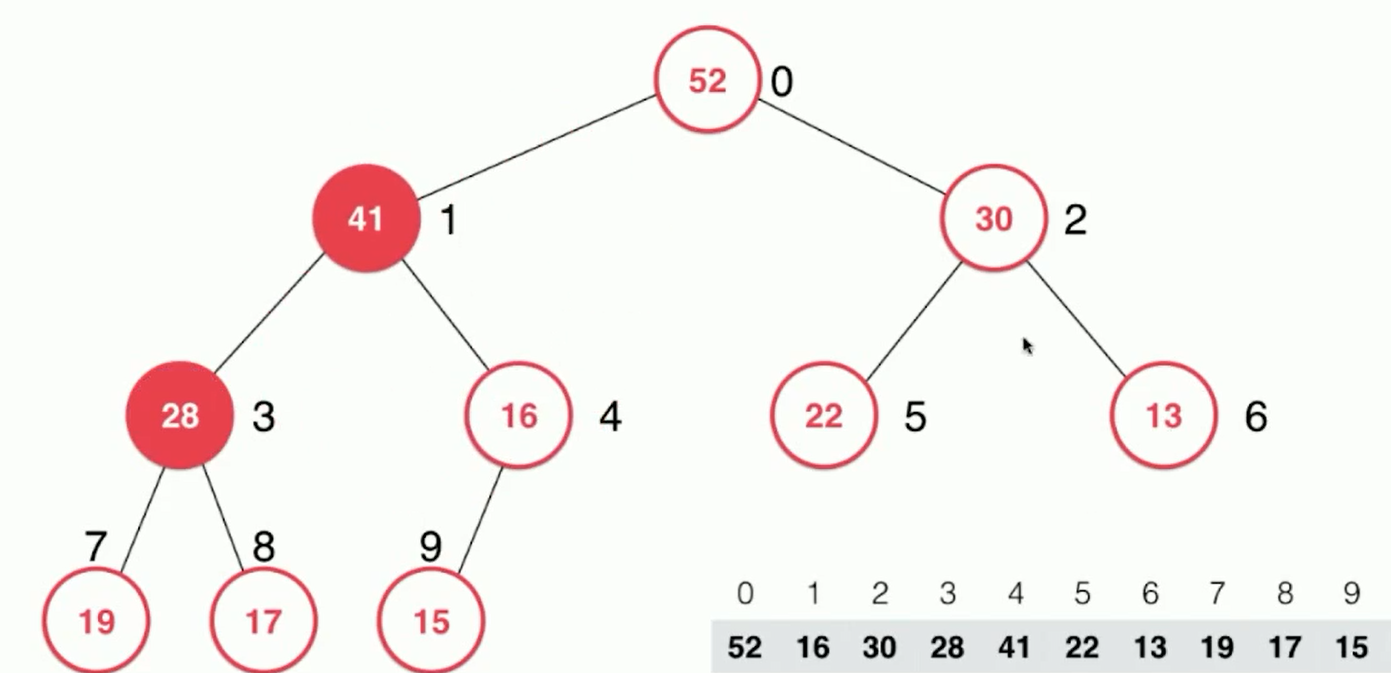
4.16 > 15, satisfying the nature of the heap, the final shape is shown below.
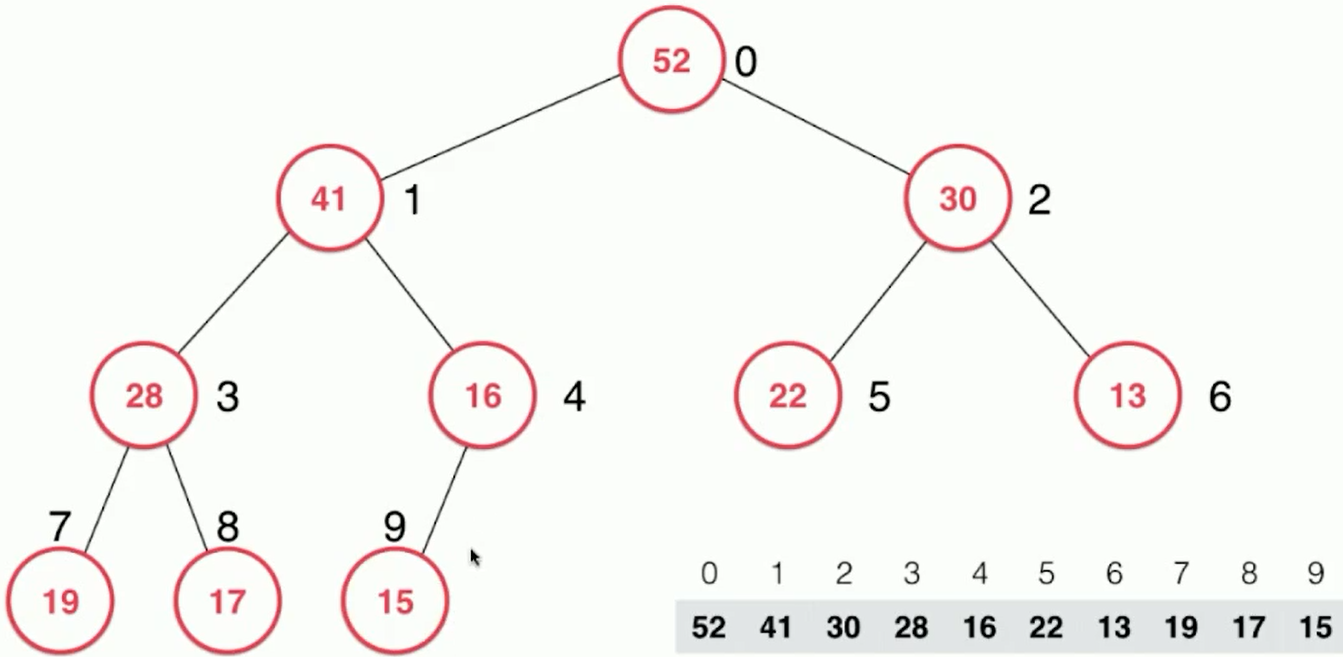
Code implementation: MaxHeap.java
public class MaxHeap<E extends Comparable<E>> {
private Array<E> data;
public MaxHeap(int capacity){
data = new Array<>(capacity);
}
public MaxHeap(){
data = new Array<>();
}
// Returns the number of elements in the heap
public int size(){
return data.getSize();
}
// Returns a Boolean value indicating whether the heap is empty
public boolean isEmpty(){
return data.isEmpty();
}
// Returns the index of the parent node of the element represented by an index in the array representation of a complete binary tree
private int parent(int index){
if(index == 0)
throw new IllegalArgumentException("index-0 doesn't have parent.");
return (index - 1) / 2;
}
// Returns the index of the left child node of the element represented by an index in the array representation of a complete binary tree
private int leftChild(int index){
return index * 2 + 1;
}
// Returns the index of the right child node of the element represented by an index in the array representation of a complete binary tree
private int rightChild(int index){
return index * 2 + 2;
}
// Adding elements to the heap
public void add(E e){
data.addLast(e);
siftUp(data.getSize() - 1);
}
private void siftUp(int k){
while(k > 0 && data.get(parent(k)).compareTo(data.get(k)) < 0 ){
data.swap(k, parent(k));
k = parent(k);
}
}
// The largest element in the heap
public E findMax(){
if(data.getSize() == 0)
throw new IllegalArgumentException("Can not findMax when heap is empty.");
return data.get(0);
}
// Remove the largest element in the heap (new code)
public E extractMax(){
E ret = findMax();
data.swap(0, data.getSize() - 1);
data.removeLast(); //Delete the largest element
siftDown(0); //Subsidence operation, corresponding index is 0
return ret;
}
private void siftDown(int k){
while(leftChild(k) < data.getSize()){//The left child's index is smaller than the total number of elements in the array, and the k node has no children.
int j = leftChild(k); // In this cycle, data[k] and data[j] exchange locations
if( j + 1 < data.getSize() &&
data.get(j + 1).compareTo(data.get(j)) > 0 )
j ++; //j Storage is actually the index of the right child
// data[j] is the maximum in leftChild and rightChild
if(data.get(k).compareTo(data.get(j)) >= 0 ) //Comparing k with j, the biggest element in children
break;
data.swap(k, j); //If J > k, the positions of the two are exchanged
k = j;
}
}
}
Main. Java (test)
import java.util.Random;
public class Main {
public static void main(String[] args) {
int n = 1000000; //Number of random numbers
MaxHeap<Integer> maxHeap = new MaxHeap<>();
Random random = new Random();
for(int i = 0 ; i < n ; i ++)
maxHeap.add(random.nextInt(Integer.MAX_VALUE));//Sort 1000000 random numbers (from large to small)
int[] arr = new int[n];
for(int i = 0 ; i < n ; i ++)
arr[i] = maxHeap.extractMax();
for(int i = 1 ; i < n ; i ++)
if(arr[i-1] < arr[i]) //Compare adjacent numbers (right > left)
throw new IllegalArgumentException("Error");
System.out.println("Test MaxHeap completed.");
}
}
Output:
Time complexity analysis: The time complexity of add and extract Max is O(log n), [or the level of binary tree height, but for heap, because it is a complete binary tree, it will never become linked list form, there is no worst case of n].