Heap-based priority queue
I. Code Implementation
Queue.java
public interface Queue<E> {
int getSize();
boolean isEmpty();
void enqueue(E e);
E dequeue();
E getFront();
}
PriorityQueue.java
public class PriorityQueue<E extends Comparable<E>> implements Queue<E> {
private MaxHeap<E> maxHeap;
public PriorityQueue(){
maxHeap = new MaxHeap<>();
}
@Override
public int getSize(){
return maxHeap.size();
}
@Override
public boolean isEmpty(){
return maxHeap.isEmpty();
}
@Override
public E getFront(){ //Look at the team leader element
return maxHeap.findMax();
}
@Override
public void enqueue(E e){ //Entry operation, bring e element into the queue
maxHeap.add(e);
}
@Override
public E dequeue(){//Out-of-line operation (head element, extract maximum)
return maxHeap.extractMax();
}
}
Classical Questions of Priority Queue
Choose the first 100 elements from 100,000 elements [the first M elements from N elements, M < N]
Solution:
1. The time complexity of using advanced sorting (merging, etc.) is NlogN.
2. The time complexity of using priority queue is NlogM; (M < N)
The idea of using priority queue method: [using minimum heap]
Maintain the first M elements currently seen with the priority queue, put the first M elements of N elements into the priority queue, and then replace the smallest element in the priority queue with a new element whenever a new element is seen, if the new element is larger than the smallest element in the priority queue; until traversal. When all N elements are finished, the M elements left in them are the M elements we are looking for.
Specific issues:
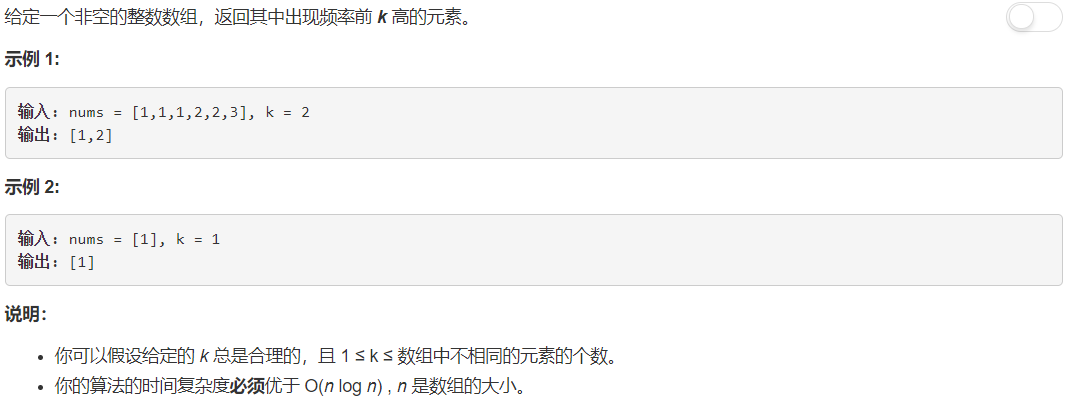
Code implementation:
Solution.java
import java.util.LinkedList;
import java.util.List;
import java.util.TreeMap;
class Solution {
private class Array<E> {
private E[] data;
private int size;
// Constructor, capacity capacity of the incoming array constructs Array
public Array(int capacity){
data = (E[])new Object[capacity];
size = 0;
}
// No parameter constructor, default array capacity=10
public Array(){
this(10);
}
public Array(E[] arr){
data = (E[])new Object[arr.length];
for(int i = 0 ; i < arr.length ; i ++)
data[i] = arr[i];
size = arr.length;
}
}
// Capture the capacity of an array
public int getCapacity(){
return data.length;
}
// Gets the number of elements in an array
public int getSize(){
return size;
}
// Whether the return array is empty
public boolean isEmpty(){
return size == 0;
}
// Insert a new element e at the index location
public void add(int index, E e){
if(index < 0 || index > size)
throw new IllegalArgumentException("Add failed. Require index >= 0 and index <= size.");
if(size == data.length)
resize(2 * data.length);
for(int i = size - 1; i >= index ; i --)
data[i + 1] = data[i];
data[index] = e;
size ++;
}
// Add a new element to all elements
public void addLast(E e){
add(size, e);
}
// Add a new element before all elements
public void addFirst(E e){
add(0, e);
}
// Get the element of index index index location
public E get(int index){
if(index < 0 || index >= size)
throw new IllegalArgumentException("Get failed. Index is illegal.");
return data[index];
}
// Modify the index index location to e
public void set(int index, E e){
if(index < 0 || index >= size)
throw new IllegalArgumentException("Set failed. Index is illegal.");
data[index] = e;
}
// Find if there is an element e in the array
public boolean contains(E e){
for(int i = 0 ; i < size ; i ++){
if(data[i].equals(e))
return true;
}
return false;
}
// Find the index of the element e in the array, and return - 1 if there is no element e
public int find(E e){
for(int i = 0 ; i < size ; i ++){
if(data[i].equals(e))
return i;
}
return -1;
}
// Remove the element in the index position from the array and return the deleted element
public E remove(int index){
if(index < 0 || index >= size)
throw new IllegalArgumentException("Remove failed. Index is illegal.");
E ret = data[index];
for(int i = index + 1 ; i < size ; i ++)
data[i - 1] = data[i];
size --;
data[size] = null; // loitering objects != memory leak
if(size == data.length / 4 && data.length / 2 != 0)
resize(data.length / 2);
return ret;
}
// Delete the first element from the array and return the deleted element
public E removeFirst(){
return remove(0);
}
// Delete the last element from the array and return the deleted element
public E removeLast(){
return remove(size - 1);
}
// Delete element e from the array
public void removeElement(E e){
int index = find(e);
if(index != -1)
remove(index);
}
public void swap(int i, int j){
if(i < 0 || i >= size || j < 0 || j >= size)
throw new IllegalArgumentException("Index is illegal.");
E t = data[i];
data[i] = data[j];
data[j] = t;
}
@Override
public String toString(){
StringBuilder res = new StringBuilder();
res.append(String.format("Array: size = %d , capacity = %d\n", size, data.length));
res.append('[');
for(int i = 0 ; i < size ; i ++){
res.append(data[i]);
if(i != size - 1)
res.append(", ");
}
res.append(']');
return res.toString();
}
// Change the capacity of array space to the size of new Capacity
private void resize(int newCapacity){
E[] newData = (E[])new Object[newCapacity];
for(int i = 0 ; i < size ; i ++)
newData[i] = data[i];
data = newData;
}
}
private class MaxHeap<E extends Comparable<E>> {
private Array<E> data;
public MaxHeap(int capacity){
data = new Array<>(capacity);
}
public MaxHeap(){
data = new Array<>();
}
public MaxHeap(E[] arr){
data = new Array<>(arr);
for(int i = parent(arr.length - 1) ; i >= 0 ; i --)
siftDown(i);
}
// Returns the number of elements in the heap
public int size(){
return data.getSize();
}
// Returns a Boolean value indicating whether the heap is empty
public boolean isEmpty(){
return data.isEmpty();
}
// Returns the index of the parent node of the element represented by an index in the array representation of a complete binary tree
private int parent(int index){
if(index == 0)
throw new IllegalArgumentException("index-0 doesn't have parent.");
return (index - 1) / 2;
}
// Returns the index of the left child node of the element represented by an index in the array representation of a complete binary tree
private int leftChild(int index){
return index * 2 + 1;
}
// Returns the index of the right child node of the element represented by an index in the array representation of a complete binary tree
private int rightChild(int index){
return index * 2 + 2;
}
// Adding elements to the heap
public void add(E e){
data.addLast(e);
siftUp(data.getSize() - 1);
}
private void siftUp(int k){
while(k > 0 && data.get(parent(k)).compareTo(data.get(k)) < 0 ){
data.swap(k, parent(k));
k = parent(k);
}
}
// The largest element in the heap
public E findMax(){
if(data.getSize() == 0)
throw new IllegalArgumentException("Can not findMax when heap is empty.");
return data.get(0);
}
// Remove the largest element from the heap
public E extractMax(){
E ret = findMax();
data.swap(0, data.getSize() - 1);
data.removeLast();
siftDown(0);
return ret;
}
private void siftDown(int k){
while(leftChild(k) < data.getSize()){
int j = leftChild(k); // In this cycle, data[k] and data[j] exchange locations
if( j + 1 < data.getSize() &&
data.get(j + 1).compareTo(data.get(j)) > 0 )
j ++;
// data[j] is the maximum in leftChild and rightChild
if(data.get(k).compareTo(data.get(j)) >= 0 )
break;
data.swap(k, j);
k = j;
}
}
// Take out the largest element in the heap and replace it with element e
public E replace(E e){
E ret = findMax();
data.set(0, e);
siftDown(0);
return ret;
}
}
private interface Queue<E> {
int getSize();
boolean isEmpty();
void enqueue(E e);
E dequeue();
E getFront();
}
private class PriorityQueue<E extends Comparable<E>> implements Queue<E> {
private MaxHeap<E> maxHeap;
public PriorityQueue(){
maxHeap = new MaxHeap<>();
}
@Override
public int getSize(){
return maxHeap.size();
}
@Override
public boolean isEmpty(){
return maxHeap.isEmpty();
}
@Override
public E getFront(){
return maxHeap.findMax();
}
@Override
public void enqueue(E e){
maxHeap.add(e);
}
@Override
public E dequeue(){
return maxHeap.extractMax();
}
}
private class Freq implements Comparable<Freq>{
public int e, freq;
public Freq(int e, int freq){
this.e = e;
this.freq = freq;
}
@Override
public int compareTo(Freq another){
if(this.freq < another.freq)
return 1;
else if(this.freq > another.freq)
return -1;
else
return 0;
}
}
public List<Integer> topKFrequent(int[] nums, int k) { //Statistical frequency
TreeMap<Integer, Integer> map = new TreeMap<>();
for(int num: nums){
if(map.containsKey(num))
map.put(num, map.get(num) + 1);
else
map.put(num, 1);
}
PriorityQueue<Freq> pq = new PriorityQueue<>();//Using Priority Queue to Find the First K Elements
for(int key: map.keySet()){
if(pq.getSize() < k)
pq.enqueue(new Freq(key, map.get(key)));
else if(map.get(key) > pq.getFront().freq){
pq.dequeue();
pq.enqueue(new Freq(key, map.get(key)));
}
}
LinkedList<Integer> res = new LinkedList<>();
//Put the elements in the priority queue back in LinkedList
while(!pq.isEmpty())
res.add(pq.dequeue().e);
return res;
}Output success:

Method 2: Use the priority queue in the Java standard library
Code: Solution.java
import java.util.LinkedList;
import java.util.List;
import java.util.PriorityQueue;
import java.util.TreeMap;
public class Solution {
private class Freq implements Comparable<Freq>{
public int e, freq;
public Freq(int e, int freq){
this.e = e;
this.freq = freq;
}
public int compareTo(Freq another){
if(this.freq < another.freq)
return -1;
else if(this.freq > another.freq)
return 1;
else
return 0;
}
}
public List<Integer> topKFrequent(int[] nums, int k) {
TreeMap<Integer, Integer> map = new TreeMap<>();
for(int num: nums){
if(map.containsKey(num))
map.put(num, map.get(num) + 1);
else
map.put(num, 1);
}
PriorityQueue<Freq> pq = new PriorityQueue<>();
for(int key: map.keySet()){
if(pq.size() < k)
pq.add(new Freq(key, map.get(key)));
else if(map.get(key) > pq.peek().freq){
pq.remove();
pq.add(new Freq(key, map.get(key)));
}
}
LinkedList<Integer> res = new LinkedList<>();
while(!pq.isEmpty())
res.add(pq.remove().e);
return res;
}
}Supplement:
D-ary heap
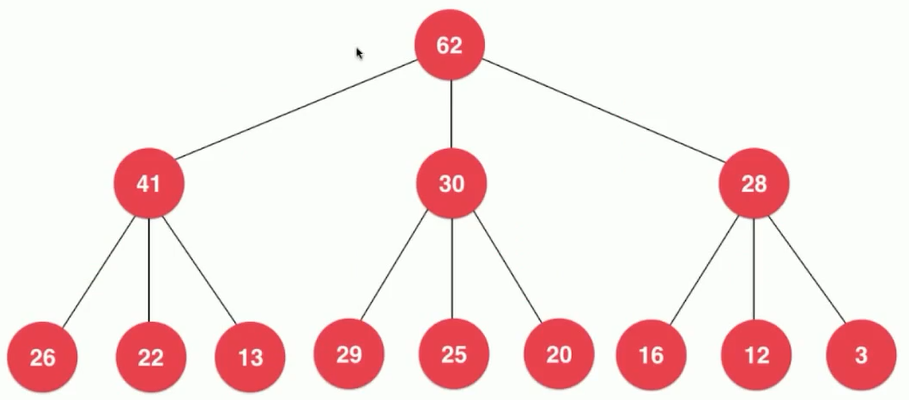
2. Index heap: You can quickly know the location of an element in the heap by indexing and modify it.
3. Generalized Queue
Queues can be called as long as they support entry and exit operations.
Ordinary queue: FIFO, FIFO
Priority Queue: A queue with the highest priority element as the outgoing element [Stack can also be understood as a queue]