red-black tree
The clearest explanation of red and black trees in history (I)
The clearest explanation of red and black trees in history (Part II)
I. Overview
Diagram:
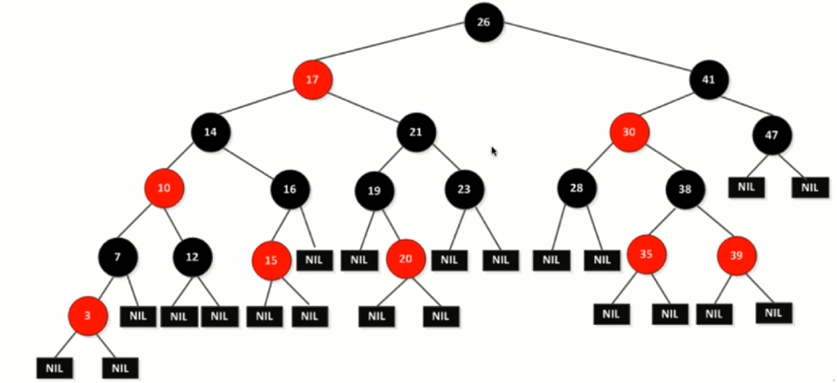
The red-black tree is a binary search tree, and some properties are added on the basis of the binary search tree to ensure that it does not degenerate into a linked list and that it is a balanced binary tree.
Specific provisions in Introduction to Algorithms:
1. Each node is either red or black.
2. The root node is black.
3. Each leaf node (the last empty node) is black.
4. If a node is red, then both of its child nodes are black.
5. From any node to the leaf node (the last empty node), the black node passes through is the same.
To better understand red and black trees, you need to know what 2-3 trees are.
2-3 Trees
1. Satisfying the Basic Properties of Binary Search Tree
2. Not a binary tree, it has two nodes, one can store one element [left child < a < right child], the other can store two elements [three children, left child < B < middle child < C < right child].
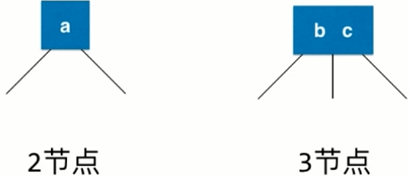
3. Each node has two or three children, so it is called a 2-3 tree.
Diagram:
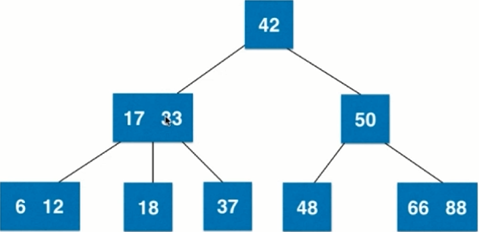
2-3 Tree Property: It is an absolutely balanced tree [the number of nodes passing from root node to any leaf node must be the same, and the height of left and right subtrees must be the same for any node].
How Trees Maintain Absolute Balance
Adding Nodes to 2-3 Trees
1. 42 is the root node

2. Add element 37, because 37 < 42, so 37 should be placed in the left subtree of 42. Because the left subtree of 42 is empty, new node 37 will be fused to the last leaf node found in the adding process. The node is 42, so the fusion of nodes will occur, from 2 nodes to 3 nodes.

3. Adding element 12, because 12 < 37, so 12 should be placed in the left subtree of 37. Because the left subtree of 37 is empty (the new node will never go empty, but will merge with the last leaf node), although it is already 3 nodes, it still merges first, temporarily forming 4 nodes.

4. There are at most three nodes in the 2-3 tree, so the 4 nodes are split into a sub-tree, and the 4 nodes are transformed into a balanced tree composed of three 2 nodes. As shown in the figure, it can be understood as a binary search tree and a 2-3 tree, except that each node is two nodes, while the tree keeps absolute balance.
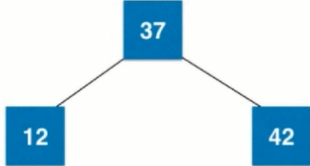
5. Add a new element 18 to the tree, the root node is 37. To add 18 to its left subtree 12, 18 > 12, add it to the right subtree of 12. At this time, the right subtree of 12 is empty. [The new node will never go empty, but will merge with the final leaf node] This tree remains absolute. Balance
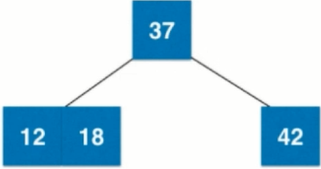
6. Adding a new element 6 to the tree, the root node is 37. To add 18 to its left subtree (including 3 nodes of 1218), 6 < 12 adds it to the left subtree of 3 nodes. At this time, the left subtree of 3 nodes is empty. So first merge into 4 nodes
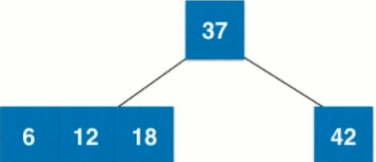
7. Disassemble 4 nodes into a subtree with 3 2 nodes
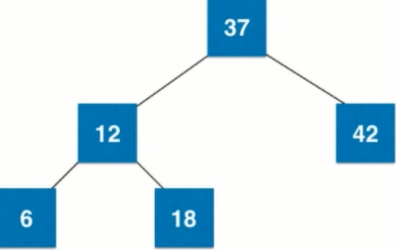
If the 2-3 tree is not absolutely balanced as shown in the figure above, for 2-3 tree, if the leaf node itself is already a 3-node, add a node to become 4 nodes, become as shown in the figure, then 12 needs to be fused with its parent node 37, 37 is 2 nodes, 12 and 37 can be fused directly. When three nodes are combined, the tree is still absolutely balanced
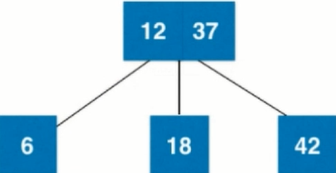
8. Adding a new element 11 to the tree, the root node is 3 nodes of 1237. To add 11 to its left subtree 6, 6 < 11, add it to the right subtree of 6. At this time, the right subtree of 6 is empty. node
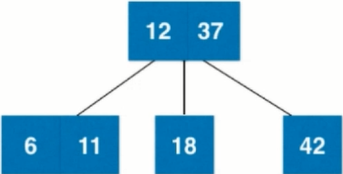
9. Adding a new element 5 to the tree, the root node is the 3 nodes of 1237. To add 5 to the 3 nodes of its left subtree 611, 5 < 6, so add it to the 3 nodes left subtree of 611. At this time, the left subtree of the 3 nodes of 611 is empty. [The new node will never go empty, but will only find the last leaves. Nodes do fusion, so the first fusion is 4 nodes.
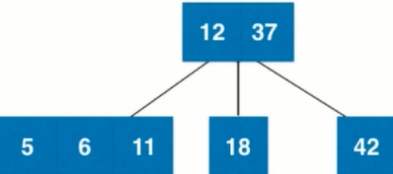
Decomposition of 4 nodes into a subtree with 3 2 nodes
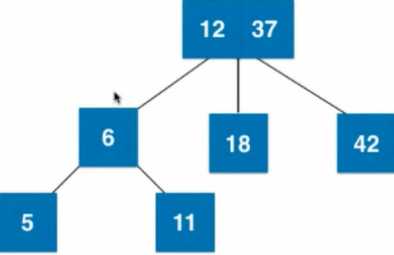
If the 2-3 tree is not absolutely balanced as shown in the figure above, for the 2-3 tree, if its leaf node itself is already a 3-node, add a node to become 4-node, become as shown in the figure, then 6 needs to merge with the 3-node of its parent node 1237 to become 4-node. Still absolutely balanced
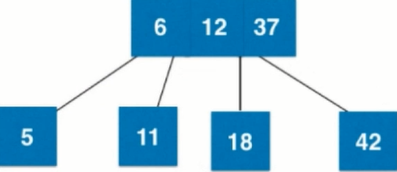
When 4 nodes are disassembled and transformed into a subtree containing 3 2 nodes, the tree is still absolutely balanced and keeps the properties of 2-3 trees.
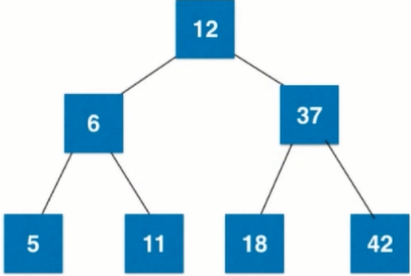
Summary:
If two nodes are inserted, three nodes are merged directly.

If three nodes are inserted, and they are root nodes, they are fused and then split.

If three nodes are inserted, the father node is two nodes. First, fusion, then split, and then fusion.

If three nodes are inserted, the father node is three nodes. First, fusion is followed by disassembly, and then fusion is followed by disassembly.
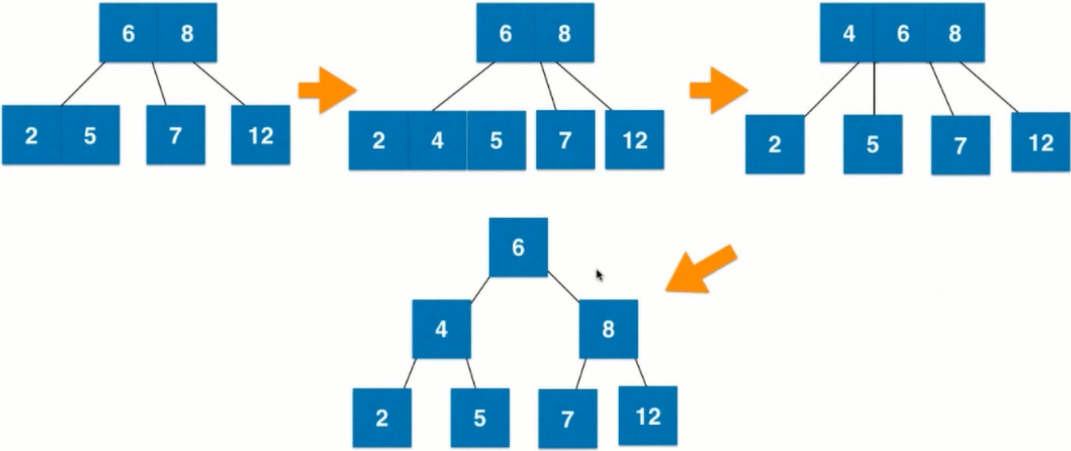
3. Equivalence of Red-Black Tree and 2-3 Tree
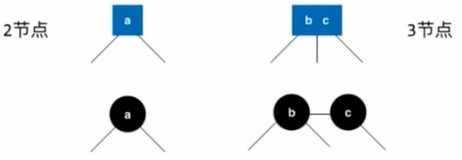
Represents that b and c are juxtaposed (stored together in 3 nodes), then sets their connections to red; restores them to the look of a binary search tree
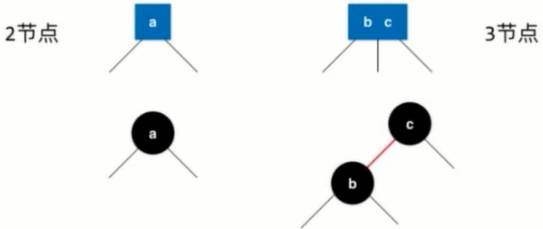
The method of expressing red connection: Because each node has only one father (each node has only one line at the edge of its father node), it can make a special mark to the b node to make it red, indicating that the b node and the c node are stored together in the 2-3 tree in three nodes [all the red nodes are left-leaning]. Oblique)
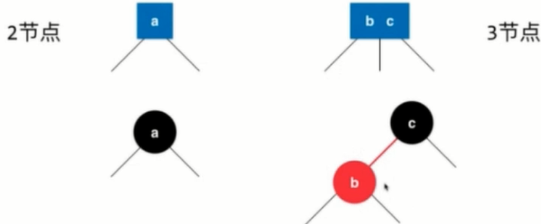
As shown in the figure.
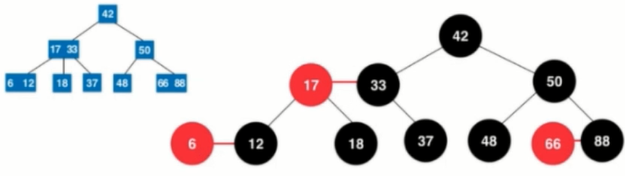
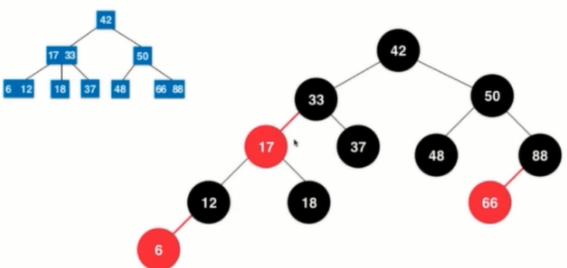
The nature of mangrove trees:
1. Each node is either red or black.
2. The root node is black.
3. Each leaf node (the last empty node) is black.
4. If a node is red, its two child nodes are black.
5. From any node to the leaf node (the last empty node), the number of black nodes passing through is the same [core]
Analysis: 2-3 trees are absolutely balanced, so all leaf nodes are on the same level, and their depths are the same; from any node, there is a fixed depth, from the node down to the (reachable) leaf nodes, the depth down is the same, the number of nodes it passes through is the same; corresponding to red and black. There are as many black nodes in the tree. [Red-black tree is a binary tree that keeps a "black balance". Its maximum height is 2log n and its time complexity is O(log n)]
Code implementation: RBTree.java
import java.util.ArrayList;
public class RBTree<K extends Comparable<K>, V> {
private static final boolean RED = true; //Define red as true
private static final boolean BLACK = false;//Define black as false
private class Node{
public K key;
public V value;
public Node left, right;
public boolean color; //Define node color
public Node(K key, V value){
this.key = key;
this.value = value;
left = null;
right = null;
color = RED; //Nodes are red by default.
}
}
private Node root;
private int size;
public RBTree(){
root = null;
size = 0;
}
public int getSize(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
// Judging the color of node
private boolean isRed(Node node){
if(node == null)
return BLACK;
return node.color;
}
// Add new elements (key, value) to the binary search tree
public void add(K key, V value){
root = add(root, key, value);
}
// A recursive algorithm for inserting elements (key, value) into a node-based binary search tree
// Returns the root of the binary search tree after inserting a new node
private Node add(Node node, K key, V value){
if(node == null){
size ++;
return new Node(key, value);
}
if(key.compareTo(node.key) < 0)
node.left = add(node.left, key, value);
else if(key.compareTo(node.key) > 0)
node.right = add(node.right, key, value);
else // key.compareTo(node.key) == 0
node.value = value;
return node;
}
// Returns the node where key is located in the binary search tree with node as its root node
private Node getNode(Node node, K key){
if(node == null)
return null;
if(key.equals(node.key))
return node;
else if(key.compareTo(node.key) < 0)
return getNode(node.left, key);
else // if(key.compareTo(node.key) > 0)
return getNode(node.right, key);
}
public boolean contains(K key){
return getNode(root, key) != null;
}
public V get(K key){
Node node = getNode(root, key);
return node == null ? null : node.value;
}
public void set(K key, V newValue){
Node node = getNode(root, key);
if(node == null)
throw new IllegalArgumentException(key + " doesn't exist!");
node.value = newValue;
}
// Returns the node where the minimum value of the binary search tree with node as its root is located
private Node minimum(Node node){
if(node.left == null)
return node;
return minimum(node.left);
}
// Delete the smallest node in the binary search tree with node as its root
// Returns the root of the new binary search tree after deleting the node
private Node removeMin(Node node){
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
// Delete key nodes from the binary search tree
public V remove(K key){
Node node = getNode(root, key);
if(node != null){
root = remove(root, key);
return node.value;
}
return null;
}
private Node remove(Node node, K key){
if( node == null )
return null;
if( key.compareTo(node.key) < 0 ){
node.left = remove(node.left , key);
return node;
}
else if(key.compareTo(node.key) > 0 ){
node.right = remove(node.right, key);
return node;
}
else{ // key.compareTo(node.key) == 0
// If the left subtree of the node to be deleted is empty
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
// The case where the right subtree of the node to be deleted is empty
if(node.right == null){
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
// The case that the left and right subtrees of the node to be deleted are not empty
// Find the smallest node larger than the node to be deleted, that is, the smallest node in the right subtree of the node to be deleted
// Use this node to replace the location of the node to be deleted
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}
public static void main(String[] args){
System.out.println("Pride and Prejudice");
ArrayList<String> words = new ArrayList<>();
if(FileOperation.readFile("pride-and-prejudice.txt", words)) {
System.out.println("Total words: " + words.size());
RBTree<String, Integer> map = new RBTree<>();
for (String word : words) {
if (map.contains(word))
map.set(word, map.get(word) + 1);
else
map.add(word, 1);
}
System.out.println("Total different words: " + map.getSize());
System.out.println("Frequency of PRIDE: " + map.get("pride"));
System.out.println("Frequency of PREJUDICE: " + map.get("prejudice"));
}
System.out.println();
}
}
IV. Adding Elements to Red-Black Trees and Left Rotation
Red and Black Tree Addition Elements:

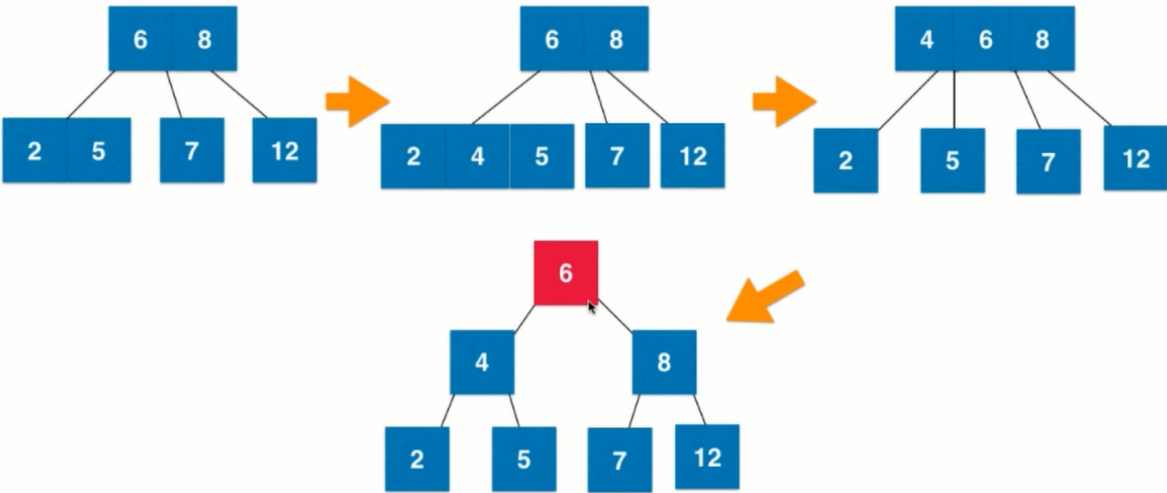
Keep the root node black
public void add(K key, V value){
root = add(root, key, value);
root.color = BLACK; // The final root node is a black node
}Add process: When the whole tree is empty, add 42 elements, make the root 42.

But in a red-black tree, the root node must be black, turning it black.

Insert element 37, insert to the location of the left child of 42, equivalent to 3 nodes in the 2-3 tree
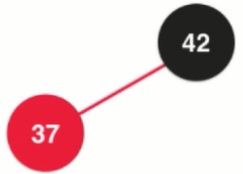
However, if the root node is 37 and the insertion element is 42, the definition of red-black tree is not satisfied (red node tilts left).
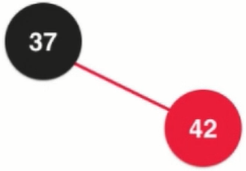
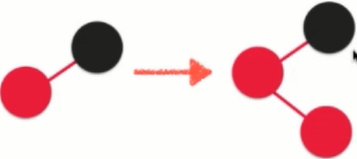
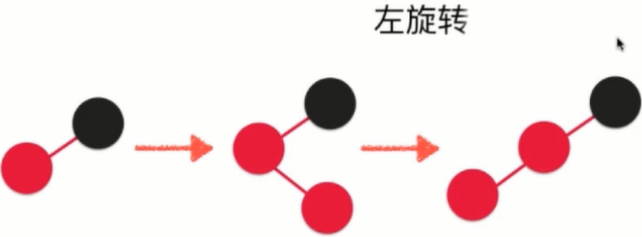
Solution: Turn left, the picture above turns left into the picture below.
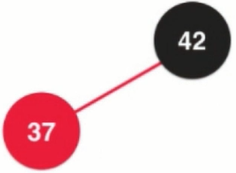
Left rotation process: 1. Suppose the root node is node and the right child of node is x.

2.node.right = x.left, let the right child of node be the left subtree of x, and still keep the property of binary search tree
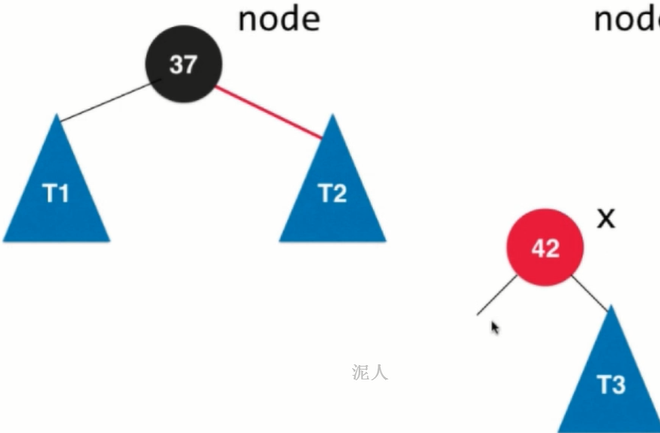
3.x.right = node. The left subtree of X connects the node and completes the left rotation. 37 turns from the father of 42 to the right child of 42, which is equivalent to counterclockwise rotation. In 37, it is left rotation.

4. For red-black trees, color information needs to be maintained.
x.color = node.color. The new root node is the x node. The color of the x node is the same as that of the previous node.
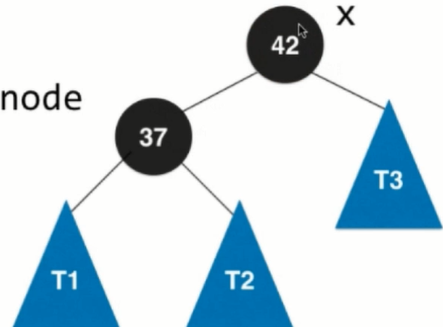
The left child whose node becomes x corresponds to the 4 temporary nodes in the 2-3 tree. To change the color of node into red, node.color = RED means that it is merged with its father node 42, thus completing the whole left rotation process.
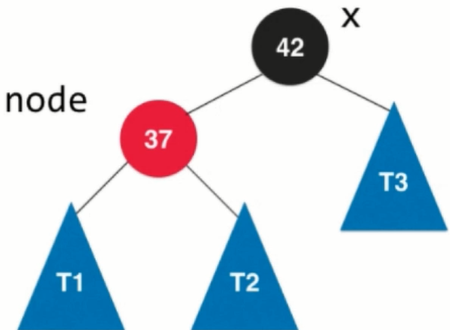
Code implementation: RBTree.java
import java.util.ArrayList;
public class RBTree<K extends Comparable<K>, V> {
private static final boolean RED = true;
private static final boolean BLACK = false;
private class Node{
public K key;
public V value;
public Node left, right;
public boolean color;
public Node(K key, V value){
this.key = key;
this.value = value;
left = null;
right = null;
color = RED;
}
}
private Node root;
private int size;
public RBTree(){
root = null;
size = 0;
}
public int getSize(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
// Judging the color of node
private boolean isRed(Node node){
if(node == null)
return BLACK;
return node.color;
}
// node x
// /\ Left rotation/\
// T1 x ---------> node T3
// / \ / \
// T2 T3 T1 T2
private Node leftRotate(Node node){
Node x = node.right;
// Left rotation [core]
node.right = x.left;
x.left = node;
x.color = node.color;
node.color = RED;
return x;
}
// Add new elements (key, value) to the red-black tree
public void add(K key, V value){
root = add(root, key, value);
root.color = BLACK; // The final root node is a black node
}
// Insert elements (key, value) into the red-black tree rooted by node, recursive algorithm
// Returns the root of the red-black tree after inserting a new node
private Node add(Node node, K key, V value){
if(node == null){
size ++;
return new Node(key, value); // Insert red nodes by default
}
if(key.compareTo(node.key) < 0)
node.left = add(node.left, key, value);
else if(key.compareTo(node.key) > 0)
node.right = add(node.right, key, value);
else // key.compareTo(node.key) == 0
node.value = value;
return node;
}
// Returns the node where key is located in the binary search tree with node as its root node
private Node getNode(Node node, K key){
if(node == null)
return null;
if(key.equals(node.key))
return node;
else if(key.compareTo(node.key) < 0)
return getNode(node.left, key);
else // if(key.compareTo(node.key) > 0)
return getNode(node.right, key);
}
public boolean contains(K key){
return getNode(root, key) != null;
}
public V get(K key){
Node node = getNode(root, key);
return node == null ? null : node.value;
}
public void set(K key, V newValue){
Node node = getNode(root, key);
if(node == null)
throw new IllegalArgumentException(key + " doesn't exist!");
node.value = newValue;
}
// Returns the node where the minimum value of the binary search tree with node as its root is located
private Node minimum(Node node){
if(node.left == null)
return node;
return minimum(node.left);
}
// Delete the smallest node in the binary search tree with node as its root
// Returns the root of the new binary search tree after deleting the node
private Node removeMin(Node node){
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
// Delete key nodes from the binary search tree
public V remove(K key){
Node node = getNode(root, key);
if(node != null){
root = remove(root, key);
return node.value;
}
return null;
}
private Node remove(Node node, K key){
if( node == null )
return null;
if( key.compareTo(node.key) < 0 ){
node.left = remove(node.left , key);
return node;
}
else if(key.compareTo(node.key) > 0 ){
node.right = remove(node.right, key);
return node;
}
else{ // key.compareTo(node.key) == 0
// If the left subtree of the node to be deleted is empty
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
// The case where the right subtree of the node to be deleted is empty
if(node.right == null){
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
// The case that the left and right subtrees of the node to be deleted are not empty
// Find the smallest node larger than the node to be deleted, that is, the smallest node in the right subtree of the node to be deleted
// Use this node to replace the location of the node to be deleted
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}
public static void main(String[] args){
System.out.println("Pride and Prejudice");
ArrayList<String> words = new ArrayList<>();
if(FileOperation.readFile("pride-and-prejudice.txt", words)) {
System.out.println("Total words: " + words.size());
RBTree<String, Integer> map = new RBTree<>();
for (String word : words) {
if (map.contains(word))
map.set(word, map.get(word) + 1);
else
map.add(word, 1);
}
System.out.println("Total different words: " + map.getSize());
System.out.println("Frequency of PRIDE: " + map.get("pride"));
System.out.println("Frequency of PREJUDICE: " + map.get("prejudice"));
}
System.out.println();
}
}
V. Color Flip and Right Rotation
Adding New Elements to Red and Black Trees
1. When the red-black tree itself is empty, add the node directly and keep it black.

2. Add a new node to the black node whose left and right subtrees are empty. If it is the left child of the black node, add it directly.
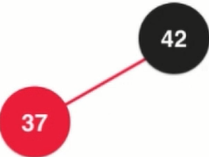
3. If you are the right child of a black node, you need to rotate left. [Put a new element into two nodes and convert two nodes into three operations in a red-black tree]
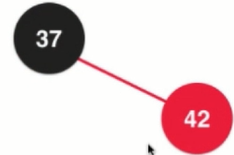
4. Adding elements to the three nodes of the red-black tree
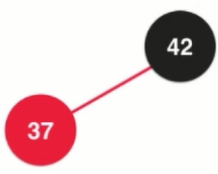
5. Add element 66, then [red: the node and its parent are fused together, 37 and 66 are red, are fused together, can be understood as temporary 4 nodes]
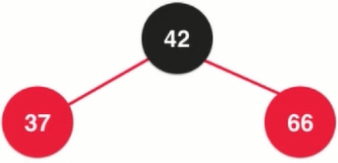
In the 2-3 tree, it is equivalent to the figure. Four nodes are divided into three and two nodes.

In the red-black tree, 4 nodes are divided into 3 2 nodes to represent 3 nodes which are all black. There is no red node on the left side of the black node, which represents a separate 2 nodes.
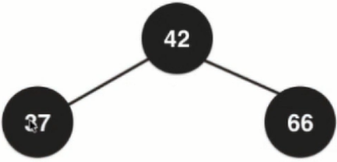
In the 2-3 tree, if 3 nodes are inserted, the father node is 2 nodes. First, fusion is done, then split, and then fusion is done.
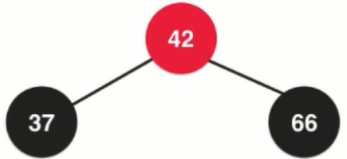
When the above elements are added, it is found that the color of the nodes in the red-black tree is just the opposite, which is called filpColors.
Add element 12 to the red-black tree below.
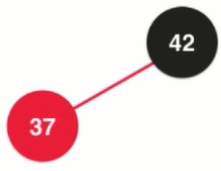
The rule of adding elements from the binary search tree knows that 12 is added to the left child of 37
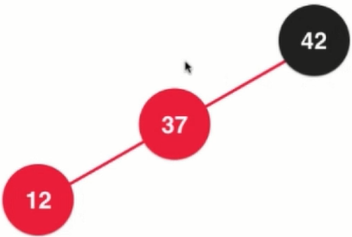
Equivalent to 2-3 trees, forming temporary 4 nodes

4 nodes to be split

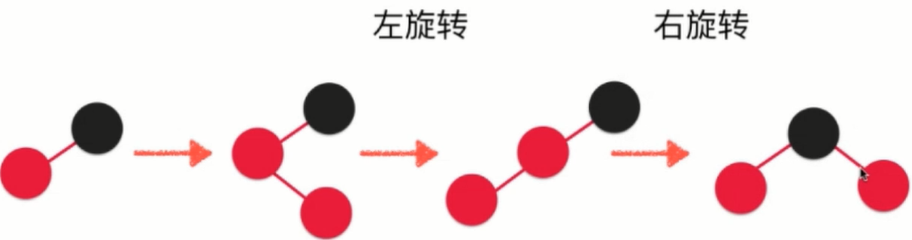
In red and black trees, right rotation is needed.
1. Suppose that the root node is node and the left child of node is x.

2.node.left = T1. Let the left subtree of node be the right subtree of the left child, and still keep the property of the binary search tree.
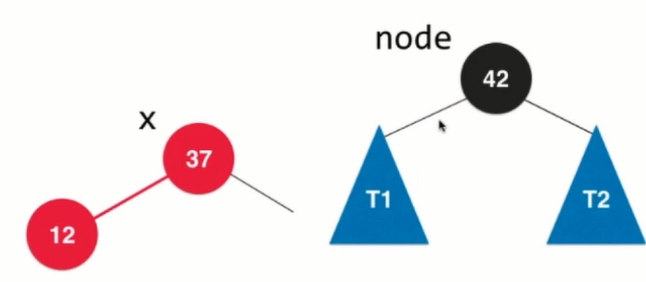
3.x.right = node, complete the right rotation, 42 from the original father of 37 to the right child of 37, equivalent to clockwise rotation, in 37 to see the right rotation.
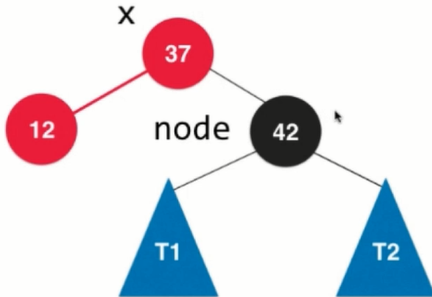
4. For red-black trees, color information needs to be maintained.
x.color = node.color. The new root node is the x node. The color of the x node is the same as that of the previous node.
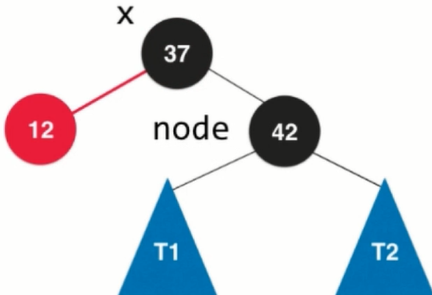
The right child whose node becomes x corresponds to the 4 temporary nodes in the 2-3 tree. To change the color of node into red, node.color = RED indicates that it is merged with its father node 42, thus completing the whole right rotation process.

Code implementation: color flip
RBTree.java
import java.util.ArrayList;
public class RBTree<K extends Comparable<K>, V> {
private static final boolean RED = true;
private static final boolean BLACK = false;
private class Node{
public K key;
public V value;
public Node left, right;
public boolean color;
public Node(K key, V value){
this.key = key;
this.value = value;
left = null;
right = null;
color = RED;
}
}
private Node root;
private int size;
public RBTree(){
root = null;
size = 0;
}
public int getSize(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
// Judging the color of node
private boolean isRed(Node node){
if(node == null)
return BLACK;
return node.color;
}
// node x
// /\ Left rotation/\
// T1 x ---------> node T3
// / \ / \
// T2 T3 T1 T2
private Node leftRotate(Node node){
Node x = node.right;
// Left rotation
node.right = x.left;
x.left = node;
x.color = node.color;
node.color = RED;
return x;
}
// node x
// /\ Right rotation/\
// x T2 -------> y node
// / \ / \
// y T1 T1 T2
private Node rightRotate(Node node){
Node x = node.left;
// Right rotation
node.left = x.right;
x.right = node;
x.color = node.color;
node.color = RED;
return x;
}
// Color reversal
private void flipColors(Node node){
node.color = RED;
node.left.color = BLACK;
node.right.color = BLACK;
}
// Add new elements (key, value) to the red-black tree
public void add(K key, V value){
root = add(root, key, value);
root.color = BLACK; // The final root node is a black node
}
// Insert elements (key, value) into the red-black tree rooted by node, recursive algorithm
// Returns the root of the red-black tree after inserting a new node
private Node add(Node node, K key, V value){
if(node == null){
size ++;
return new Node(key, value); // Insert red nodes by default
}
if(key.compareTo(node.key) < 0)
node.left = add(node.left, key, value);
else if(key.compareTo(node.key) > 0)
node.right = add(node.right, key, value);
else // key.compareTo(node.key) == 0
node.value = value;
return node;
}
// Returns the node where key is located in the binary search tree with node as its root node
private Node getNode(Node node, K key){
if(node == null)
return null;
if(key.equals(node.key))
return node;
else if(key.compareTo(node.key) < 0)
return getNode(node.left, key);
else // if(key.compareTo(node.key) > 0)
return getNode(node.right, key);
}
public boolean contains(K key){
return getNode(root, key) != null;
}
public V get(K key){
Node node = getNode(root, key);
return node == null ? null : node.value;
}
public void set(K key, V newValue){
Node node = getNode(root, key);
if(node == null)
throw new IllegalArgumentException(key + " doesn't exist!");
node.value = newValue;
}
// Returns the node where the minimum value of the binary search tree with node as its root is located
private Node minimum(Node node){
if(node.left == null)
return node;
return minimum(node.left);
}
// Delete the smallest node in the binary search tree with node as its root
// Returns the root of the new binary search tree after deleting the node
private Node removeMin(Node node){
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
// Delete key nodes from the binary search tree
public V remove(K key){
Node node = getNode(root, key);
if(node != null){
root = remove(root, key);
return node.value;
}
return null;
}
private Node remove(Node node, K key){
if( node == null )
return null;
if( key.compareTo(node.key) < 0 ){
node.left = remove(node.left , key);
return node;
}
else if(key.compareTo(node.key) > 0 ){
node.right = remove(node.right, key);
return node;
}
else{ // key.compareTo(node.key) == 0
// If the left subtree of the node to be deleted is empty
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
// The case where the right subtree of the node to be deleted is empty
if(node.right == null){
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
// The case that the left and right subtrees of the node to be deleted are not empty
// Find the smallest node larger than the node to be deleted, that is, the smallest node in the right subtree of the node to be deleted
// Use this node to replace the location of the node to be deleted
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}
public static void main(String[] args){
System.out.println("Pride and Prejudice");
ArrayList<String> words = new ArrayList<>();
if(FileOperation.readFile("pride-and-prejudice.txt", words)) {
System.out.println("Total words: " + words.size());
RBTree<String, Integer> map = new RBTree<>();
for (String word : words) {
if (map.contains(word))
map.set(word, map.get(word) + 1);
else
map.add(word, 1);
}
System.out.println("Total different words: " + map.getSize());
System.out.println("Frequency of PRIDE: " + map.get("pride"));
System.out.println("Frequency of PREJUDICE: " + map.get("prejudice"));
}
System.out.println();
}
}
Summary:
1.
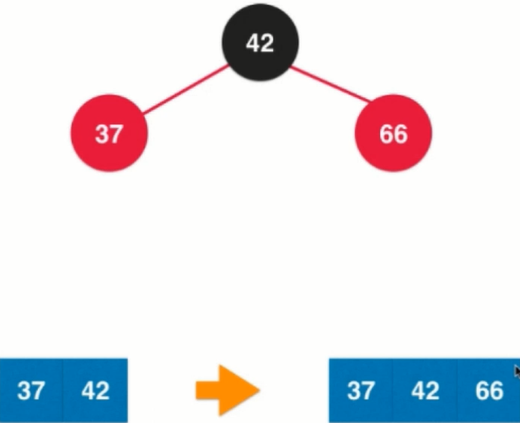
2.
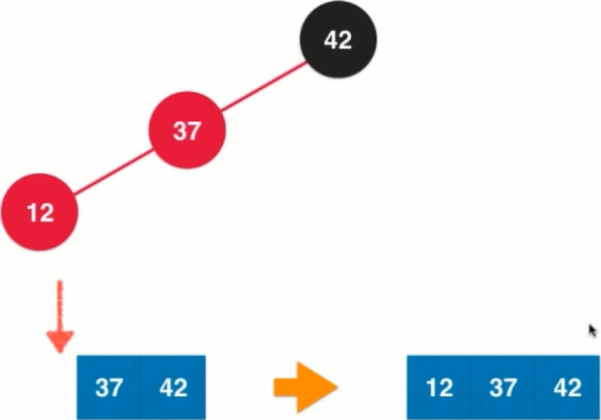
3.
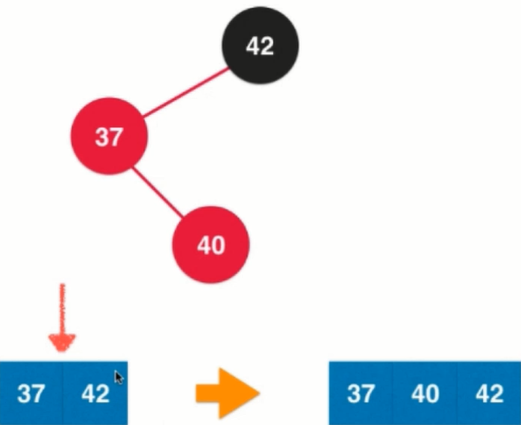
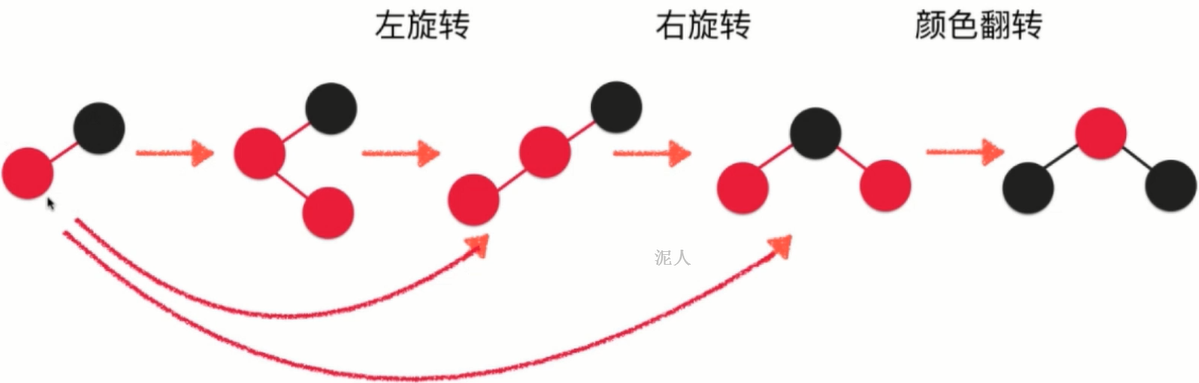
This solution: 1. Left rotation
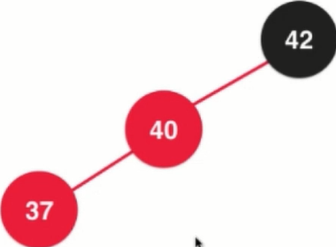
2. Rotate right again
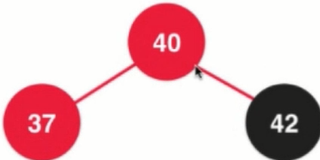
3. Maintaining color
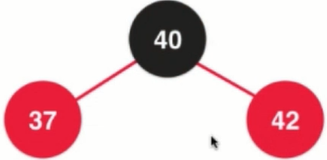
4. Color reversal
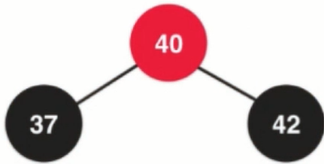
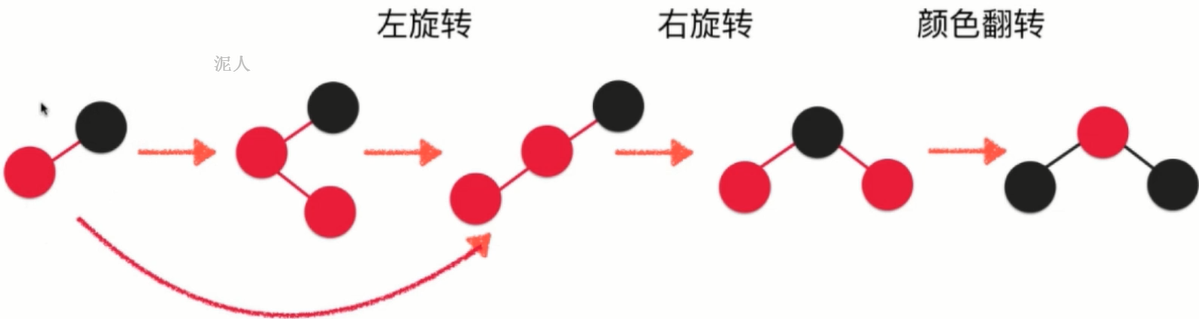
The most complex addition element: the new addition node is in the middle of the corresponding 2-3 tree
Rotate left on two red nodes
Right rotation for black nodes
Color reversal

Adding elements smaller than these two elements to the three nodes equivalent to the 2-3 tree,
If an element larger than the maximum value of the two elements [black] is added to the three nodes equivalent to the 2-3 tree, then
Maintenance timing: Like AVL trees, add nodes and backtrack upward maintenance
Red and Black Tree [Final Edition] Code: RBTree.java
import java.util.ArrayList;
public class RBTree<K extends Comparable<K>, V> {
private static final boolean RED = true;
private static final boolean BLACK = false;
private class Node{
public K key;
public V value;
public Node left, right;
public boolean color;
public Node(K key, V value){
this.key = key;
this.value = value;
left = null;
right = null;
color = RED;
}
}
private Node root;
private int size;
public RBTree(){
root = null;
size = 0;
}
public int getSize(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
// Judging the color of node
private boolean isRed(Node node){
if(node == null)
return BLACK;
return node.color;
}
// node x
// /\ Left rotation/\
// T1 x ---------> node T3
// / \ / \
// T2 T3 T1 T2
private Node leftRotate(Node node){
Node x = node.right;
// Left rotation
node.right = x.left;
x.left = node;
x.color = node.color;
node.color = RED;
return x;
}
// node x
// /\ Right rotation/\
// x T2 -------> y node
// / \ / \
// y T1 T1 T2
private Node rightRotate(Node node){
Node x = node.left;
// Right rotation
node.left = x.right;
x.right = node;
x.color = node.color;
node.color = RED;
return x;
}
// Color reversal
private void flipColors(Node node){
node.color = RED;
node.left.color = BLACK;
node.right.color = BLACK;
}
// Add new elements (key, value) to the red-black tree
public void add(K key, V value){
root = add(root, key, value);
root.color = BLACK; // The final root node is a black node
}
// Insert elements (key, value) into the red-black tree rooted by node, recursive algorithm
// Returns the root of the red-black tree after inserting a new node
private Node add(Node node, K key, V value){
if(node == null){
size ++;
return new Node(key, value); // Insert red nodes by default
}
if(key.compareTo(node.key) < 0)
node.left = add(node.left, key, value);
else if(key.compareTo(node.key) > 0)
node.right = add(node.right, key, value);
else // key.compareTo(node.key) == 0
node.value = value;
if (isRed(node.right) && !isRed(node.left))
node = leftRotate(node);
if (isRed(node.left) && isRed(node.left.left))
node = rightRotate(node);
if (isRed(node.left) && isRed(node.right))
flipColors(node);
return node;
}
// Returns the node where key is located in the binary search tree with node as its root node
private Node getNode(Node node, K key){
if(node == null)
return null;
if(key.equals(node.key))
return node;
else if(key.compareTo(node.key) < 0)
return getNode(node.left, key);
else // if(key.compareTo(node.key) > 0)
return getNode(node.right, key);
}
public boolean contains(K key){
return getNode(root, key) != null;
}
public V get(K key){
Node node = getNode(root, key);
return node == null ? null : node.value;
}
public void set(K key, V newValue){
Node node = getNode(root, key);
if(node == null)
throw new IllegalArgumentException(key + " doesn't exist!");
node.value = newValue;
}
// Returns the node where the minimum value of the binary search tree with node as its root is located
private Node minimum(Node node){
if(node.left == null)
return node;
return minimum(node.left);
}
// Delete the smallest node in the binary search tree with node as its root
// Returns the root of the new binary search tree after deleting the node
private Node removeMin(Node node){
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
// Delete key nodes from the binary search tree
public V remove(K key){
Node node = getNode(root, key);
if(node != null){
root = remove(root, key);
return node.value;
}
return null;
}
private Node remove(Node node, K key){
if( node == null )
return null;
if( key.compareTo(node.key) < 0 ){
node.left = remove(node.left , key);
return node;
}
else if(key.compareTo(node.key) > 0 ){
node.right = remove(node.right, key);
return node;
}
else{ // key.compareTo(node.key) == 0
// If the left subtree of the node to be deleted is empty
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
// The case where the right subtree of the node to be deleted is empty
if(node.right == null){
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
// The case that the left and right subtrees of the node to be deleted are not empty
// Find the smallest node larger than the node to be deleted, that is, the smallest node in the right subtree of the node to be deleted
// Use this node to replace the location of the node to be deleted
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}
public static void main(String[] args){
System.out.println("Pride and Prejudice");
ArrayList<String> words = new ArrayList<>();
if(FileOperation.readFile("pride-and-prejudice.txt", words)) {
System.out.println("Total words: " + words.size());
RBTree<String, Integer> map = new RBTree<>();
for (String word : words) {
if (map.contains(word))
map.set(word, map.get(word) + 1);
else
map.add(word, 1);
}
System.out.println("Total different words: " + map.getSize());
System.out.println("Frequency of PRIDE: " + map.get("pride"));
System.out.println("Frequency of PREJUDICE: " + map.get("prejudice"));
}
System.out.println();
}
}
Output:

6. Performance Testing of Red-Black Trees
Main.java
import java.util.ArrayList;
public class Main {
public static void main(String[] args) {
System.out.println("Pride and Prejudice");
ArrayList<String> words = new ArrayList<>();
if(FileOperation.readFile("pride-and-prejudice.txt", words)) {
System.out.println("Total words: " + words.size());
// Collections.sort(words);
// Test BST
long startTime = System.nanoTime();
BST<String, Integer> bst = new BST<>();
for (String word : words) {
if (bst.contains(word))
bst.set(word, bst.get(word) + 1);
else
bst.add(word, 1);
}
for(String word: words)
bst.contains(word);
long endTime = System.nanoTime();
double time = (endTime - startTime) / 1000000000.0;
System.out.println("BST: " + time + " s");
// Test AVL
startTime = System.nanoTime();
AVLTree<String, Integer> avl = new AVLTree<>();
for (String word : words) {
if (avl.contains(word))
avl.set(word, avl.get(word) + 1);
else
avl.add(word, 1);
}
for(String word: words)
avl.contains(word);
endTime = System.nanoTime();
time = (endTime - startTime) / 1000000000.0;
System.out.println("AVL: " + time + " s");
// Test RBTree
startTime = System.nanoTime();
RBTree<String, Integer> rbt = new RBTree<>();
for (String word : words) {
if (rbt.contains(word))
rbt.set(word, rbt.get(word) + 1);
else
rbt.add(word, 1);
}
for(String word: words)
rbt.contains(word);
endTime = System.nanoTime();
time = (endTime - startTime) / 1000000000.0;
System.out.println("RBTree: " + time + " s");
}
System.out.println();
}
}
Output: Red-black tree performance is not superior: most operations in the query, red-black tree is good at adding / deleting [relative to AVL tree];

Test only add operations: Main2.java
import java.util.ArrayList;
import java.util.Random;
public class Main2 {
public static void main(String[] args) {
// int n = 20000000;
int n = 20000000;
Random random = new Random(n);
ArrayList<Integer> testData = new ArrayList<>(n);
for(int i = 0 ; i < n ; i ++)
testData.add(random.nextInt(Integer.MAX_VALUE));
// Test BST
long startTime = System.nanoTime();
BST<Integer, Integer> bst = new BST<>();
for (Integer x: testData)
bst.add(x, null);
long endTime = System.nanoTime();
double time = (endTime - startTime) / 1000000000.0;
System.out.println("BST: " + time + " s");
// Test AVL
startTime = System.nanoTime();
AVLTree<Integer, Integer> avl = new AVLTree<>();
for (Integer x: testData)
avl.add(x, null);
endTime = System.nanoTime();
time = (endTime - startTime) / 1000000000.0;
System.out.println("AVL: " + time + " s");
// Test RBTree
startTime = System.nanoTime();
RBTree<Integer, Integer> rbt = new RBTree<>();
for (Integer x: testData)
rbt.add(x, null);
endTime = System.nanoTime();
time = (endTime - startTime) / 1000000000.0;
System.out.println("RBTree: " + time + " s");
}
}
Output: [Random] Red-black trees have an advantage over AVL in addition/deletion operations

Summary of performance of mangrove trees:
