This question should be the most laborious one recently brushed, but I also learned a lot of new data structures and ideas.

There are three operations in this problem: adding an element to the data structure, removing the element with the largest weight, and removing the element with the smallest weight.

Of course, you can use arrays to insert an element using binary search when adding, but it takes a lot of time.

Since only the elements with the largest and smallest weight are needed each time, this is very similar to the heap, and it is very easy to insert an element into the heap.

But the heap can only take the largest heap and the smallest heap. You can't create two heaps at the same time, can you?

After searching relevant information on the Internet, I learned a data structure called heap, which is a combined version of heap and tree. The tree here is a binary search tree.

The essence of heap is that data is obtained by binary balanced tree and random numbers are used to maintain the heap.

Before understanding the tree, let's first take a look at the binary search tree and heap: (those familiar with these two data structures can skip this paragraph)

Heap: the priority queue we often use is actually based on heap. There are two types of heap: maximum heap and minimum heap. Here, take the minimum heap as an example to introduce the properties of heap. Heap is actually a kind of binary tree.

Minimum heap: in the minimum heap, the value of each child node is not greater than the value of its parent node. As for heap, first of all, it has two basic operations, and other derivative operations are carried out on the basis of these two basic operations. These two operations are to move an element in the heap to a suitable position to the top, and to move an element in the heap to a suitable position to the bottom. On the basis of these two, there are two basic ideas: path compression and rank merging, which are used to maintain heap balance. From these operations, algorithms such as inserting an element, deleting an element, heap sorting, and converting an array into heap are derived. The detailed implementation process is not introduced here. Please search "implementation of heap".

About binary search tree: for any node in the binary search tree, if it has a left subtree, the value of the node is greater than that of any node on its left subtree. If it has a right subtree, the value of the node is smaller than that of any node on its right subtree. The specific implementation can search "the nature and implementation of binary search tree".

Tree is very similar to binary search tree. It obtains the most value by finding the leftmost and rightmost nodes. The difference is that it uses heap method to maintain the tree.
Each node of the tree will be given a random value by generating a random number, and the random value will be used to maintain the balance of the binary tree.

To sum up, we use random numbers to maintain this tree, but the way to find the most value is consistent with BST. Therefore, the key point is to add, delete and maintain. First introduce the operation of maintaining this tree: rotation, and then introduce the operation of adding and deleting nodes. Rotation: rotation is divided into left rotation and right rotation, which respectively represent two maintenance operations.

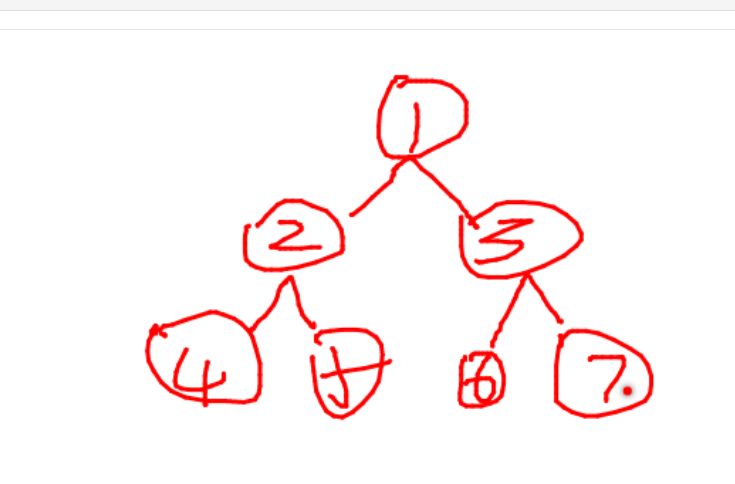
This is a binary tree. After left rotation, take the right child of the root node as the new root node, the original root node as the left child of the new root node, and the left child of the new root node as the right child of the old root node. It looks like it is equivalent to rotating to the left, and then give the extra child of the new root node No. 3 to the old root node No. 1 who has lost a child. As shown below:

Right rotation is the same. There is no drawing here. You can find other information.
Insert: it is the same as BST's insert operation, except that after insertion, its priority and its child's priority should be compared to determine whether to rotate (because the insert is compared with the root node first and then gradually to the lower level, it is not necessary to compare its priority with its parent node.)
Delete: deletion is complicated. First, if there are multiple elements on the deleted node, you only need to reduce its number by one. If there is one and there is no child node, you can delete it directly; If the deleted node has no right child node, or the priority of the left child node is higher than the right child node, the subtree with the deleted element as the root will rotate to the right. (make the left child become the root element of the subtree with the delete element as the root). At this time, only the new right child node needs to be deleted. Otherwise, the subtree with the deleted element as the root will rotate left and continue to delete the new left child node.

The specific implementation code is not written here. Please directly look at the bottom code.

#include<iostream>
#include<algorithm>
#include<stdlib.h>
using namespace std;
/*
* This topic should adopt the data structure of treap
* treap The essence of is that the data is obtained by binary balanced tree and random numbers are used to maintain the heap
* However, because the direct use of binary linked list will lead to timeout, the data structure is changed to use index array
*/
#define MAX 500010
struct Node {
	int K;
	int P;
	int random;
	int left, right;	//Use the value of 0 to determine whether it is a leaf node
	int size;
	int countK;
} nodes[MAX];
int index = 0;
int root;

int getNewNode(int k, int p) {
	nodes[++index].K = k;
	nodes[index].P = p;
	nodes[index].random = rand();
	nodes[index].countK = nodes[index].size = 1;
	return index;
}
void addSize(int no) {
	nodes[no].size = nodes[nodes[no].left].size + nodes[nodes[no].right].size + nodes[no].countK;
}
void init() {
	getNewNode(0 ,-0x3f3f3f3f);	//1
	getNewNode(0, 0x3f3f3f3f);	//2
	root = 1;
	nodes[1].right = 2;
	addSize(1);					//1 is the parent node
}
void rotateRight(int &node) {
	int temp = nodes[node].left;
	nodes[node].left = nodes[temp].right;
	nodes[temp].right = node;
	node = temp;
	//size must be calculated from bottom to top, otherwise an error will occur
	addSize(nodes[node].right);
	addSize(node);
}
void rotateLeft(int& node) {
	int temp = nodes[node].right;
	nodes[node].right = nodes[temp].left;
	nodes[temp].left = node;
	node = temp;
	addSize(nodes[node].left);
	addSize(node);
}
void insert(int& node, int k, int p) {
	if (!node) {
		node = getNewNode(k, p);
		return;
	}
	if (nodes[node].P == p)nodes[node].countK++;
	else if (p < nodes[node].P) {
		insert(nodes[node].left, k, p);
		if (nodes[nodes[node].left].random > nodes[node].random) rotateRight(node);
	}
	else
	{
		insert(nodes[node].right, k, p);
		if (nodes[nodes[node].right].random > nodes[node].random) rotateLeft(node);
	}
	addSize(node);	//Recalculate the size value of node
}
void remove(int& node, int p) {
	if (!node) return;
	if (nodes[node].P == p) {
		if (nodes[node].countK > 1) nodes[node].countK--;
		else if (nodes[node].left == 0 && nodes[node].right == 0) {
			node = 0;
		}
		else
		{
			if (nodes[node].left == 0 || nodes[nodes[node].right].random > nodes[nodes[node].left].random) {
				rotateLeft(node);
				remove(nodes[node].left, p);	//The original node is on the left branch
			}
			else
			{
				rotateRight(node);
				remove(nodes[node].right, p);	//After right rotation, the original node is on the right branch
			}
		}
	}
	else if (nodes[node].P > p) remove(nodes[node].left, p);
	else remove(nodes[node].right, p);
	addSize(node);
}
int getPbyPos(int node, int pos) {
	if (!node) return 0x3f3f3f3f;
	if (nodes[nodes[node].left].size >= pos) return getPbyPos(nodes[node].left, pos);
	else if (nodes[nodes[node].left].size + nodes[node].countK >= pos) {
		cout << nodes[node].K << endl;
		return nodes[node].P;
	}
	else return getPbyPos(nodes[node].right, pos - nodes[nodes[node].left].size - nodes[node].countK);
}

int main() {
	index = 0;
	init();
	int op;
	int totalNum = 2;
	int k, p;
	while (cin >> op,op) {
	if (op == 1) {
			cin >> k >> p;
			insert(root, k, p);
			totalNum++;
		}
		else if (op == 2) {
			if (totalNum == 2)cout << 0 << endl;
			else
			{
				p = getPbyPos(root, totalNum-1);
				remove(root, p);
				totalNum--;
			}
		}
		else
		{
			if (totalNum == 2)cout << 0 << endl;
			else
			{
				p = getPbyPos(root, 2);
				remove(root, p);
				totalNum--;
			}
		}
	}
	return 0;
}