Title Description

Enter an integer array to determine whether the array is the result of a post-order traversal of a binary search tree. If yes, output Yes, otherwise output No. Assume that any two numbers of the input array are different from each other.

Knowledge points:

1. Post-order traversal is "left and right roots".

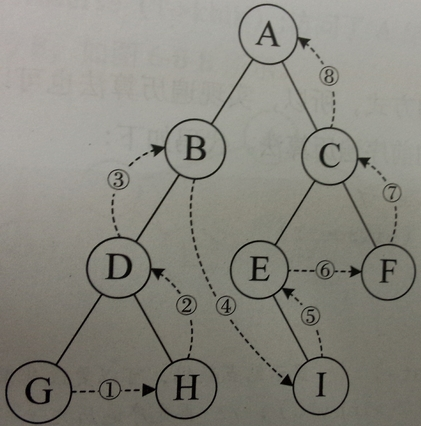
So the last element in the array traverses to the root node, so the last element in the array is the root node.

2. Characteristic of binary search tree: Nodes in left subtree are smaller than root node, and nodes in right subtree are larger than root node.

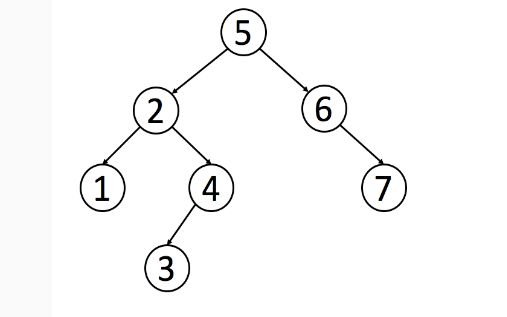
The array obtained by this post-order traversal is {1,3,4,2,7,6,5};

It can be judged from the array that the front part is left subtree smaller than root, and the back part is right subtree. If there is a number smaller than root in the right subtree, it does not conform to the characteristics of binary search tree. The number 1,3,4,2 is less than 5, which is located on the left subtree, and 7,6 is greater than 5, which is located on the right subtree.

Note that from the first number larger than the root node, the latter elements belong to the right subtree. If the number of sub-trees on the right side is larger than the number of root nodes, this is not a binary search tree.

For example, the root node of the array {7,4,6,5} is 5. According to the traversal order of the left and right roots and the characteristics of the binary tree, 7 is larger than 5. Then 7 should belong to the right subtree, and 7,4,6 are all the right subtrees.

Conventional solution:

class Solution {
public:
    bool VerifySquenceOfBST(vector<int> sequence) {
        return bst(sequence,0,sequence.size()-1);
    }
    bool bst(vector<int>sequence,int begin,int end)
    {
        if(sequence.empty()||begin>end)
            return false;
        // The last number of post-sequential traversals is the root node
        int root=sequence[end];
        //  Arrays are divided into left and right subtrees according to the root node
        int i=begin;
        for(;i<end;i++)
        {
            if(sequence[i]>root)  //At this point i is the first node belonging to the right subtree
                break;
        }
        //The number on the right is smaller than the root node, which is not a binary search tree.
        for(int j=i;j<end;j++)
        {
            if(sequence[j]<root)
                return false;
        }
        bool left=true;
        if(i>begin)  //Left subtree exists
            left=bst(sequence,begin,i-1);
        bool right=true;
        if(i<end-1)//The right subtree exists. end is the current root node. end-1 is the next root node.
            right=bst(sequence,i,end-1);
        return left&&right;
    }
};

There is another solution:

class Solution {
public:
    bool VerifySquenceOfBST(vector<int> sequence) {
        if(sequence.empty())
            return false;
        int len=sequence.size();
        int i=0;
        while(len)
        {
            int root=sequence[len-1];  //Root node
            //Counting the first part of the data smaller than root until the number larger than root stops, i.e. encountering the right subtree node
            while(sequence[i]<root)
                i++;  
            //The latter part of the count is larger than root. If there is a smaller number than root, the i count stops.
            while(sequence[i]>root)
                i++;   
            if(i<len-1) //It shows that the part after unsatisfactory is greater than root.
                return false;
            i=0;  //Note that the value of i is updated every time, and each iteration starts from scratch.
            len--;  //
        }
        return true;
    }
};