Binary sort tree
Requirements: for a sequence (7, 3, 10, 12, 5, 1, 9), it is required to query and add data efficiently
Basic introduction:
Binary sort tree: BST: (Binary Sort(Search) Tree). For any non leaf node of the binary sort tree, the value of the left child node is required to be smaller than that of the current node, and the value of the right child node is required to be larger than that of the current node.
Special note: if you have the same value, you can put this node on the left child node or the right child node
For example, for the previous data (7, 3, 10, 12, 5, 1, 9), the corresponding binary sort tree is:
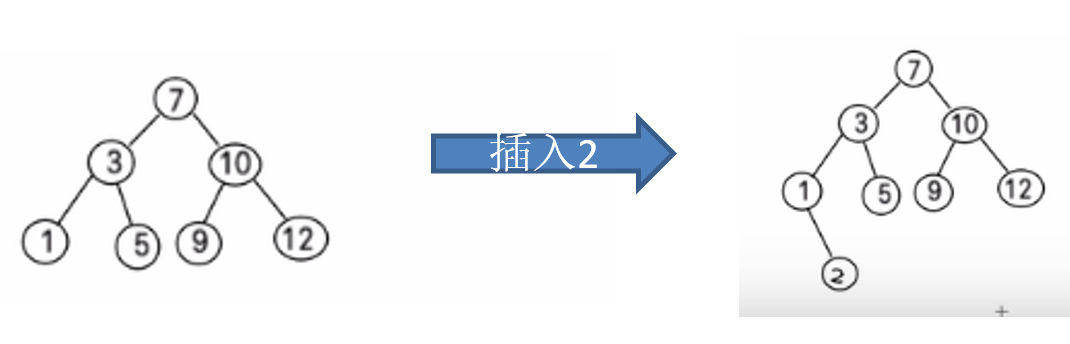
Binary sort tree creation and traversal
An array is created into the corresponding binary sort tree, and the middle order is used to traverse the binary sort tree
package com.atguigu.binarysorttree;
/**
* @ClassName BinarySortTreeDemo
* @Author Jeri
* @Date 2022-02-26 17:58
* @Description Creation, traversal and deletion of binary sort tree
*/
//Create node class object
class Node{
int value;
Node left;
Node right;
public Node(int value){
this.value = value;
}
//Override toString method
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
//Middle order traversal
public void infixOrder(){
if(this.left != null){
this.left.infixOrder();
}
System.out.println(this);
if(this.right != null){
this.right.infixOrder();
}
}
//Add node
public void add(Node node){
//Handling special situations
if(node == null){ return; }
//Judge node Value and this Value size relationship
if(this.value > node.value){
//Look left
if(this.left == null){
this.left = node;
}else{
this.left.add(node);
}
}else{
//Look right
if(this.right == null){
this.right = node;
}else{
this.right.add(node);
}
}
}
}
//Create a binary sort tree management node
class BinarySortTree{
private Node root;
public Node getRoot() {
return root;
}
public void setRoot(Node root) {
this.root = root;
}
//Add node to binary tree
public void add(Node node){
if(root == null){
this.root = node;
}else{
this.root.add(node);
}
}
//Order traversal in binary tree
public void infixOrder(){
if(this.root != null){
this.root.infixOrder();
}else{
System.out.println("Empty tree cannot be traversed");
}
}
}
public class BinarySortTreeDemo {
public static void main(String[] args) {
int[] array = new int[]{7, 3, 10, 12, 5, 1, 9};
//Create a binary tree object
BinarySortTree bst = new BinarySortTree();
//Add node object
for(Integer temp:array){
bst.add(new Node(temp));
}
//Middle order traversal
System.out.println("Middle order traversal:----");
bst.infixOrder();
}
}
Middle order traversal:----
Node{value=1}
Node{value=3}
Node{value=5}
Node{value=7}
Node{value=9}
Node{value=10}
Node{value=12}
Binary sort tree deletion
The deletion of binary sort tree is complex. There are three situations to consider:
- Delete leaf node
- Delete a node with only one subtree
- Delete a node with two subtrees
Train of thought analysis:
Delete leaf node
- You need to find the targetNode of the node to be deleted first
- Find the parent node of targetNode
- Determine whether the targetNode is the left child node or the right child node of the parent
- Delete according to the previous situation
Delete a node with only one subtree
- You need to find the targetNode of the node to be deleted first
- Find the parent node of targetNode
- Determines whether the child node of the targetNode is a left child node or a right child node
- Determines whether the child node of the targetNode is a left child node or a right child node
- Delete according to the previous situation
Delete a node with two subtrees
- You need to find the targetNode of the node to be deleted first
- Find the parent node of targetNode
- Find the smallest node from the right subtree of targetNode
- Use a temporary variable to save the value of the smallest node to temp
- Delete the minimum node
- Assign the value of temp to targetNode
package com.atguigu.binarysorttree;
/**
* @ClassName BinarySortTreeDemo
* @Author Jeri
* @Date 2022-02-26 17:58
* @Description Creation, traversal and deletion of binary sort tree
*/
//Create node class object
class Node{
int value;
Node left;
Node right;
public Node(int value){
this.value = value;
}
//Override toString method
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
//Middle order traversal
public void infixOrder(){
if(this.left != null){
this.left.infixOrder();
}
System.out.println(this);
if(this.right != null){
this.right.infixOrder();
}
}
//Add node
public void add(Node node){
//Handling special situations
if(node == null){ return; }
//Judge node Value and this Value size relationship
if(this.value > node.value){
//Look left
if(this.left == null){
this.left = node;
}else{
this.left.add(node);
}
}else{
//Look right
if(this.right == null){
this.right = node;
}else{
this.right.add(node);
}
}
}
//Find the node to be deleted
public Node search(int value){
if(this.value == value){
return this;
}else if(this.value > value){
//Left recursive search
if(this.left == null){
return null;
}
return this.left.search(value);
}else{
//Recursive right
if(this.right == null){
return null;
}
return this.right.search(value);
}
}
//Find the parent node of the node to be deleted
public Node searchParent(int value){
//Judge the current node
if((this.left != null && this.left.value == value) ||
(this.right != null && this.right.value == value)){
return this;
}else{
//The left child node of the current node is not empty and the value is greater than the lookup value
if(this.left != null && this.value > value){
return this.left.searchParent(value);
}else if(this.right != null && this.value < value){
//The right child node of the current node is not empty and the value is less than the lookup value
return this.right.searchParent(value);
}else{
//Parent node not found
return null;
}
}
}
}
//Create a binary sort tree management node
class BinarySortTree{
private Node root;
public Node getRoot() {
return root;
}
public void setRoot(Node root) {
this.root = root;
}
//Add node to binary tree
public void add(Node node){
if(root == null){
this.root = node;
}else{
this.root.add(node);
}
}
//Order traversal in binary tree
public void infixOrder(){
if(this.root != null){
this.root.infixOrder();
}else{
System.out.println("Empty tree cannot be traversed");
}
}
//Binary tree to find the node to be deleted
public Node search(int value){
if(root == null){
return null;
}else{
return this.root.search(value);
}
}
//Parent tree of node to be deleted
public Node searchParent(int value){
if(root == null){
return null;
}else{
return this.root.searchParent(value);
}
}
//Binary tree finds the smallest node with the current node as the root node
public int delRightTreeMin(Node node){
Node target = node;
//Binary sort tree can find the left node circularly
while(target.left != null){
target = target.left;
}
//The smallest node is found when you exit the loop
//Delete minimum node
deleteNode(target.value);
return target.value;
}
//Delete node from binary tree
public void deleteNode(int value){
if(this.root == null){
return;
}else{
//Find the node to be deleted
Node targetNode = search(value);
//No node to be deleted found
if(targetNode == null){
return;
}
//The following code defaults to targetnode= null
if(this.root.left == null && this.root.right == null){
//targetNode == root
root = null;
return;
}
//The following code defaults to targetnode= null && targetNode != root
//Find the parent node of targetNode
Node parent = searchParent(value);
if(targetNode.left == null && targetNode.right == null){
//The node to be deleted is a leaf node
//Judge the relationship between the current node and the parent node
if(parent.left != null && parent.left.value == value){
//Left child node
parent.left = null;
}else if(parent.right != null && parent.right.value == value){
//Right child node
parent.right = null;
}
}else if(targetNode.left != null && targetNode.right != null){
//There are left and right subtrees for the node to be deleted
int minValue = delRightTreeMin(targetNode.right);
targetNode.value = minValue;
}else{
//The node to be deleted has left subtree or right subtree
if(targetNode.left != null){
//The node to be deleted has a left subtree
if(parent != null){
if(parent.left.value == value){
parent.left = targetNode.left;
}else{
parent.right = targetNode.left;
}
}else{
root = targetNode.left;
}
}else{
//The node to be deleted has a right subtree
if(parent != null){
if(parent.left.value == value){
parent.left = targetNode.right;
}else{
parent.right = targetNode.right;
}
}else{
root = targetNode.right;
}
}
}
}
}
}
public class BinarySortTreeDemo {
public static void main(String[] args) {
int[] array = new int[]{7, 3, 10, 12, 5, 1, 9};
//Create a binary tree object
BinarySortTree bst = new BinarySortTree();
//Add node object
for(Integer temp:array){
bst.add(new Node(temp));
}
//Middle order traversal
System.out.println("Middle order traversal:----");
bst.infixOrder();
//Test delete leaf node
bst.deleteNode(1);
bst.deleteNode(5);
bst.deleteNode(10);
bst.deleteNode(12);
bst.deleteNode(3);
bst.deleteNode(9);
bst.deleteNode(7);
System.out.println("After deleting a node:------");
bst.infixOrder();
}
}
Middle order traversal:----
Node{value=1}
Node{value=3}
Node{value=5}
Node{value=7}
Node{value=9}
Node{value=10}
Node{value=12}
After deleting a node:------
Empty tree cannot be traversed
Balanced binary tree
Requirements:
Give you a sequence {1,2,3,4,5,6}, ask to create a binary sort tree (BST), and analyze the problem
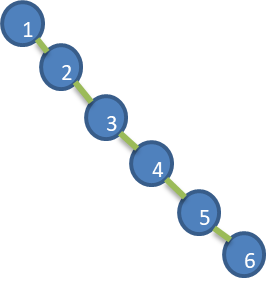
Analysis of problems in BST
- The left subtree is all empty. From the formal point of view, it is more like a single linked list
- Insertion speed has no effect
- The query speed is significantly reduced (because it needs to be compared in turn), which can not give full play to the advantages of BST
It needs to be solved by using balanced binary (search) tree
Basic introduction:
Balanced binary tree is also called self balancing binary search tree, also known as AVL tree, which can ensure high query efficiency.
It has the following characteristics: it is an empty tree or the absolute value of the height difference between its left and right subtrees does not exceed 1, and both the left and right subtrees are a balanced binary tree. Adding and deleting may require rebalancing the tree through one or more tree rotations
The common implementation methods of balanced binary tree include red black tree, AVL, scapegoat tree, tree, extension tree and so on
Application case - left rotation
Requirements: give you a sequence of numbers and create the corresponding balanced binary tree Sequence {4,3,6,5,7,8}
Train of thought analysis

Note: insert the left subtree of node 6 to the right of node 4, and set node 6 as the root node
//Take this as the root node to rotate the binary tree to the left
public void leftRotate(){
//Create a new node attribute, which is the attribute of the root node of the current binary tree
Node newNode = new Node(this.value);
//The left subtree of the new node is set as the left subtree of the current node
newNode.left = this.left;
//The right subtree of the new node is set as the left subtree of the right subtree of the current node
newNode.right = this.right.left;
//Replace the attribute of the current node with the attribute of the right child node
this.value = this.right.value;
//The right subtree of the current node is set as the right subtree of the right subtree of the current node
this.right = this.right.right;
//The left subtree of the current node is set as the new node
this.left = newNode;
}
Application case - right rotation
Requirements: give you a sequence of numbers to create the corresponding balanced binary tree Sequence {10,12,8,9,7,6}
Train of thought analysis:
 Note: insert the right subtree of node 8 to the left of node 10, and set node 8 as the root node
Note: insert the right subtree of node 8 to the left of node 10, and set node 8 as the root node
//Rotate the binary tree right with this as the root node
public void rightRotate(){
//Create a new node attribute and set it as the attribute of the root node of the current binary tree
Node newNode = new Node(this.value);
//The right subtree of the new node is set as the right subtree of the current node
newNode.right = this.right;
//The left subtree of the new node is set as the right subtree of the left subtree of the current node
newNode.left = this.left.right;
//Replace the attributes of the current node with the attributes of the left child node
this.value = this.left.value;
//The left subtree of the current node is set as the left subtree of the left subtree of the current node
this.left = this.left.left;
//The right subtree of the current node is set as the new node
this.right = newNode;
}
Application case - double rotation
Problem: in some cases, single rotation cannot complete the conversion of balanced binary tree
int[] arr = { 10, 11, 7, 6, 8, 9 }; Running the original code, you can see that it is not converted into AVL tree
int[] arr = {2,1,6,5,7,3}; // Running the original code, you can see that it is not converted into AVL tree
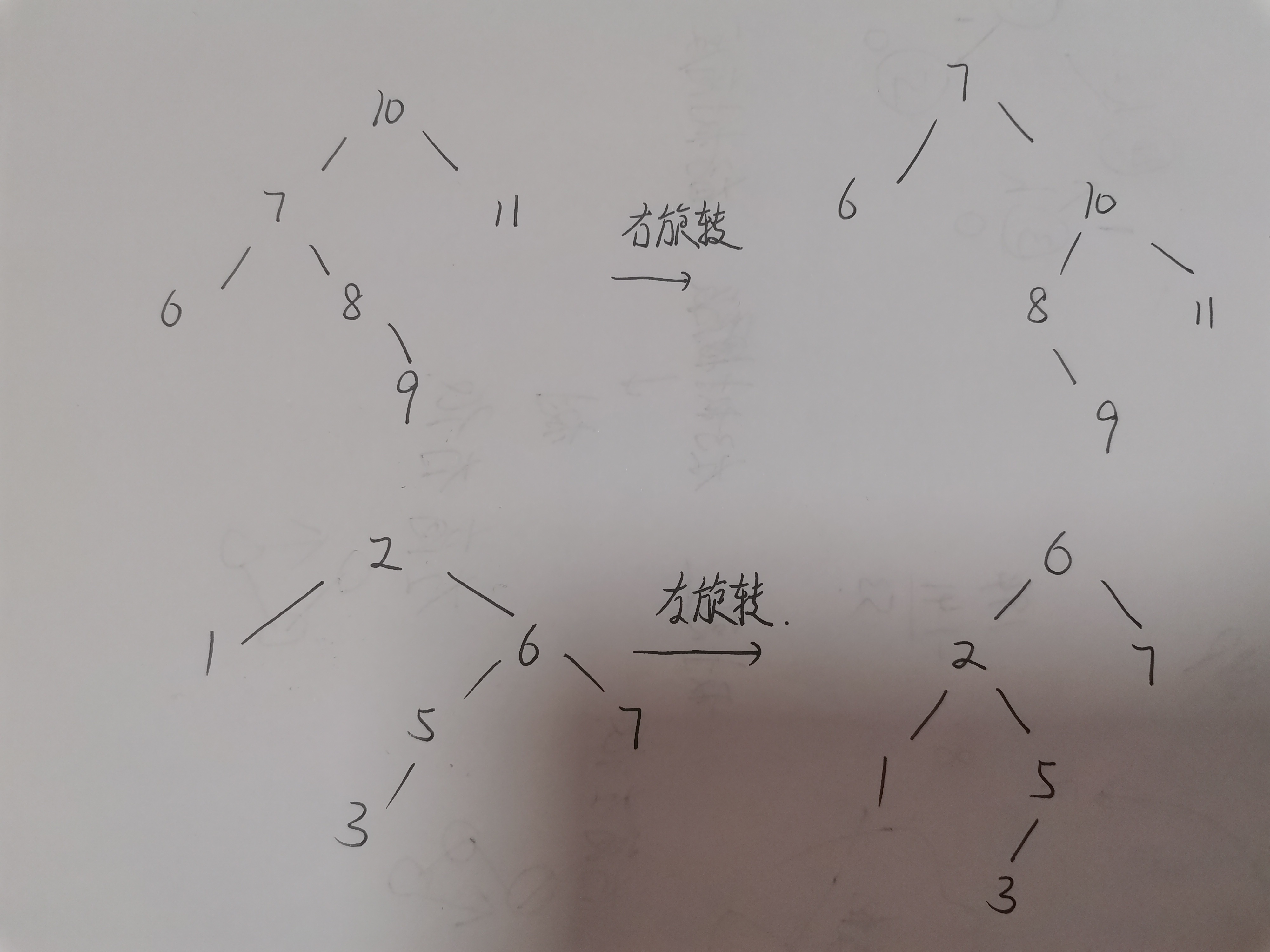
resolvent:
Int [] arr = {10, 11, 7, 6, 8, 9} insert node 9
- When the binary tree with this as the root node satisfies the right rotation
- Check: the height of the right subtree of the left subtree of this is greater than the height of the left subtree of the left subtree of this
- First, rotate the left subtree of this
- Then rotate this right
int[] arr = {2,1,6,5,7,3} insert node 3
- When the binary tree with this as the root node satisfies the left rotation
- Check: the height of the left subtree of the right subtree of this is greater than the height of the right subtree of the right subtree of this
- First rotate the right subtree of this
- Then rotate this to the left
Code display:
package com.atguigu.avl;
import java.util.Arrays;
/**
* @ClassName AVLTreeDemo
* @Author Jeri
* @Date 2022-02-27 10:14
* @Description Construction of balanced binary tree
*/
//Create node class
class Node{
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
//Override toString()
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
//Middle order traversal
public void infixOrder(){
if(this.left != null){
this.left.infixOrder();
}
System.out.println(this);
if(this.right != null){
this.right.infixOrder();
}
}
//Add node
public void add(Node node){
//Handling special situations
if(node == null){
return;
}
//Judge node Value and this Value size relationship
if(this.value > node.value){
//Add left
if(this.left == null){
this.left = node;
}else{
this.left.add(node);
}
}else{
//Add right
if(this.right == null){
this.right = node;
}else{
this.right.add(node);
}
}
//Balance after adding nodes
if(this.leftHeight() - this.rightHeight() > 1){
//(height of left subtree - height of right subtree) > 1 rotate right
if(this.left != null &&
this.left.rightHeight() > this.left.leftHeight()){
//The height of the right subtree of the left subtree of this > the height of the left subtree of the left subtree of this
//Rotate the left subtree of this
this.left.leftRotate();
//this makes a right rotation
this.rightRotate();
}else{
//this makes a right rotation
this.rightRotate();
}
return;
}
if(this.rightHeight() - this.leftHeight() > 1){
//(height of right subtree - height of left subtree) > 1 rotate left
if(this.right != null &&
this.right.leftHeight() > this.right.rightHeight()){
//The height of the left subtree of the right subtree of this > the height of the right subtree of the right subtree of this
//Right rotation of the right subtree of this
this.right.rightRotate();
//Rotate this left
this.leftRotate();
}else{
//Rotate this left
this.leftRotate();
}
return;
}
}
//Returns the height of the tree with this as the root node
public int height(){
return Math.max(this.left == null?0:this.left.height(),
this.right == null?0:this.right.height()) + 1;
}
//Returns the height of the left subtree with this as the root node
public int leftHeight(){
if(this.left == null){
return 0;
}
return this.left.height();
}
//Returns the height of the right subtree with this as the root node
public int rightHeight(){
if(this.right == null){
return 0;
}
return this.right.height();
}
//Take this as the root node to rotate the binary tree to the left
public void leftRotate(){
//Create a new node attribute, which is the attribute of the root node of the current binary tree
Node newNode = new Node(this.value);
//The left subtree of the new node is set as the left subtree of the current node
newNode.left = this.left;
//The right subtree of the new node is set as the left subtree of the right subtree of the current node
newNode.right = this.right.left;
//Replace the attribute of the current node with the attribute of the right child node
this.value = this.right.value;
//The right subtree of the current node is set as the right subtree of the right subtree of the current node
this.right = this.right.right;
//The left subtree of the current node is set as the new node
this.left = newNode;
}
//Rotate the binary tree right with this as the root node
public void rightRotate(){
//Create a new node attribute and set it as the attribute of the root node of the current binary tree
Node newNode = new Node(this.value);
//The right subtree of the new node is set as the right subtree of the current node
newNode.right = this.right;
//The left subtree of the new node is set as the right subtree of the left subtree of the current node
newNode.left = this.left.right;
//Replace the attributes of the current node with the attributes of the left child node
this.value = this.left.value;
//The left subtree of the current node is set as the left subtree of the left subtree of the current node
this.left = this.left.left;
//The right subtree of the current node is set as the new node
this.right = newNode;
}
}
//Create balance tree
class AVLTree{
private Node root;
public Node getRoot() {
return root;
}
public void setRoot(Node root) {
this.root = root;
}
//Add node to balance tree
public void add(Node node){
if(this.root == null){
this.root = node;
}else{
this.root.add(node);
}
}
//Order traversal in balanced tree
public void infixOrder(){
if(this.root == null){
System.out.println("Empty tree cannot be traversed");
}else{
this.root.infixOrder();
}
}
}
public class AVLTreeDemo {
public static void main(String[] args) {
//int[] arr = {4,3,6,5,7,8};
//int[] arr = {2,1,6,5,7,3};
int[] arr = { 10, 11, 7, 6, 8, 9 };
System.out.println("Original array:-----");
System.out.println(Arrays.toString(arr));
//Create an AVLTree object
AVLTree avlTree = new AVLTree();
//Add node
for(int i=0; i < arr.length; i++) {
avlTree.add(new Node(arr[i]));
}
//ergodic
System.out.println("Middle order traversal");
avlTree.infixOrder();
System.out.println("In balance processing~~");
System.out.println("Current root node=" + avlTree.getRoot());
System.out.println("Height of tree=" + avlTree.getRoot().height());
System.out.println("Height of the left subtree of the tree=" + avlTree.getRoot().leftHeight());
System.out.println("Height of right subtree of tree=" + avlTree.getRoot().rightHeight());
}
}
Original array:-----
[10, 11, 7, 6, 8, 9]
Middle order traversal
Node{value=6}
Node{value=7}
Node{value=8}
Node{value=9}
Node{value=10}
Node{value=11}
In balance processing~~
Current root node=Node{value=8}
Height of tree=3
Height of the left subtree of the tree=2
Height of right subtree of tree=2
Original array:-----
[2, 1, 6, 5, 7, 3]
Middle order traversal
Node{value=1}
Node{value=2}
Node{value=3}
Node{value=5}
Node{value=6}
Node{value=7}
In balance processing~~
Current root node=Node{value=5}
Height of tree=3
Height of the left subtree of the tree=2
Height of right subtree of tree=2