Heap sort
Basic introduction
-
Heap sort is a sort algorithm designed by using the data structure of heap. Heap sort is a selective sort. Its worst, best, average time complexity is O(nlogn), and it is also an unstable sort.
-
Heap is a complete binary tree with the following properties: the value of each node is greater than or equal to the value of its left and right child nodes, which is called large top heap. Note: there is no size relationship between the value of the left child and the value of the right child of the node.
-
The value of each node is less than or equal to the value of its left and right child nodes, which is called small top heap
-
Large top reactor
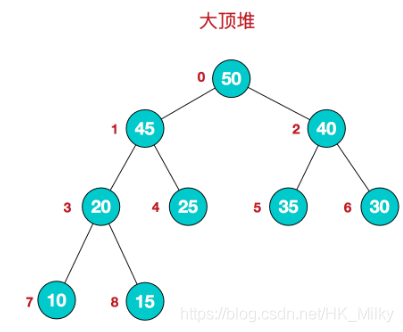

Features of large top stack: arr [i] > = arr [2 * I + 1] & & arr [i] > = arr [2 * I + 2] / / I corresponds to several nodes, and I starts from 0
-
Small top pile
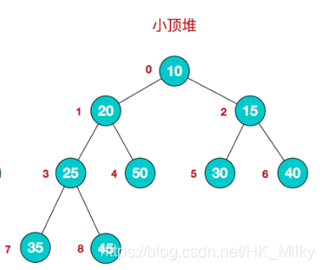
Characteristics of small top pile: arr [i] < = arr [2 * I + 1] & & arr [i] < = arr [2 * I + 2] / / I corresponds to several nodes, I starts from 0
-
Generally, large top pile is used in ascending order and small top pile is used in descending order
- The basic idea of heap sorting is:
- The sequence to be sorted is constructed into a large top heap
- At this point, the maximum value of the whole sequence is the root node at the top of the heap.
- Swap it with the end element, where the end is the maximum.
- Then reconstruct the remaining n-1 elements into a heap, which will get the sub small value of n elements. If you execute it repeatedly, you can get an ordered sequence.
Train of thought analysis
Step 1: construct the initial heap. The given disordered sequence is constructed into a large top heap (generally, the large top heap is used in ascending order and the small top heap is used in descending order).
-
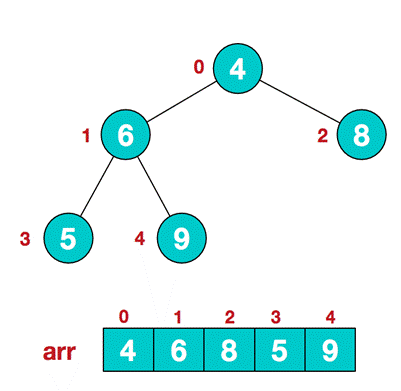
. Suppose that the structure of a given unordered sequence is as follows
-
. At this time, we start from the last non leaf node (the leaf node does not need to be adjusted naturally. The first non leaf node arr.length/2-1=5/2-1=1, that is, the following 6 nodes), and adjust from left to right and from bottom to top.
-
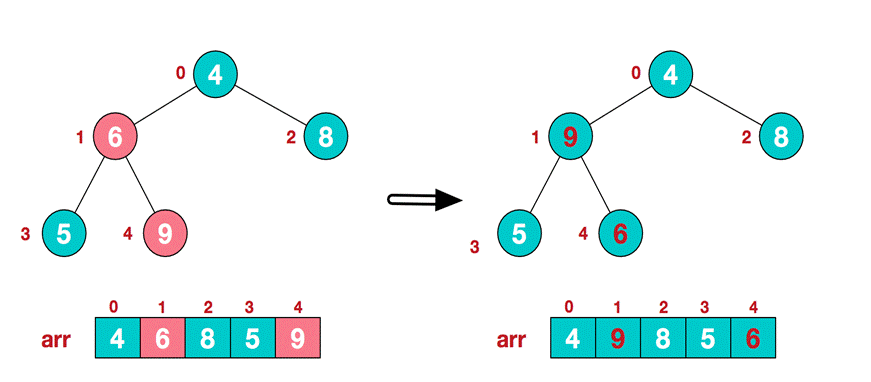
. Find the second non leaf node 4. Since the 9 element in [4,9,8] is the largest, 4 and 9 exchange.
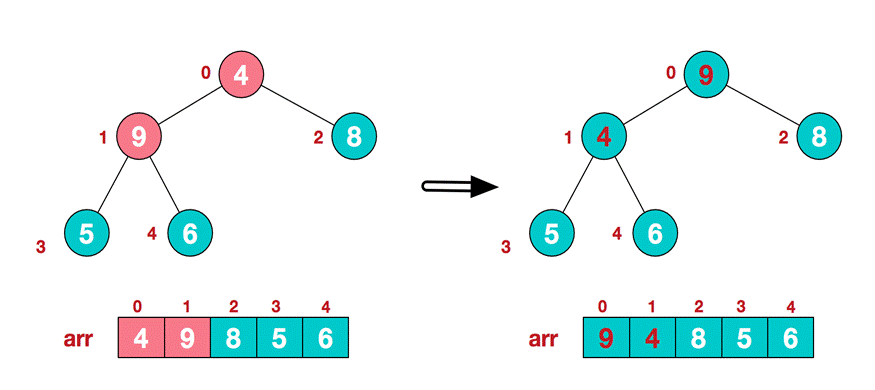
-
At this time, the exchange leads to the confusion of the structure of the sub root [4,5,6]. Continue to adjust. 6 is the largest in [4,5,6], and exchange 4 and 6.
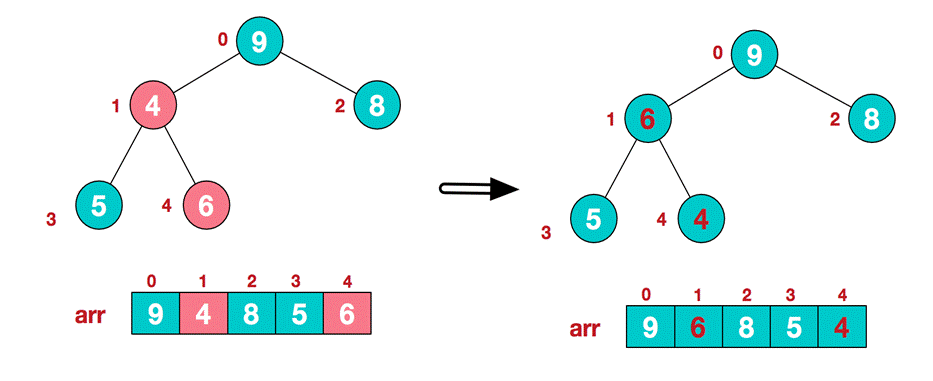
At this point, we construct an unordered sequence into a large top heap.
In step 2, the top element of the heap is exchanged with the last element to maximize the last element. Then continue to adjust the heap, and then exchange the top element with the end element to get the second largest element. Such repeated exchange, reconstruction and exchange.
-
. Swap top element 9 and end element 4
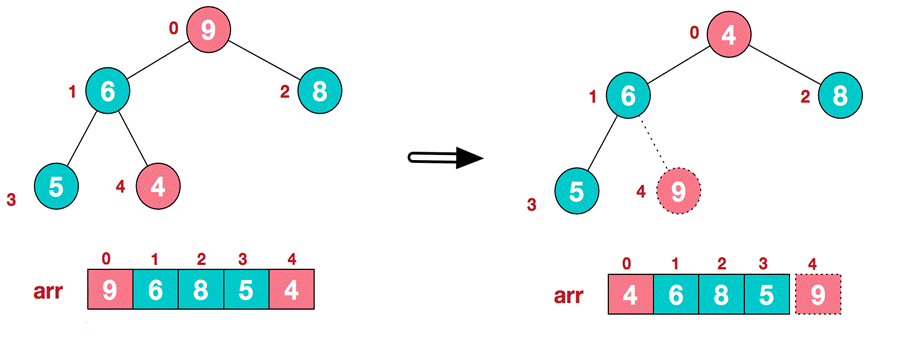
-
. Restructure so that it continues to meet the heap definition
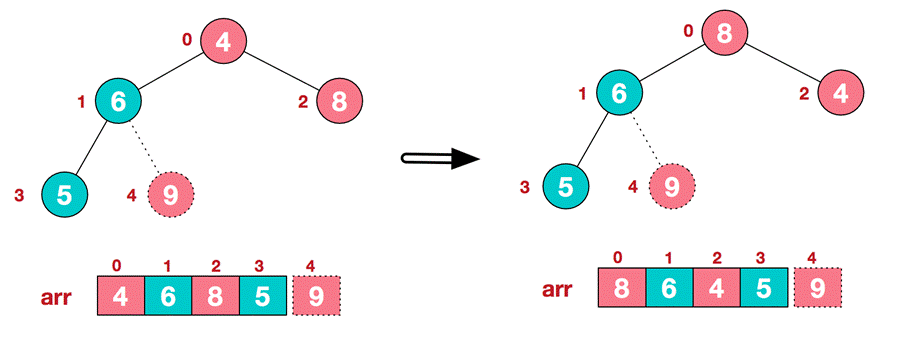
-
. Then exchange the top element 8 with the end element 5 to obtain the second largest element 8
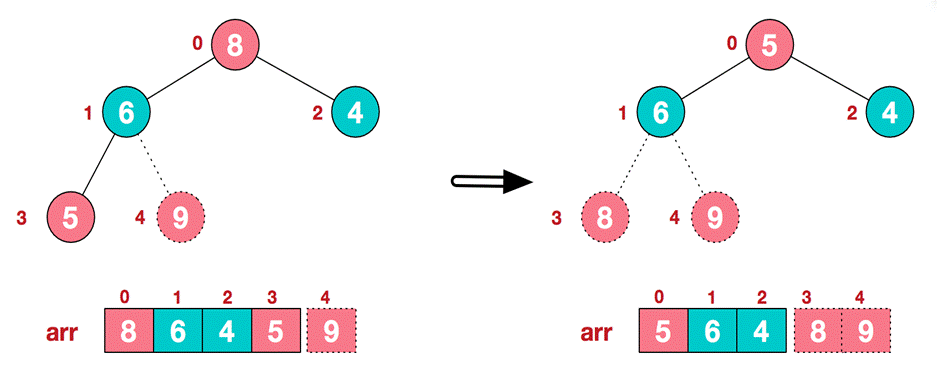
-
In the subsequent process, continue to adjust and exchange, so as to make the whole sequence orderly
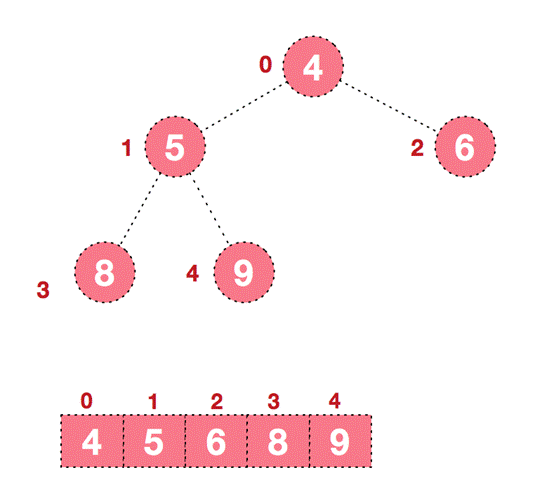
Then briefly summarize the basic idea of heap sorting:
1). The unordered sequence is constructed into a heap, and the large top heap or small top heap is selected according to the ascending and descending requirements;
2). Exchange the top element with the end element, and "sink" the largest element to the end of the array;
3). Readjust the structure to meet the heap definition, then continue to exchange the heap top elements with the current tail elements, and repeat the adjustment + exchange steps until the whole sequence is in order.
Code display
package demo06;
import java.util.Arrays;
public class HeapSort {
public static void main(String[] args) {
//Requires the array to be sorted in ascending order
int arr[] = {4,6,8,5,9,-1,44,2,7};
heapSort(arr);
}
//Write a heap sorting method
public static void heapSort(int[] arr) {
int temp=0;
System.out.println("Heap sort!!!");
// Step by step
// adjustHeap(arr,1,arr.length);
// System.out.println("first time" + Arrays.toString(arr));
//
// adjustHeap(arr,0,arr.length);
// System.out.println("second time" + Arrays.toString(arr));
//Complete final code
//1. Build an unordered sequence into a heap, and select a large top heap or a small top heap according to the ascending and descending requirements
for (int i = arr.length / 2 - 1; i >= 0; i--) {
adjustHeap(arr, i, arr.length);
}
//2. Swap the top element with the end, and "sink" the largest element to the end of the array
//3. Readjust the structure to meet the heap definition, then continue to exchange the heap top element and the current tail element, and repeat steps 2 and 3 until the whole sequence is in order
for (int j = arr.length - 1; j > 0; j--) {
//exchange
temp=arr[j];
arr[j]=arr[0];
arr[0]=temp;
adjustHeap(arr,0,j);
}
System.out.println("array=" + Arrays.toString(arr));
}
//Adjust an array (binary tree) to a large top heap
/**
* Function: adjust the tree of non leaf nodes corresponding to i pointed to by i into a large top heap
* For example: int [] arr = {4,6,8,5,9} = > I = 1 = > adjustheap = > get {4,9,8,5,6}
* If we adjust adjustHeap again, the input is I = 0 = > so that {4,9,8,5,6} = > {9,6,8,5,4}
*
* @param arr Array to be adjusted
* @param i Represents the index of a non leaf node in the array
* @param length Indicates how many elements are adjusted, and the length is gradually decreasing
*/
public static void adjustHeap(int[] arr, int i, int length) {
int temp = arr[i];//First, take out the value of the current element and save it in a temporary variable
//Start adjustment
//explain
//1. K = i * 2 + 1 K is the left child node of i
for (int k = i * 2 + 1; k < length; k = k * 2 + 1) {
if (k + 1 < length && arr[k] < arr[k + 1]) {//Indicates that the value of the left child node is less than that of the right child node
k++; //k points to the right child node
}
if (arr[k] > temp) { //If the child node is larger than the parent node
arr[i] = arr[k]; //Assign a larger value to the current node
i = k; //!!!! i points to k to continue cyclic comparison
} else {
break;
}
}
//When the for loop ends, we have placed the maximum value of the tree with i as the parent node at the top (local)
arr[i] = temp; //Put the temp value in the adjusted position
}
}
huffman tree
Basic introduction
- Given n weights as n leaf nodes, a binary tree is constructed. If the weighted path length (wpl) of the tree reaches the minimum, such a binary tree is called the optimal binary tree, also known as Huffman tree. Other books are translated as Huffman tree.
- Huffman tree is the tree with the shortest weighted path length, and the node with larger weight is closer to the root.
Several concepts
- Path and path length: the path between child or grandson nodes that can be reached from one node down in a tree is called path. The number of branches in a path is called the path length. If the specified number of layers of the root node is 1, the path length from the root node to the L-th layer node is L-1
- Node weight and weighted path length: if a node in the tree is assigned a value with a certain meaning, this value is called the weight of the node. The weighted path length of a node is the product of the path length from the root node to the node and the weight of the node
- Weighted path length of the tree: the weighted path length of the tree is specified as the sum of the weighted path lengths of all leaf nodes, which is recorded as WPL(weighted path length). The binary tree with greater weight and closer to the root node is the optimal binary tree.
- The smallest WPL is Huffman tree
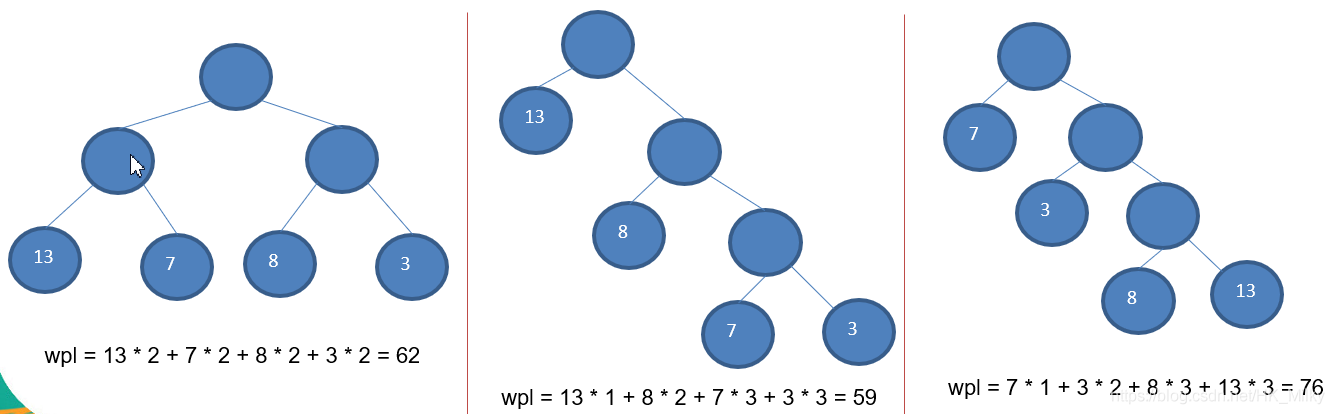
Train of thought analysis
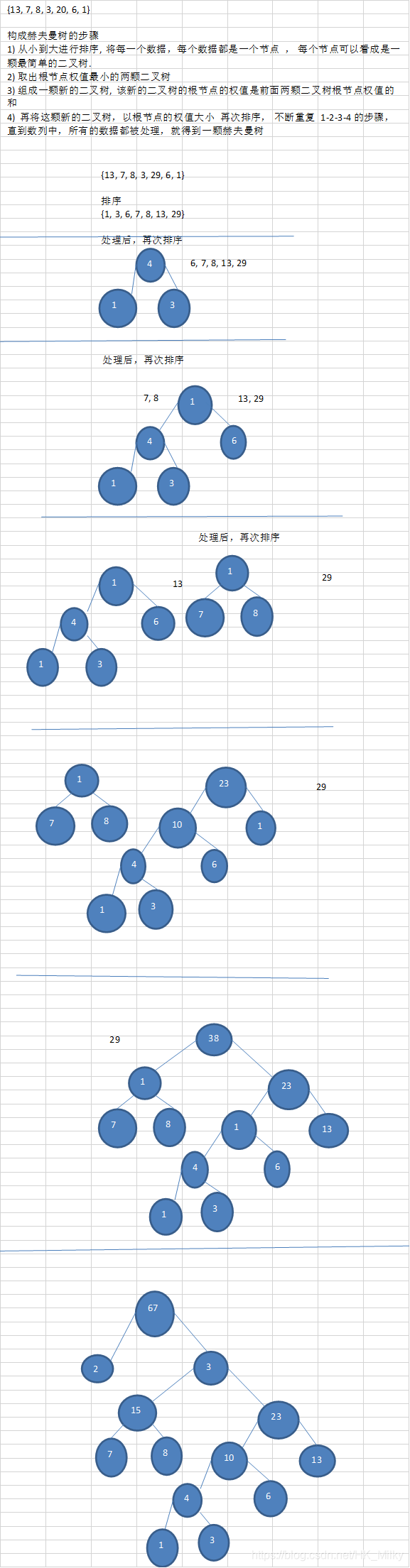
Steps to form Huffman tree:
- Sort from small to large. Each data is a node, and each node can be regarded as the simplest binary tree
- Take out the two binary trees with the smallest weight of the root node
- Form a new binary tree. The weight of the root node of the new binary tree is the sum of the weight of the root node of the previous two binary trees
- The new binary tree is sorted again according to the weight of the root node, and the steps of 1-2-3-4 are repeated until all the data in the sequence are processed to obtain a Huffman tree
code analysis
package demo01;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class HuffmanTree {
public static void main(String[] args) {
int[] arr = {13, 7, 8, 3, 29, 6, 1};
Node root = createHuffmanTree(arr);
//Test one
preOrder(root);
}
public static void preOrder(Node root){
if (root!=null){
root.preOrder();
}else {
System.out.println("The tree is empty");
}
}
//Method of creating Huffman tree
public static Node createHuffmanTree(int[] arr) {
//The first step is to facilitate operation
//1. Traverse the arr array
//2. Form each element of arr into a Node
//3. Put the Node into the ArrayList
List<Node> nodes = new ArrayList<>();
for (int value : arr) {
nodes.add(new Node(value));
}
//The process we deal with is a circular process
while (nodes.size() > 1) {
//Sort from small to large
Collections.sort(nodes);
System.out.println(nodes);
//Take out the two binary trees with the smallest weight of the root node
//(1) Take out the node with the smallest weight (binary tree)
Node leftNode = nodes.get(0);
//(1) Take out the node with the second smallest weight (binary tree)
Node rightNode = nodes.get(1);
//(3) Construct a new binary tree
Node parent = new Node(leftNode.value + rightNode.value);
parent.left = leftNode;
parent.right = rightNode;
//(4) Delete the processed binary tree from the ArrayList
nodes.remove(leftNode);
nodes.remove(rightNode);
//(5) Add parent to nodes
nodes.add(parent);
Collections.sort(nodes);
}
return nodes.get(0);
}
}
//Create node
//In order to keep the Node objects sorted, the Collections collection is sorted
//Let Node implement Comparable interface
class Node implements Comparable<Node> {
int value; //Node weight
Node left; //Point to left child node
Node right; //Point to the right child node
public Node(int value) {
this.value = value;
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
@Override
public int compareTo(Node o) {
//Ascending order from small to large
return this.value - o.value;
}
//Write a preorder traversal
public void preOrder(){
System.out.println(this);
if(this.left!=null){
this.left.preOrder();
}
if(this.right!=null){
this.right.preOrder();
}
}
}
Huffman coding
Basic introduction
- Huffman coding, also known as Huffman coding, also known as Huffman coding, is a coding method and belongs to a program algorithm
- Huffman coding is one of the classical applications of Huffman tree in telecommunications
- Huffman coding is widely used in data file compression. The compression ratio is usually between 20% ~ 90%
- Huffman code is a kind of variable word length coding (VLC). Huffman proposed a coding method in 1952, which is called optimal coding
Principle analysis
1. Fixed length coding
- i like like like java do you like a java / / 40 characters in total (including spaces) convert to ACSII code
- 105 32 108 105 107 101 32 108 105 107 101 32 108 105 107 101 32 106 97 118 97 32 100 111 32 121 111 117 32 108 105 107 101 32 97 32 106 97 118 97 / / corresponding Ascii code
- 01101001 00100000 01101100 01101001 01101011 01100101 00100000 01101100 01101001 01101011 01100101 00100000 01101100 01101001 01101011 01100101 00100000 01101010 01100001 01110110 01100001 00100000 01100100 01101111 00100000 01111001 01101111 01110101 00100000 01101100 01101001 01101011 01100101 00100000 01100001 00100000 01101010 01100001 0111011 0 0110001 / / corresponding binary
- Information is passed in binary, with a total length of 359 (including spaces)
- Online transcoding tool: https://www.mokuge.com/tool/asciito16/
2. Variable length coding
- i like like like java do you like a java / / a total of 40 characters (including spaces)
- d: 1 y: 1 u: 1 J: 2 V: 2 O: 2 L: 4 K: 4 E: 4 I: 5 A: 5: 9 / / number of characters
- 0 = (space), 1=a, 10=i, 11=e, 100=k, 101=l, 110=o, 111=v, 1000=j, 1001=u, 1010=y, 1011=d
Note: code according to the occurrence times of each character. In principle, the more the occurrence times, the smaller the code. For example, if the space appears 9 times, the code is 0, and so on - According to the code specified for each character above, when we transmit "i like like like java do you like a java" data, the code is
10010110100... - Character codes cannot be prefixes of other character codes. Codes that meet this requirement are called prefix codes, that is, duplicate codes cannot be matched
3. Huffman coding
-
Transmitted string i like like like java do you like a java
-
d:1. y:1, u:1, j:2, v:2, o:2, l:4, k:4, e:4, i:5, a:5, (space): 9 / / the number of characters corresponding to each character
-
A Huffman tree is constructed according to the number of occurrences of the above characters, and the number is used as the weight
- Steps to form Huffman tree:
- Sort from small to large. Each data is a node, and each node can be regarded as the simplest binary tree
- Take out the two binary trees with the smallest weight of the root node
- Form a new binary tree. The weight of the root node of the new binary tree is the sum of the weight of the root node of the previous two binary trees
- The new binary tree is sorted again according to the weight of the root node, and the steps of 1-2-3-4 are repeated until all the data in the sequence are processed to obtain a Huffman tree
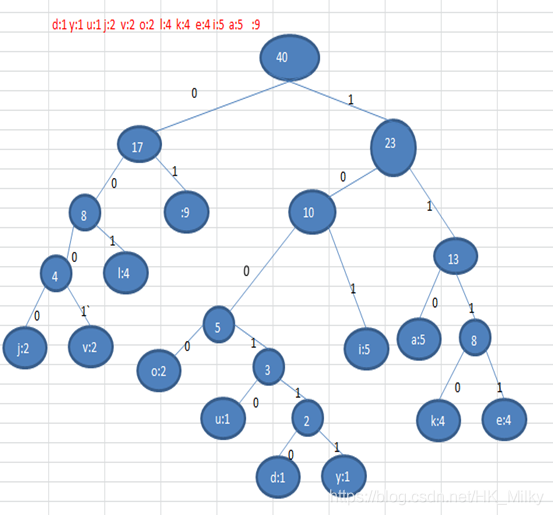
-
According to the Huffman tree, each character is coded (prefix coding). The path to the left is 0 and the path to the right is 1. The coding is as follows:
o: 1000 u: 10010 d: 100110 y: 100111 i: 101 a : 110 k: 1110 e: 1111
j: 0000 v: 0001 l: 001 (space): 01 -
According to the Huffman code above, the corresponding code of our "i like like like java do you like a java" string is (note the lossless compression we use here)
101010011111011111010011111011111010011111010011111010000110000111001100111100001100111100010011011110111111111101111001011111111110111100100001100001110 is processed by Huffman coding, and the length is 133 -
Length: 133
Note: the original length is 359, compressed (359-133) / 359 = 62.9%
This code meets the prefix code, that is, the code of characters cannot be the prefix of other character codes. It will not cause polysemy of matching
Huffman coding is a lossless processing scheme
Note: the Huffman tree may be different according to different sorting methods, so the corresponding Huffman codes are not exactly the same, but wpl is the same and the minimum, and the length of the finally generated Huffman code is the same. For example, if we make the new binary tree generated every time always rank last in the binary tree with the same weight, the generated binary tree is:

Application of Huffman tree
Practical operation
Data compression (generating Huffman tree)
A text to be given, such as "i like like like java do you like a java" , According to the Huffman coding principle mentioned above, data compression processing is carried out for it in the form of "1010100110111101111010011011110111101001101111011110100001100001110011001111000011001111000100100100110111101111011100100001100001110 " Step 1: according to the principle of Huffman encoded compressed data, you need to create "i like like like java do you like a java" Corresponding Huffman tree.
Data compression (generating Huffman coding and Huffman coded data)
We have generated the Huffman tree, Now let's continue to complete the task 1.Generate Huffman coding corresponding to Huffman tree , See the table below:=01 a=100 d=11000 u=11001 e=1110 v=11011 i=101 y=11010 j=0010 k=1111 l=000 o=0011 2.Huffman coding is used to generate Huffman coded data ,That is, according to the Huffman code above"i like like like java do you like a java" String generates the corresponding encoded data, Under form. 1010100010111111110010001011111111001000101111111100100101001101110001110000011011101000111100101000101111111100110001001010011011100
Data decompression (decoding with Huffman encoding)
Use Huffman coding to decode data. The specific requirements are 1.Previously, we obtained Huffman code and corresponding code byte[] , Namely:[-88, -65, -56, -65, -56, -65, -55, 77, -57, 6, -24, -14, -117, -4, -60, -90, 28] 2.Now it is required to use Huffman coding to decode and get the original string again"i like like like java do you like a java"
File compression
read file-> Get Huffman coding table -> Complete compression
File decompression
Read compressed file(Data and Huffman coding table)-> Complete decompression(File recovery)
matters needing attention
1.If the file itself is compressed, the recompression efficiency using Huffman coding will not change significantly, Like video,ppt Wait, file 2.Huffman encoding is processed by bytes, so it can process all files(Binary file, text file) 3.If there is not much duplicate data in a file, the compression effect will not be obvious.
code implementation
package demo01;
import java.io.*;
import java.util.*;
public class HuffmanCode {
public static void main(String[] args) {
/*
String content = "i like like like java do you like a java";
byte[] contentBytes = content.getBytes();
System.out.println(contentBytes.length); //40
//code
byte[] huffmanZipBytes = huffmanZip(contentBytes);
System.out.println(Arrays.toString(huffmanZipBytes));
//How to decompress (decode) data
byte[] sourceBytes = decode(huffmanCodes, huffmanZipBytes);
System.out.println("Original string = "+ new String(sourceBytes));
*/
/*
//Test compressed file
String srcFile="F:\\alphonse.jpg";
String dstFile="F:\\alphonse.zip";
zipFile(srcFile,dstFile);
System.out.println("Compression succeeded ~ ~ ");
*/
//Test extract file
String zipFile="F:\\alphonse.zip";
String dstFile="F:\\alphonse1.jpg";
unZipFile(zipFile,dstFile);
System.out.println("Decompression succeeded~~");
}
//Write a method to compress a file
public static void zipFile(String srcFile, String dstFile) {
//Create output stream
FileOutputStream os = null;
ObjectOutputStream oos = null;
//Create an input stream for the file
FileInputStream is = null;
try {
is = new FileInputStream(srcFile);
//Create a byte [] with the same size as the source file
byte[] b = new byte[is.available()];
//read file
is.read(b);
//Compress source files directly
byte[] huffmanZipBytes = huffmanZip(b);
//Create the output stream of the file and store the compressed file
os = new FileOutputStream(dstFile);
//Create an ObjectOutputStream associated with the file output stream
oos = new ObjectOutputStream(os);
//Write the byte array encoded by Huffman into the compressed file
oos.writeObject(huffmanZipBytes);
//Here we write Huffman code in the form of object stream for later use when we recover the source file
//Note: be sure to write Huffman code into the compressed file
oos.writeObject(huffmanCodes);
} catch (Exception e) {
e.printStackTrace();
} finally {
try {
is.close();
oos.close();
os.close();
} catch (IOException e) {
e.printStackTrace();
}
}
}
//Write a method to decompress the compressed file
/**
* @param zipFile Ready to unzip files
* @param dstFile Unzip the file to that path
*/
public static void unZipFile(String zipFile,String dstFile){
//Define the input stream of the file
InputStream is =null;
//Define an object input stream
ObjectInputStream ois=null;
//Define the output stream of the file
OutputStream os=null;
try {
//Create file input stream
is=new FileInputStream(zipFile);
//Create an object input stream associated with is
ois = new ObjectInputStream(is);
//Read byte array to huffmanBytes
byte[] huffmanBytes=(byte[])ois.readObject();
//Read Huffman coding table
Map<Byte,String> huffmanCodes=(Map<Byte,String>)ois.readObject();
//decode
byte[] decode = decode(huffmanCodes, huffmanBytes);
//Writes the bytes array to the target file
os=new FileOutputStream(dstFile);
//Write data to file
os.write(decode);
} catch (Exception e) {
e.printStackTrace();
} finally {
try {
os.close();
ois.close();
is.close();
} catch (IOException e) {
e.printStackTrace();
}
}
}
//Complete data decompression
//thinking
//1. Insert [- 88, - 65, - 56, - 65, - 56, - 65, - 55, 77, - 57, 6, - 24, - 14, - 117, - 4, - 60, - 90, 28]
// First, convert it to the binary string corresponding to Huffman code "101010011111011101111011..."
//2. Binary string corresponding to Huffman code "10101001111101111010... = > Re convert to string according to Huffman code = > "I like like like Java do you like a Java"
/**
* Convert a byte to a binary string
*
* @param b Incoming byte
* @return The returned string is the binary string corresponding to the b (note that it is returned by complement)
* @Param flag Flag whether the high order needs to be supplemented. If true, it means that the high order needs to be supplemented; if false, it means that the high order does not need to be supplemented
*/
private static String byteToBitString(boolean flag, byte b) {
//Save b using variables
int temp = b;//Convert b to int type
//If it's a positive number, we need to fill in the high order
if (flag) {
temp = temp | 256; // Bitwise and 256 1 0000 0000 | 0000 0001 = > 1 0000 0001
}
String str = Integer.toBinaryString(temp); //The binary complement corresponding to temp is returned
if (flag) {
return str.substring(str.length() - 8);
} else {
return str;
}
}
/**
* Write a method to complete the decoding of compressed data
*
* @param huffmanCodes Huffman coding table map
* @param huffmanBytes Huffman encoded byte array
* @return Is the array corresponding to the original string
*/
private static byte[] decode(Map<Byte, String> huffmanCodes, byte[] huffmanBytes) {
//1. First get the binary string corresponding to huffmanBytes, such as 10101001111101111010
StringBuilder stringBuilder = new StringBuilder();
//Convert byte array to binary string
for (int i = 0; i < huffmanBytes.length; i++) {
byte b = huffmanBytes[i];
//Determine whether it is the last byte
boolean flag = (i == huffmanBytes.length - 1);
stringBuilder.append(byteToBitString(!flag, b));
}
System.out.println(stringBuilder.toString());
//Decode the string according to the specified Huffman encoding
//Exchange the Huffman coding table because the reverse query a - > 100 - > a
Map<String, Byte> map = new HashMap<>();
for (Map.Entry<Byte, String> entry : huffmanCodes.entrySet()) {
map.put(entry.getValue(), entry.getKey());
}
//Create a collection to store byte s
List<Byte> list = new ArrayList<>();
//i can be understood as index and scan stringBuilder
for (int i = 0; i < stringBuilder.length(); ) {
int count = 1; //Small counter
boolean flag = true;
Byte b = null;
while (flag) {
//1010100010111111110010001 ...
//Incrementally fetch a '1' or '0'
String key = stringBuilder.substring(i, i + count); // i don't move, let count move, and specify a character to match
b = map.get(key);
if (b == null) {//No match found
count++;
} else {
//Match to
flag = false;
}
}
list.add(b);
i += count; //Let i move directly to the count position
}
//When the for loop ends, we store all the characters in the list
//Put the data in the list into byte [] and return it
byte[] b = new byte[list.size()];
for (int i = 0; i < b.length; i++) {
b[i] = list.get(i);
}
return b;
}
//Use a method to encapsulate the previous method for easy calling
/**
* @param bytes Byte array corresponding to the original string
* @return Is a byte array (compressed array) after Huffman encoding
*/
private static byte[] huffmanZip(byte[] bytes) {
List<Node> nodes = getNodes(bytes);
//Create Huffman tree according to nodes
Node huffmanTreeRoot = createHuffmanTree(nodes);
//Create the corresponding Huffman code according to the Huffman tree
Map<Byte, String> huffmanCodes = getCodes(huffmanTreeRoot);
//According to the generated Huffman code, the compressed Huffman coded byte array is obtained
byte[] huffmanCodeBytes = zip(bytes, huffmanCodes);
return huffmanCodeBytes;
}
//Write a method to return a byte [] compressed by Huffman coding through the generated Huffman coding table
/**
* For example: String content="i like like like java do you like a java"; = " byte[] contentBytes=content.getBytes();
* The returned string is "10101001110111101111101001110111101111101001111101001111101111001000011000011100110011110000110011110001001101111011110111100100001100001110"
* => The corresponding byte [] Huffman codebytes, that is, 8 bits correspond to a byte, which is put into Huffman codebytes
* huffmanCodeBytes[0] = 10101001(Complement) = > byte [derivation 10101001 = < 10101001 - 1 = < 10101000 (inverse) = (the sign bit remains unchanged, others are taken as inverse) 11010111 = - 88] the first bit is the sign bit: 0 is positive and 1 is negative
* huffmanCodeBytes[1] =-88
*
* @param bytes This is the byte [] corresponding to the original string
* @param huffmanCodes huffmanCodes Generated Huffman coded map
* @return Returns the byte [] after Huffman encoding processing
*/
private static byte[] zip(byte[] bytes, Map<Byte, String> huffmanCodes) {
//1. Use Huffman codes to convert bytes into the string corresponding to Huffman code
StringBuilder stringBuilder = new StringBuilder();
//Traversal bytes array
for (byte b : bytes) {
stringBuilder.append(huffmanCodes.get(b));
}
System.out.println("test stringBuilder=" + stringBuilder.toString());
// Set "1010100111110111101011110..." Convert to byte []
//Statistics return byte[] huffmanCodes
//In one sentence, int len = (stringBuilder.length() + 7)/8;
int len;
if (stringBuilder.length() % 8 == 0) {
len = stringBuilder.length() / 8;
} else {
len = stringBuilder.length() / 8 + 1;
}
byte[] huffmanCodeBytes = new byte[len];
int index = 0;//What byte is the record
for (int i = 0; i < stringBuilder.length(); i += 8) { //Because every 8 bits corresponds to a byte, the step size is + 8
String strByte;
if (i + 8 > stringBuilder.length()) {
strByte = stringBuilder.substring(i);
} else {
strByte = stringBuilder.substring(i, i + 8);
}
//Convert strByte into a byte and put it into Huffman codebytes
huffmanCodeBytes[index] = (byte) Integer.parseInt(strByte, 2);
index++;
}
return huffmanCodeBytes;
}
//Generate Huffman coding corresponding to Huffman tree
//thinking
//1. Store Huffman code table in map < byte, string >
// {32=01, 97=100, 100=11000, 117=11001, 101=1110, 118=11011, 105=101, 121=11010, 106=0010, 107=1111, 108=000, 111=0011}
static Map<Byte, String> huffmanCodes = new HashMap<>();
//2. When generating Huffman code table, you need to splice paths and define a StringBuild to store the path of a leaf node
static StringBuilder stringBuilder = new StringBuilder();
//For calling convenience, overload getCodes
private static Map<Byte, String> getCodes(Node root) {
if (root == null) {
return null;
}
//Handle the left subtree of root
getCodes(root.left, "0", stringBuilder);
//Handle the right subtree of root
getCodes(root.right, "1", stringBuilder);
return huffmanCodes;
}
/**
* Function: get the Huffman code of all leaf nodes of the incoming node node and put it into the Huffman code set
*
* @param node Incoming node
* @param code Path: the left child node is 0 and the right child node is 1
* @param stringBuilder For splicing paths
*/
private static void getCodes(Node node, String code, StringBuilder stringBuilder) {
StringBuilder stringBuilder2 = new StringBuilder(stringBuilder);
//Add code to stringBuilder2
stringBuilder2.append(code);
if (node != null) {
//If node equals null, it is not processed
//Judge whether the current node is a leaf node or a non leaf node
if (node.data == null) {
//Recursive processing
//Left recursion
getCodes(node.left, "0", stringBuilder2);
//Recursive right
getCodes(node.right, "1", stringBuilder2);
} else {
//Description is a leaf node
//It means finding the last node of a leaf
huffmanCodes.put(node.data, stringBuilder2.toString());
}
}
}
//Preorder traversal method
private static void preOrder(Node root) {
if (root != null) {
root.preOrder();
} else {
System.out.println("Huffman tree is empty");
}
}
/**
* @param bytes Receive byte array
* @return The returned is list [node {data = 32, weight = 9}, node {data = 97, weight = 5},...]
*/
private static List<Node> getNodes(byte[] bytes) {
//1. Create an ArrayList
ArrayList<Node> nodes = new ArrayList<>();
//2. Traverse bytes and count the number of occurrences of each byte - > map [key, value]
Map<Byte, Integer> counts = new HashMap<>();
for (byte b : bytes) {
Integer count = counts.get(b);
if (count == null) {//At this time, there is no character data in the Map, and the data is stored for the first time
counts.put(b, 1);
} else {
counts.put(b, count + 1);
}
}
//Convert each key value pair into a Node object and add it to the nodes collection
//Traversal map
for (Map.Entry<Byte, Integer> entry : counts.entrySet()) {
nodes.add(new Node(entry.getKey(), entry.getValue()));
}
return nodes;
}
//Create Huffman tree through List
private static Node createHuffmanTree(List<Node> nodes) {
while (nodes.size() > 1) {
//Sort, from small to large
Collections.sort(nodes);
//Take out the first smallest binary tree
Node leftNode = nodes.get(0);
Node rightNode = nodes.get(1);
//Create a new binary tree. Its root node has no data but only weights
Node parent = new Node(null, leftNode.weight + rightNode.weight);
parent.left = leftNode;
parent.right = rightNode;
//Delete the two processed binary trees from nodes
nodes.remove(leftNode);
nodes.remove(rightNode);
//Add a new node to nodes
nodes.add(parent);
}
//The last node of nodes interprets the root node of Huffman tree
return nodes.get(0);
}
}
//Create Node with data and weight
class Node implements Comparable<Node> {
Byte data; //Store data, such as' a '= > 97 and' = > 32
int weight; //Store weight, indicating the number of characters
Node left;
Node right;
public Node(Byte data, int weight) {
this.data = data;
this.weight = weight;
}
@Override
public int compareTo(Node o) {
//Sort from small to large
return this.weight - o.weight;
}
@Override
public String toString() {
return "Node{" +
"data=" + data +
", weight=" + weight +
'}';
}
public void preOrder() {
System.out.println(this);
if (this.left != null) {
this.left.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}
}
Binary sort tree
requirement analysis
Question: give you a sequence (7, 3, 10, 12, 5, 1, 9),It is required to query and add data efficiently
Solution
Ø using arrays
- The array is not sorted. Advantages: it is added directly at the end of the array, which is fast. Disadvantages: slow search speed
- Array sorting, advantages: binary search can be used, which is fast. Disadvantages: in order to ensure the order of the array, when adding new data, after finding the insertion position, the following data needs to move as a whole, which is slow.
Ø use linked storage - linked list
- No matter whether the linked list is orderly or not, the search speed is slow, the speed of adding data is faster than that of the array, and there is no need to move the data as a whole.
Brief introduction
Binary sort tree: BST: (Binary Sort(Search) Tree). For any non leaf node of the binary sort tree, the value of the left child node is required to be smaller than that of the current node, and the value of the right child node is required to be larger than that of the current node.
Special note: if you have the same value, you can put the node on the left child node or the right child node
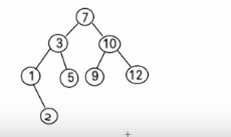
For example, for the previous data (7, 3, 10, 12, 5, 1, 9), the corresponding binary sort tree is:

Creation and traversal of binary sort tree

Deletion of binary sort tree
The deletion of binary sort tree is complex. There are three situations to consider:
-
The first case:
- Delete leaf nodes (for example: 2, 5, 9, 12)
- thinking
- (1) You need to find the targetNode to delete first
- (2) Find the parent node of targetNode
- (3) Determines whether the targetNode is the left child node or the right child node of the parent
- (4) Delete according to the previous situation
- Left child node parent left = null
- Right child node parent right = null;
-
The second case: delete a node with only one subtree, such as 1
- thinking
- (1) You need to find the targetNode to delete first
- (2) Find the parent node of targetNode
- (3) Determines whether the child node of the targetNode is a left child node or a right child node
- (4) Is the targetnode the left child node or the right child node of the parent
- (5) If the targetNode has a left child node
- 5.1 if targetNode is the left child node of parent
- parent.left = targetNode.left;
- 5.2 if the targetNode is the right child node of the parent
- parent.right = targetNode.left;
- (6) If the targetNode has a right child node
- 6.1 if targetNode is the left child node of parent
- parent.left = targetNode.right;
- 6.2 if the targetNode is the right child node of the parent
- parent.right = targetNode.right
-
Case 3: delete a node with two subtrees (e.g. 7, 3, 10)
- thinking
- (1) You need to find the targetNode to delete first
- (2) Find the parent node of targetNode
- (3) Find the smallest node from the right subtree of targetNode
- (4) Use a temporary variable to save the value of the minimum node temp = 11
- (5) Delete the minimum node
- (6) targetNode.value = temp
Code display
package demo01;
public class BinarySortTreeDemo {
public static void main(String[] args) {
int[] arr = {7, 3, 10, 12, 5, 1, 9, 2};
BinarySortTree binarySortTree = new BinarySortTree();
//Loop to add nodes to binary sort tree
for (int i = 0; i < arr.length; i++) {
binarySortTree.add(new Node(arr[i]));
}
//Middle order traversal binary sort tree
binarySortTree.infixOrder();//1 3 5 7 9 10 12
//Test delete leaf node
binarySortTree.delNode(2);
binarySortTree.delNode(5);
binarySortTree.delNode(9);
binarySortTree.delNode(2);
binarySortTree.delNode(12);
binarySortTree.delNode(7);
binarySortTree.delNode(3);
//binarySortTree.delNode(10);
//binarySortTree.delNode(1);
System.out.println("After deleting a node");
binarySortTree.infixOrder();
}
}
//Create a binary sort tree
class BinarySortTree {
private Node root;
//Add node method
public void add(Node node) {
if (root == null) {
root = node; //If root is empty, point root directly to node
} else {
root.add(node);
}
}
//Find the node to delete
public Node search(int value) {
if (root == null) {
return null;
} else {
return root.search(value);
}
}
//Find the parent node to delete
public Node searchParent(int value) {
if (root == null) {
return null;
} else {
return root.searchParent(value);
}
}
/**
* Writing method
* 1.Returns the value of the smallest node of a binary sort tree with node as the root node
* 2.Delete the smallest node of the binary sort tree whose node is the root node
* @param node Incoming node (the root node of the current binary sort tree)
* @return Returns the value of the smallest node of a binary sort tree with node as the root node
*/
public int delRightTreeMin(Node node){
Node target=node;
//Loop to find the left child node, and the minimum value will be found
while (target.left!=null){
target=target.left;
}
//This is the target, which points to the smallest node
//Delete minimum node
delNode(target.value);
return target.value;
}
//Delete Vertex
public void delNode(int value) {
if (root == null) {
return;
} else {
//1. You need to find the targetNode to delete first
Node targetNode = search(value);
//If the node to be deleted is not found
if (targetNode == null) {
return;
}
//If we find that the current binary sort tree has only one node
if (root.left == null && root.right == null) {
root = null;
return;
}
//To find the parent node of targetNode
Node parent = searchParent(value);
//If the node to be deleted is a leaf node
if (targetNode.left == null && targetNode.right == null) {
//Judge whether the targetNode is the left child node or the right child node of the parent node
if (parent.left != null && parent.left.value == value) {//Description: targetNode is the left child node of parent
parent.left = null;
} else if (parent.right != null && parent.right.value == value) {//Description: targetNode is the right child node of parent
parent.right = null;
}
} else if (targetNode.left != null && targetNode.right != null) { //Delete a node with two subtrees
int minValue = delRightTreeMin(targetNode.right);
targetNode.value=minValue;
} else { //Delete nodes with only one subtree
//If the node to be deleted has a left child node
if (targetNode.left != null) {
if (parent!=null) {
//If the targetNode is the left child node of the parent
if (parent.left.value == value) {
parent.left = targetNode.left;
} else { //Description: targetNode is the right child node of parent
parent.right = targetNode.left;
}
}else {
root=targetNode.left;
}
} else {//If the node to be deleted has a right child node
if (parent!=null) {
if (parent.left.value == value) { //targetNode is the left child node of parent
parent.left = targetNode.right;
} else { //targetNode is the right child node of the parent
parent.right = targetNode.right;
}
}else {
root=targetNode.right;
}
}
}
}
}
//Medium order traversal
public void infixOrder() {
if (root != null) {
root.infixOrder();
} else {
System.out.println("Binary sort tree is null,Unable to traverse");
}
}
}
//Create Node
class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
//Add node
//Add nodes in the form of recursion. Note that it needs to meet the binary sort tree
public void add(Node node) {
if (node == null) {
return;
}
//Judge the relationship between the value of the incoming node and the value of the root node of the current subtree
if (node.value < this.value) {
//Judge whether the left child node of the current node is null
if (this.left == null) {
this.left = node;
} else {
//Recursively add to the left subtree
this.left.add(node);
}
} else { //The value of the added node is greater than the value of the current node
//Judge whether the right child node of the current node is null
if (this.right == null) {
this.right = node;
} else {
//Recursive right subtree addition
this.right.add(node);
}
}
}
/**
* Find the node to delete
*
* @param value The value of the node you want to delete
* @return If the node is found, the node is returned; otherwise, null is returned
*/
public Node search(int value) {
if (value == this.value) { //This node is found
return this;
} else if (value < this.value) { //If the search value is less than the current node, the left subtree will be searched recursively
if (this.left == null) {
return null;
}
return this.left.search(value);
} else { //If the search value is not less than the current node, recursively search the right subtree
if (this.right == null) {
return null;
}
return this.right.search(value);
}
}
/**
* Find the parent node of the node to delete
*
* @param value The value of the node to find
* @return Return the parent node of the node to be deleted. If there is no parent node, return null
*/
public Node searchParent(int value) {
//If the current node is the parent node of the node to be deleted, it will be reversed
if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
return this;
} else {
//If the searched value is less than the value of the current node, and the left child node of the current node is not null
if (this.left != null && value < this.value) {
return this.left.searchParent(value);//Left subtree recursive lookup
} else if (value >= this.value && this.right != null) {
return this.right.searchParent(value);//Recursive search of right subtree
} else {
return null;
}
}
}
//Medium order traversal
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if (this.right != null) {
this.right.infixOrder();
}
}
}
balanced binary tree
Elicit concepts
Look at a case (to illustrate the possible problems of binary sort tree)
Give you a sequence {1,2,3,4,5,6}, ask to create a binary sort tree (BST), and analyze the problem
The following is the problem analysis of BST:
1) The left subtree is empty, which is more like a single linked list
2) Insertion speed has no effect
3) The query speed is significantly reduced (because it needs to be compared in turn), and the advantages of BST cannot be brought into play, because the left subtree needs to be compared every time, and its query speed is slower than that of the single linked list
4) Solution - balanced binary tree (AVL)

Basic introduction
1) Balanced binary tree is also called self balancing binary search tree, also known as AVL tree, which can ensure high query efficiency.
2) It has the following characteristics: it is an empty tree or the absolute value of the height difference between its left and right subtrees does not exceed 1, and both the left and right subtrees are a balanced binary tree. The common implementation methods of balanced binary tree include red black tree), AVL, scapegoat tree, tree, extension tree, etc.
Left rotation
- Requirements: give you a sequence of numbers to create the corresponding balanced binary tree Sequence {4,3,6,5,7,8}

Right rotation
- Requirements: give you a sequence of numbers to create the corresponding balanced binary tree Sequence {10,12,8,9,7,6}

Double rotation
For the first two sequences, a single rotation (i.e. one rotation) can convert an unbalanced binary tree into a balanced binary tree, but in some cases, a single rotation cannot complete the conversion of a balanced binary tree. Like a sequence
int[] arr = { 10, 11, 7, 6, 8, 9 }; Running the original code, you can see that it is not converted to AVL tree
int[] arr = {2,1,6,5,7,3}; // Running the original code, you can see that it is not converted to AVL tree

Code display
package demo01;
public class AVLTreeDemo {
public static void main(String[] args) {
//int[] arr={4,3,6,5,7,8};
//int[] arr={10,12,8,9,7,6};
int[] arr={10,11,7,6,8,9};
//Create an AVLTree object
AVLTree avlTree = new AVLTree();
//Add node
for (int i = 0; i < arr.length; i++) {
avlTree.add(new Node(arr[i]));
}
//ergodic
System.out.println("Medium order traversal");
avlTree.infixOrder();
System.out.println("After balance treatment~~");
System.out.println("Tree height"+avlTree.getRoot().height()); //3
System.out.println("Height of the left subtree of the tree"+avlTree.getRoot().leftHeight()); //2
System.out.println("Height of right subtree of tree"+avlTree.getRoot().rightHeight()); //2
System.out.println("The current root node is"+avlTree.getRoot()); //8
System.out.println("The left child node of the current root node is"+avlTree.getRoot().left); //7
System.out.println("The right child node of the current root node is"+avlTree.getRoot().right); //10
}
}
//Create AVL tree
class AVLTree {
private Node root;
public Node getRoot() {
return root;
}
//Add node method
public void add(Node node) {
if (root == null) {
root = node; //If root is empty, point root directly to node
} else {
root.add(node);
}
}
//Find the node to delete
public Node search(int value) {
if (root == null) {
return null;
} else {
return root.search(value);
}
}
//Find the parent node to delete
public Node searchParent(int value) {
if (root == null) {
return null;
} else {
return root.searchParent(value);
}
}
/**
* Writing method
* 1.Returns the value of the smallest node of a binary sort tree with node as the root node
* 2.Delete the smallest node of the binary sort tree whose node is the root node
*
* @param node Incoming node (the root node of the current binary sort tree)
* @return Returns the value of the smallest node of a binary sort tree with node as the root node
*/
public int delRightTreeMin(Node node) {
Node target = node;
//Loop to find the left child node, and the minimum value will be found
while (target.left != null) {
target = target.left;
}
//This is the target, which points to the smallest node
//Delete minimum node
delNode(target.value);
return target.value;
}
//Delete Vertex
public void delNode(int value) {
if (root == null) {
return;
} else {
//1. You need to find the targetNode to delete first
Node targetNode = search(value);
//If the node to be deleted is not found
if (targetNode == null) {
return;
}
//If we find that the current binary sort tree has only one node
if (root.left == null && root.right == null) {
root = null;
return;
}
//To find the parent node of targetNode
Node parent = searchParent(value);
//If the node to be deleted is a leaf node
if (targetNode.left == null && targetNode.right == null) {
//Judge whether the targetNode is the left child node or the right child node of the parent node
if (parent.left != null && parent.left.value == value) {//Description: targetNode is the left child node of parent
parent.left = null;
} else if (parent.right != null && parent.right.value == value) {//Description: targetNode is the right child node of parent
parent.right = null;
}
} else if (targetNode.left != null && targetNode.right != null) { //Delete a node with two subtrees
int minValue = delRightTreeMin(targetNode.right);
targetNode.value = minValue;
} else { //Delete nodes with only one subtree
//If the node to be deleted has a left child node
if (targetNode.left != null) {
if (parent != null) {
//If the targetNode is the left child node of the parent
if (parent.left.value == value) {
parent.left = targetNode.left;
} else { //Description: targetNode is the right child node of parent
parent.right = targetNode.left;
}
} else {
root = targetNode.left;
}
} else {//If the node to be deleted has a right child node
if (parent != null) {
if (parent.left.value == value) { //targetNode is the left child node of parent
parent.left = targetNode.right;
} else { //targetNode is the right child node of the parent
parent.right = targetNode.right;
}
} else {
root = targetNode.right;
}
}
}
}
}
//Medium order traversal
public void infixOrder() {
if (root != null) {
root.infixOrder();
} else {
System.out.println("Binary sort tree is null,Unable to traverse");
}
}
}
//Create Node
class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
//Returns the height of the left subtree
public int leftHeight() {
if (left == null) {
return 0;
}
return left.height();
}
//Returns the height of the right subtree
public int rightHeight() {
if (right == null) {
return 0;
}
return right.height();
}
//Returns the height of the current node, which is the height of the tree with the root node
public int height() {
return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;
}
//Method of left rotation
private void leftRotate(){
//Create a new node to the value of the current root node
Node newNode = new Node(value);
//Set the left subtree of the new node as the left subtree of the current node
newNode.left=left;
//Set the right subtree of the new node as the left subtree of the right subtree of the current node
newNode.right=right.left;
//Replace the value of the current node with the value of the right child node
value=right.value;
//Set the right subtree of the current node as the right subtree of the right subtree of the current node
right=right.right;
//Set the left subtree (left child node) of the current node as a new node
left=newNode;
}
//Right rotation method
private void rightRotate(){
//Create a new node to the value of the current root node
Node newNode = new Node(value);
//Set the right subtree of the new node as the right subtree of the current node
newNode.right=right;
//Set the left subtree of the new node as the right subtree of the left subtree of the current node
newNode.left=left.right;
//Replace the value of the current node with the value of the left child node
value=left.value;
//Set the left subtree of the current node as the left subtree of the left subtree of the current node
left=left.left;
//Set the right subtree (right child node) of the current node as a new node
right=newNode;
}
//Add node
//Add nodes in the form of recursion. Note that it needs to meet the binary sort tree
public void add(Node node) {
if (node == null) {
return;
}
//Judge the relationship between the value of the incoming node and the value of the root node of the current subtree
if (node.value < this.value) {
//Judge whether the left child node of the current node is null
if (this.left == null) {
this.left = node;
} else {
//Recursively add to the left subtree
this.left.add(node);
}
} else { //The value of the added node is greater than the value of the current node
//Judge whether the right child node of the current node is null
if (this.right == null) {
this.right = node;
} else {
//Recursive right subtree addition
this.right.add(node);
}
}
//Double rotation
//After adding a node, if it is found that: (right subtree height - left subtree height) > 1, the left rotation is realized
if (rightHeight()-leftHeight()>1){
//If the height of the left subtree of its right subtree is greater than the height of the right subtree of its right subtree
if (right!=null && right.leftHeight()>right.rightHeight()){
//First, rotate the right child node (right subtree) to the right
right.leftRotate();
//Then rotate the current node to the left
leftRotate();
}else {
//Direct left rotation
leftRotate();
}
//Must be!!!!!!!!!!!!
return;
}
//Double rotation
//After adding a node, if it is found that: (left subtree height - right subtree height) > 1, the right rotation is realized
if (leftHeight()-rightHeight()>1){
//If the right subtree height of its left subtree is greater than the left subtree height of its left subtree
if (left!=null && left.rightHeight()>left.leftHeight()){
//First rotate the left child node (left subtree) of the current node - > left
left.leftRotate();
//Then right rotate the current node
rightRotate();
}else {
//Just rotate right
rightRotate();
}
return;
}
}
/**
* Find the node to delete
*
* @param value The value of the node you want to delete
* @return If the node is found, the node is returned; otherwise, null is returned
*/
public Node search(int value) {
if (value == this.value) { //This node is found
return this;
} else if (value < this.value) { //If the search value is less than the current node, the left subtree will be searched recursively
if (this.left == null) {
return null;
}
return this.left.search(value);
} else { //If the search value is not less than the current node, recursively search the right subtree
if (this.right == null) {
return null;
}
return this.right.search(value);
}
}
/**
* Find the parent node of the node to delete
*
* @param value The value of the node to find
* @return Return the parent node of the node to be deleted. If there is no parent node, return null
*/
public Node searchParent(int value) {
//If the current node is the parent node of the node to be deleted, it will be reversed
if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
return this;
} else {
//If the searched value is less than the value of the current node, and the left child node of the current node is not null
if (this.left != null && value < this.value) {
return this.left.searchParent(value);//Left subtree recursive lookup
} else if (value >= this.value && this.right != null) {
return this.right.searchParent(value);//Recursive search of right subtree
} else {
return null;
}
}
}
//Medium order traversal
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if (this.right != null) {
this.right.infixOrder();
}
}
}